Unidade Curricular

Pretende-se que os alunos dominem efetivamente os conceitos e técnicas fundamentais da computação gráfica 2D e 3D.

Para os gráficos 2D são desenvolvidos temas como primitivas de desenho procedimental e gráficos vetoriais, transformações e técnicas de animação. Nos gráficos 3D são tratados os grafos de cena, pontos de vista, geometria e aspeto, transformações, iluminação e animação.

Os conceitos e técnicas são transmitidos no contexto da web, usando as tecnologias mais recentes deste domínio.

• Programa
• Avaliação
• Bibliografia

Usos de IA e outros Sistemas Informáticos

1. É encorajado o uso de sistemas de IA nesta unidade curricular como apoio técnico, analítico e de aprendizagem.
2. É aconselhada uma atitude cética, analítica e inquiridora em relação aos resultados obtidos por esses sistemas:
   • “Isto está certo?”,
   • “Como e porque é que funciona?”,
   • “Quais são as partes importantes?”
   • “E agora, já consigo fazer isto por mim, sem este apoio?”
3. Todas as respostas e todos os trabalhos são sempre da responsabilidade exclusiva e total do aluno que os apresenta.

Programa

Avaliação

• A avaliação de Computação Gráfica tem uma componente teórica e uma componente prática.
• A componente teórica pode ser realizada por exame, ou por testes (ie frequências).
• A componente prática consiste na realização de quatro trabalhos dentro do processo e condições indicadas a seguir.
• Os exames correspondem apenas à componente teórica da avaliação.
• Se reprovar no exame normal pode fazer o exame de recurso.
• Veja as datas das provas nos anúncios do moodle.

Provas Orais — Em casos individuais que o docente ache necessário, pode ser realizada uma prova oral.

Componente Teórica

• A componente teórica vale 60% da nota final (12 valores).
• Cada teste vale 20% da nota final (4 valores).
• Pode realizar os testes que desejar e também os exames (normal e de recurso).
• A nota final desta componente é a combinação mais vantajosa que resulta dos testes e dos exames.
• Exemplo 01. Testes: 03, 03, NA; Exame: 11; Nota final: 11.
• Exemplo 02. Testes: 04, 03, 03; Exame: 08; Nota final: 10.
• Exemplo 03. Testes: 04, NA, 04; Exame: NA; Nota final: 08.

Componente Prática

• A componente prática vale 40% da nota final (8 valores).
• Cada trabalho conta 10% da nota final (2 valores).
• Cada trabalho corresponde a uma das tecnologias: SVG, C2D, X3D e 3JS.
• A componente prática não tem «recurso».
• A classificação de cada trabalho é calculada segundo os Critérios de Avaliação dos Trabalhos Práticos.

Todos os trabalhos terão de ser entregues até à data do «Exame Normal».

Critérios de Avaliação dos Trabalhos Práticos

Note bem o peso de cada componente da avaliação!

Aviso sobre Plágio ou Fraude

1. A fraude ou plágio cometidos em qualquer elemento de avaliação implica a anulação da prova e do seu resultado, sem prejuízo de eventual instauração de procedimento disciplinar.

2. São sanções aplicáveis às infrações disciplinares dos estudantes, de acordo com a sua gravidade:

   1. A advertência;
   2. A multa;
   3. A suspensão temporária das atividades escolares;
   4. A suspensão da avaliação escolar durante um ano;
   5. A interdição da frequência da instituição até cinco anos.

Referências

• Regulamento Académico da Universidade de Évora
• Regime jurídico das instituições de ensino superior
• Regulamento Disciplinar dos Estudantes da Universidade de Évora

Bibliografia

• João Madeiras Pereira, João Brisson, António Coelho, Alfredo Ferreira, Mário Rui Gomes - Introdução à Computação Gráfica (2019).
• Marschner, S., Shirley, P. - Fundamentals of Computer Graphics (2016).
• Hughes J.F., et al. - Computer graphics. Principles and practice (2014).
• Ammeraal, L., Zhang, K. - Computer Graphics for Java Programmers (2007).

Introdução

Conceitos Fundamentais

Processo da Computação Gráfica

• Modelação: Especificação do modelo gráfico.
  • Grafo de Cena: Estrutura de dados que define e organiza o modelo gráfico.
  • Programação gráfica: Uso de uma linguagem de programação, ou um documento, para descrever o grafo de cena.
• Construção: Transformação do modelo gráfico numa imagem.

Definição e Disciplinas Relacionadas.

• Computação Gráfica: É o estudo e aplicação das técnicas de modelação, processamento e construção de objetos gráficos em computadores.
• Visão Artificial: É o oposto da computação gráfica: procura reconstruir um modelo (virtual) a partir de imagens reais.
• Programação de Jogos: É uma aplicação da computação gráfica: usa um modelo (virtual) onde o utilizador interage.
• Processamento de Imagem: Tem técnicas para:
  • Melhoramento de imagem (equalização do histograma, etc).
  • Compressão de imagem.
  • Deteção de features: arestas,super-pixeis, etc..
  • Resolver crimes (CSI).
• Álgebra Linear: Proporciona as bases formais e numéricas para a CG.

Modelação

A modelação consiste em especificar o modelo gráfico que define a imagem.

• Espaço do Modelo: É um espaço 2D ou 3D onde é definido o modelo, juntando e organizando vários objetos gráficos - nos espaços 3D os problemas são mais complexos e tratados de forma significativamente diferente dos espaços 2D.

• Objetos Gráficos: Entidades geométricas (linhas, superfícies) ou luzes, textos, imagens.

• Representações Matemáticas: Permitem definir e transformar os objetos gráficos.

• Vistas: Mostram um modelo numa perspetiva específica e enquadram o passo da construção

  • Os modelos 2D têm vistas relativamente simples.
  • Para modelos 3D é necessário ter em conta inúmeras propriedades que envolvem a câmara, a iluminação, entre outras.

Grafo de Cena

O Grafo de Cena é a estrutura de dados que define o modelo gráfico.

---
config:
  theme: neutral
---
flowchart TD;
scene([scene]) --> person([person])
person --> head([head])
person --> body([body])
person --> arms([arms])
person --> legs([legs])
head --> leye([left eye])
head --> reye([right eye])
head --> mouth([mouth])

arms --> larm([left arm])
arms --> rarm([right arm])

legs --> lleg([left leg])
legs --> rleg([right leg])

Além do “simples” desenho de objetos, interessa definir um modelo onde os objetos são colocados e geridos. O grafo de cena organiza os vários objetos gráficos numa única estrutura de dados que “alimenta” a rotina de rendering.

Programação Gráfica

A programação gráfica consiste em especificar um modelo (i.e. um grafo de cena), usando um programa ou um documento.

• Iniciar o modelo:

  • Colocar e ligar objetos gráficos.
  • Definir vistas.

• Evoluir o modelo:

  • Remover e/ou acrescentar novos objetos.
  • Alterar atributos (posições, …).

Construção

Construção (ou Rendering) é o processo computacional que transforma um modelo gráfico numa imagem exibida num dispositivo físico.

A construção pode ser feita de dois “modos” distintos:

• Modo Retido: O modelo é definido e depois a imagem é construída.
• Modo Imediato: Os objetos são imediatamente desenhados.

Outros Aspetos da Computação Gráfica

• Problemas:

  • Oclusão: o que está “à frente” e o que “fica tapado”?
  • Colocação: posição, rotação, tamanho.
  • Aspeto: cores, texturas, iluminação, sombras.
  • etc.

• Hardware: Ecrãs, Impressoras, Plotters, Projetores holográficos, etc.

• Animação:

  • Filmes: uma sequência de imagens.
  • Jogos: uma sequência de imagens, com interação.
  • Simulações: uma sequência de imagens, seguindo as “leis de um sistema”.

• Interação: Teclados e Ratos, Rede, Interfaces Gráficos, etc.

Aplicações

Filmes

Filme “Avatar”

Jogos

Jogo “Starcraft”

Visualização

Fractal

Simulação

Aerodinâmica

Estatística

Gapminder

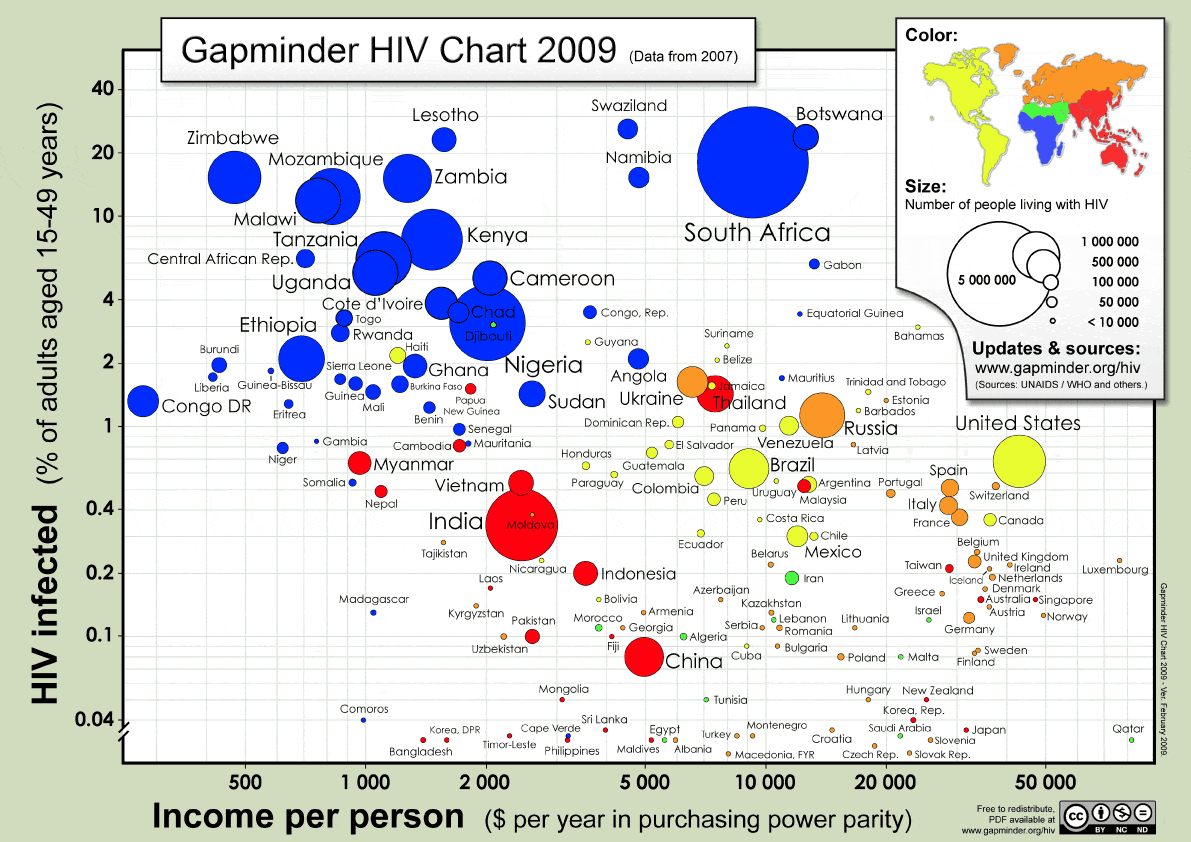
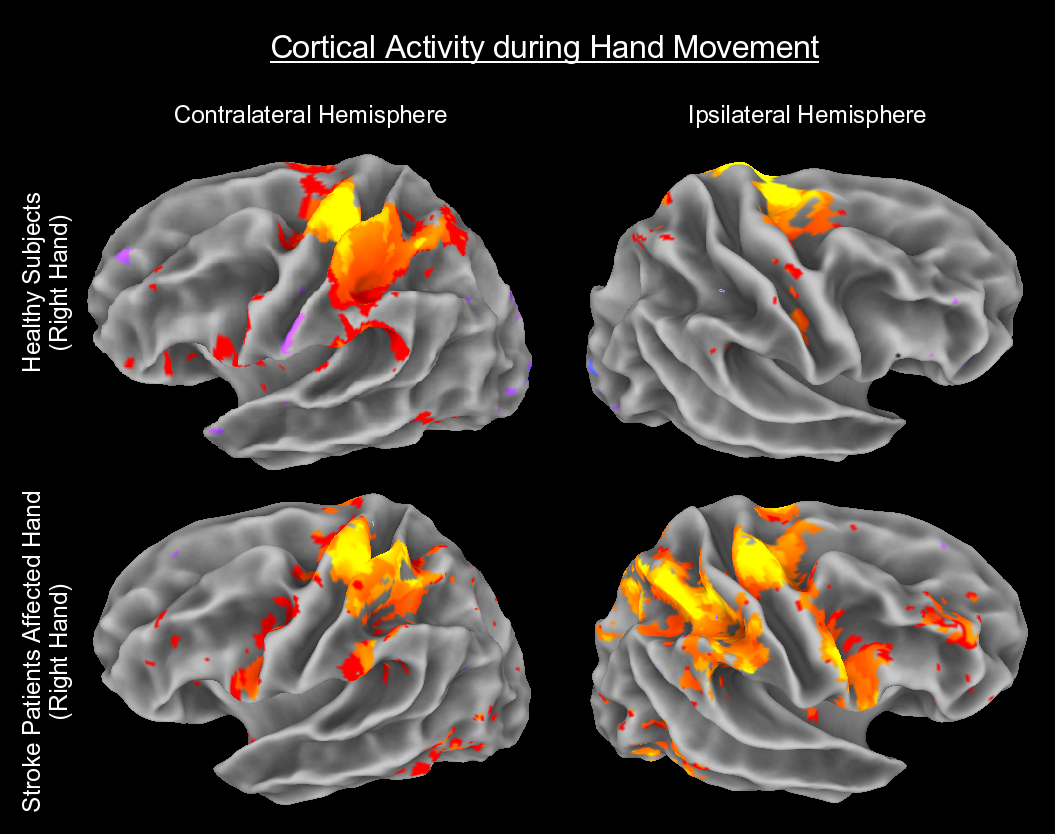
Medicina

Ressonância Magnética

Computação Gráfica na Web

A Computação Gráfica na web proporciona:

• Normas Abertas com ecossistema enorme:
  • Aplicações, Ferramentas.
  • Informação, Comunidade.
• Paradigmas modernos de descrição de dados e de programação.
• Suporte para gráficos 2D (canvas, svg, etc) e 3D (x3dom, three.js, etc).

Web 2D

Os elementos canvas e svg:

• São elementos HTML para gráficos 2D (e 3D).

• Proporcionam ferramentas para modelar:

  • Figuras Geométricas, Texto, Imagens.
  • Transparências, Gradientes, Transformações, Glifos.

Web 3D

• O elemento x3d é usado para integrar conteúdo 3D diretamente num documento html, sem extensões.
• A biblioteca threejs usa o elemento canvas com contexto webgl permite o rendering de gráficos 2D e 3D, sem extensões.

Exemplos elementares

Contexto 2D

<canvas id="cg:exemplos:c2d" width="256" height="128" />
<script>
  const gc = document.getElementById("cg:exemplos:c2d").getContext("2d");
  gc.fillStyle = "steelblue";
  gc.fillRect(64, 32, 128, 64);
</script>

SVG

<svg
    width = "256"
    height = "128">
  <rect
    x = "64" y = "32"
    width = "128" height = "64"
    style = "fill:steelblue"></rect>
</svg>

ThreeJS

<div id="gc:exemplos:3js"></div>
<script>
import * as THREE from 'three';
import { OrbitControls } from 'three/addons/controls/OrbitControls.js';
const renderer = new THREE.WebGLRenderer( {alpha: true} );
renderer.setSize(256, 256);
renderer.setClearColor( 0xffffff, 0);
const container = document.getElementById("gc:exemplos:3js")
container.appendChild(renderer.domElement);
const scene = new THREE.Scene();
const camera = new THREE.PerspectiveCamera(
  35,       // abertura
  500/500,  // proporção largura/altura
  0.1,      // corte perto
  10000     // corte longe
  );
camera.position.set( -2.5, 0, 20 );
camera.lookAt( scene.position );
const geometry = new THREE.BoxGeometry( 5, 5, 5 );
const material = new THREE.MeshLambertMaterial( {color: "steelblue"} );
const mesh = new THREE.Mesh( geometry, material );
scene.add( mesh );
const light = new THREE.AmbientLight( "white" );
scene.add( light );
function animate() {
    mesh.rotation.x += 0.005;
    mesh.rotation.y += 0.005;
    renderer.render(scene, camera);
    requestAnimationFrame(animate);
}
animate();
</script>

X3D

<X3D
    width = "256px"
    height = "256px">
  <Scene>
    <Shape>
      <Appearance>
        <TwoSidedMaterial
          diffuseColor = "steelblue">
        </TwoSidedMaterial>
      </Appearance>
      <Box></Box>
    </Shape>
  </Scene>
</X3D>

Gráficos 2D

Clown, Cavalo, Salamandra, Amadeu de Souza Cardoso

Conceitos Fundamentais 2D

Na computação gráfica 2D, tanto os espaços dos objetos (onde são definidos os objetos gráficos) como o espaço do modelo (onde é definido o modelo) são 2D (isto é, planos).

Modelação. O processo de modelação é relativamente simples:

1. Cada objeto gráfico é definido (pela a sua geometria e outras propriedades não-geométricas, como a cor) no seu próprio espaço do objeto.
2. O modelo é constituído juntando e organizando os vários objetos gráficos já definidos num grafo de cena.

Modelação de Objetos Gráficos

• Geometria (forma). A geometria de um objeto gráfico (2D ou 3D) é geralmente obtida com:

  • Objetos básicos como retas, quadrados, círculos, caminhos ou cubos, cilindros, reticulados, etc.
  • Textos.

• Transformações. As transformações são usadas para:

  • Construir objetos gráficos compostos a partir de outros, mais simples.
  • Posicionar cada objeto gráfico (definido no seu próprio espaço do objeto) no espaço do modelo.
  • Modificar a geometria de objetos usando:
    • Rotações.
    • Escalas.
    • Translações.
    • e outras operações.

• Aspeto (propriedades não geométricas). Além da construção da geometria (isto é, da forma) também são usadas propriedades que dizem respeito ao aspeto:

  • Cores e transparências.
  • Texturas.
  • Estilos de linhas.

Geometria 2D

A geometria dos objetos gráficos usa linhas e outros conjuntos de pontos, como polígonos ou elipses.

O problema que se coloca aqui é saber como representar essas linhas, conjuntos de pontos, etc.

A representação dos objetos gráficos assenta na aplicação da matemática, em particular da Álgebra Linear e da Geometria Analítica, que proporcionam as definições formais (como ponto, plano, etc) e propriedades relevantes.

Neste capítulo vamos explorar a representação matemática das entidades geométricas:

• Sistemas de coordenadas (ou Referenciais).
• Equações para retas, circunferências e elipses.
• Equações paramétricas.
• Caminhos e formas «irregulares».

Referenciais

Referenciais
Referencial Cartesiano x Referencial Ecrã

Um referencial é a ferramenta matemática que permite representar numericamente espaços geométricos.

Uma vez escolhido um referencial, cada ponto do espaço fica identificado por uma lista de números: as coordenadas desse ponto.

Num espaço 2D as coordenadas têm duas componentes, (x, y) e no espaços 3D têm três componentes (x, y, z).

Podemos escolher diferentes referenciais para tratar problemas diferentes. Dois dos referenciais 2D mais comuns são:

• O referencial cartesiano, normalmente usado na aulas de matemática.
• O referencial do ecrã, normalmente usado em dispositivos gráficos;

Geometrias Primitivas

Algumas geometrias primitivas
Um retângulo e um círculo

Matematicamente, um objeto gráfico, como uma linha reta ou uma circunferência, é um conjunto de pontos.

Ingenuamente, poderíamos pensar em usar (digamos) listas com esses pontos. O problema é que mesmo os objetos gráficos mais simples são formados por infinitos pontos (quantos pontos existem numa linha?).

A solução para representar objetos gráficos consistem em usar equações.

Uma equação tem uma quantidade finita de informação que define um conjunto infinito de pontos.

Por exemplo $(x - 2)^2 + (y + 1)^2 = 9$ é um texto finito que define os infinitos pontos da circunferência de raio $3$ centrada em $(2, -1)$.

Consideremos as equações mais comuns:

• Equações da Reta $$Ax + By + C = 0$$ ou $$X = P + \lambda v$$
• Equação da Circunferência $$(x - x_0)^2 + (y - y_0)^2 = R^2$$
• Equação da Elipse $$\left(\frac{x - x_0}{a}\right)^2 + \left(\frac{y - y_0}{b}\right)^2 = 1$$

Mas:

1. Quantos números são usados para representar uma reta? Quantos pontos estão nessa reta?
2. Porque não se usa, para as retas, a equação mais comum $y = mx + b$?
3. Ainda para a equação da reta, como é que se obtém a equação da reta que passa em dois pontos dados?
   • Solução: Dados dois pontos $A = (x_A, y_A)$ e $B = (x_B, y_B)$ uma equação paramétrica da reta que passa em $A$ e $B$ é $$ X = A + \lambda (B - A) = (x_A, y_A) + \lambda (x_B - x_A, y_B - y_A) $$ Esta equação tem a seguinte propriedade conveniente: $X = A$ quando $\lambda = 0$ e $X = B$ quando $\lambda = 1$.

As equações dadas acima não são a forma mais adequada de trabalhar com objetos gráficos para efeitos da computação gráfica.

Desafio. Como obter $100$ pontos da circunferência $x^2 + y^2 = 3$?

Com equações paramétricas, que indicam explicitamente as coordenadas $(x, y)$ dos pontos do objeto.

• Para a reta: $$ X = P + t v \Rightarrow (x,y) = (P_x, P_y) + t (v_x, v_y) \Rightarrow \left\lbrace \begin{aligned} x &= P_x + t v_x \cr y &= P_y + t v_y \end{aligned}\right. $$

• Para a circunferência: $$ (x - x_0)^2 + (y - y_0)^2 = R^2 \Rightarrow \left\lbrace \begin{aligned} x &= x_0 + R \cos t \cr y &= y_0 + R \sin t \end{aligned} \right. $$

• Para a elipse: $$ \left( \frac{x - x_0}{a} \right)^2 + \left( \frac{y - y_0}{b} \right)^2 = 1 \Rightarrow \left\lbrace \begin{aligned} x &= x_0 + a \cos t \cr y &= y_0 + b \sin t \end{aligned} \right. $$

Equações Paramétricas e Geometria

As equações paramétricas usam um parâmetro (nestes exemplos, a variável $t$) que imaginamos que está a percorrer um certo intervalo (digamos $\left\lbrack 0, 2\pi\right\rbrack$) num certo número de passos ($100$ por exemplo).

Conforme $t$ vai tomando diferentes valores nesse intervalo, vamos também obtendo diferentes valores das coordenadas $(x,y)$ dos pontos que formam a geometria do objeto gráfico.

function parametric_circle(cx, cy, r) {
    return function(t) { return {
        x: cx + r * Math.cos(t),
        y: cy + r * Math.sin(t)
        };
    }
}
const ctx = document.getElementById("2d:geo:parametric").getContext("2d");
const my_circle = parametric_circle(128, 128, 64);
ctx.fillStyle = "steelblue";
const n = 64;
for (let t = 0; t <= n; t++) {
    const angle = t * 2 * Math.PI / n;
    p = my_circle(angle);
    ctx.fillRect(p.x - 2, p.y - 2, 4, 4);
};

Desafio. A equação paramétrica da reta tem um problema: O que acontece quando $B = 0$?

Caminhos

As equações permitem representar eficientemente formas «regulares», mas nem sempre existe uma forma «regular» adequada ao objeto que se pretende construir…​

Os caminhos permitem definir formas «irregulares» que podem ser tratadas como “objetos básicos”.

Uma geometria difícil de representar com equações
Gerada pelo código abaixo

<svg>
    <path
        fill="none"
        stroke="steelblue"
        stroke-width="4"
        stroke-linecap="round"
        fill-rule="evenodd"
        transform="translate(256,128)"
        d="
            M -200 0
            Q 0 -200 200 0
            Q 0 200 -200 0
            M -100 50
            L -100 -50
            L 100 50
            L 100 -50
            L -100 50
            Z
        "/>
</svg>

Pensamos num caminho como (o resultado d)as operações que fazemos com um lápis numa folha de papel:

• traçar um contorno;
• pintar o interior dum contorno;

Traçar o contorno dum caminho

Um contorno é formado por por vários segmentos. Cada segmento é traçado a partir do fim do segmento anterior, como um lápis numa folha de papel.

Tipos de segmentos curvos
Uma curva quadrática x uma curva cúbica

Há quatro tipos básicos de segmentos:

• salto. O lápis salta para uma certa posição.
• linha. O lápis desenha uma reta até uma certa posição.
• curva quadrática. O lápis desenha uma curva, controlada por um ponto, até uma certa posição.
• curva cúbica (ou bezier). O lápis desenha uma curva, controlada por dois pontos, até uma certa posição.

Exemplo da construção do contorno dum caminho, segmento-a-segmento

Pintar o interior dum caminho

Pintar o interior dum caminho (isto é, encher a zona delimitada pelo caminho) é uma tarefa surpreendentemente difícil.

Definido um caminho fechado, como determinar se um dado ponto está dentro ou fora da região delimitada pelo caminho?

Para responder a esta questão é usado um de dois algoritmos (regras) para encher um caminho:

• A regra par-ímpar é mais simples e por isso menos controlável.
• A regra não-zero é mais complexa do que a regra par-ímpar mas permite tirar partido da orientação dos segmentos para definir o interior do caminho.

Ambas as regras funcionam com base no seguinte princípio:

1. O retângulo é «varrido de cima para baixo» por linhas que «andam» da esquerda para a direita.
2. Em cada uma dessas linhas são calculados os pontos que intersectam o caminho.
3. É aplicada uma das regras para determinar quais segmentos limitados por esses pontos são interiores e quais são exteriores ao caminho.

Par-ímpar	Não-zero
	Os segmentos do caminho têm de ser orientados.
Os pontos de interseção são numerados da esquerda para a direita (a começar em zero).	Os pontos de interseção são:
	Positivos (azuis) se o segmento vem pela direita da linha.
	Negativos (vermelhos) se o segmento vem pela esquerda da linha.
Os segmentos interiores estão entre um ponto par (azul) e um ponto ímpar (vermelho).	Os segmentos interiores estão entre pontos com total acumulado não zero (estritamente positivo ou negativo).

Explore o código SVG sobre caminhos

<path id="thePath"
    d="
        M 50 50
        L 90 10
        Q 10 10 10 50
        L 50 50
        C 10 90 90 90 70 50
        Z" />

neste documento

Aspeto 2D

A apresentação de um objeto gráfico, além da forma (definida pela geometria) também depende de outras propriedades visuais:

• cores, traços e tintas;
• textos e fontes;

Cores

A especificação numérica de uma cor depende de um espaço numérico.

Conforme a aplicação do modelo gráfico, certos espaços são mais adequados que outros:

• Para ecrãs, onde a cor é emitida, a escolha mais comum é um espaço RGB onde cada cor fica definida por três componentes (r, g, b) correspondentes a vermelho, verde e azul.
• Para impressão, onde a cor é refletida, usam-se espaços CMY (cião, magenta e amarelo) ou CMYK (cião, magenta, amarelo e preto). A adição do preto resulta da dificuldade de se produzir economicamente o preto com as restantes componentes.
• Para certas aplicações a escolha de uma cor em termos de RGB ou CMY (definidos em função do hardware) pode iludir a perceção humana; Um espaço de cor definido em termos de perceção humana é o HSL (de hue=tom, saturation=saturação e luminosity=luminosidade).

No contexto da web o espaço de cor normal é o RGB; Há imensas formas de especificar concretamente uma cor mas a mais comum é da forma #rrggbb em que rr, gg e bb são números entre 0 e 255 representados em notação hexadecimal. Por exemplo:

Além disso, através do CSS, também estão disponível cores por nome (ver as tabelas de cores na norma w3 ou na wikipedia).

Testar cores HSL

Testar cores RGB

Traços

Os traços (isto é, as propriedades visuais das linhas) são inesperadamente complexos.

Uma linha desenhada num dispositivo não é um objeto abstrato (como uma linha matemática, de espessura 0). Na prática as linhas têm formas específicas.

Os traços são definidos por:

• uma espessura.
• um tracejado
• as extremidades.
• as junções com outros traços.
• o corte das junções.

Exemplos de traços	CSS
Espessuras	stroke-width
	0.15, 1, 2, 4, 8
Tracejados	stroke-dasharray
	2 2, 1 2, 2 1 4 1, 1 2 2 1
Extremidades	stroke-linecap
	butt, round, square
Junções	stroke-linejoin
	miter, round, bevel
Cortes	stroke-miterlimit
	1, 4

Testar traços

Tintas

A tinta define como uma forma é pintada. Há várias formas de pintar uma geometria:

• usando uma cor sólida;
• usando um mosaico (uma imagem repetida);
• usando um gradiente de cores (uma variação suave entre cores);

Uma tinta pode ser aplicada apenas ao contorno (stroke) ou encher (fill) o interior da geometria:

Traçar e Pintar um caminho
Traçar x Pintar

Mosaicos

O uso de mosaicos para traçar ou encher o contorno é semelhante à aplicação de uma cor sólida, com a particularidade de que a «cor» é um padrão repetido:

Tinta do tipo “mosaico”
Traçar x Pintar com mosaicos

Gradientes de Cores

Os gradientes mais simples são lineares: uma cor inicial vai mudando suavemente ao longo de uma linha, até chegar a uma cor final. Também podemos definir versões um pouco mais complexas, com várias cores:

Um gradiente linear

A forma de definir gradientes “multi-coloridos” consiste em associar cores a pontos de paragem. Um ponto de paragem fica definido por um certo offset (deslocamento) do caminho entre o ponto mais à esquerda e o ponto mais à direita:

• o ponto mais à esquerda tem offset 0;
• o ponto mais à direita tem offset 1;
• pontos intermédios têm offset entre 0 e 1. Por exemplo, um ponto exatamente a meio tem offset 0.5 e um ponto a um quarto “do início do caminho” tem offset 0.25;

Por exemplo, o gradiente acima está definido com:

1. Uma paragem com offset 0.00 e cor khaki:

2. Uma paragem com offset 0.20 e cor steelblue:

3. Uma paragem com offset 0.75 e cor crimson:

4. Uma paragem com offset 1.00 e cor darkseagreen:

Outra propriedade que controla a aplicação dos gradientes é o prolongamento, que em geral tem três formas:

Formas de prolongar gradientes
espelho (reflect) x repetir (repeat) x expandir (pad)

Finalmente, um gradiente também pode ser circular (em vez de linear):

Um gradiente circular

Texto

Texto e Fonte

O uso de textos envolve selecionar uma fonte e desenhar o texto de acordo com essa fonte.

• Um texto é um tipo especial de objeto geométrico, definido por uma sequência de carateres (letras, dígitos, etc);
• Uma fonte define os desenhos dos carateres;

Letras, Dígitos, Glifos

Tecnicamente, glifo é o termo que designa, em conjunto:

• As letras (a é β etc).
• Os dígitos (0 1 9 etc).
• Símbolos de pontuação (! , . etc).
• As ligaturas (Æ Œ fi etc).
• Outros símbolos (± ∫ → etc).

As propriedades das fontes estão definidas na norma CSS Fonts Module Level 3 e incluem, entre outras:

Transformações 2D

O processo da computação gráfica determina os seguintes passos:

1. Modelação:
   1. Definição de cada objeto gráfico no respetivo espaço do objeto;
   2. Definição do modelo, no espaço do mundo, juntando os vários objetos gráficos do ponto anterior num único grafo de cena;
2. Construção (Rendering): No espaço do dispositivo, com base no modelo do ponto anterior e das definições da vista;

A construção assenta num conjunto de operações (por exemplo, clipping) que, normalmente, são automaticamente tratadas pelo sistema gráfico em que se está a trabalhar.

Sobre a modelação falta esclarecer:

• Como cada objeto gráfico é definido no seu espaço;
• Como esse objeto é «transportado» para o espaço do mundo;

As Transformações são as principais ferramentas nestes passos. Neste capítulo vamos ilustrar o papel que desempenham.

Transformações: Representação Matricial e Casos Especiais

Uma transformação é uma função que aplica pontos em pontos:

$$ p = (p_x, p_y) \stackrel{T}{\longrightarrow} q = (q_x,q_y) $$

Os tipos principais de transformações são:

• Translação: $q = (q_x,q_y)$ resulta de mover $p = (p_x, p_y)$ segundo uma certa direção;

• Rotação: $q = (q_x,q_y)$ resulta de rodar $p = (p_x, p_y)$ um certo ângulo em torno da origem;p_0 =

• Escala: $q = (q_x,q_y)$ resulta de aumentar ou reduzir $p = (p_x, p_y)$ por um certo fator;

• Composição: $q = (q_x,q_y)$ resulta de aplicar a $p = (p_x, p_y)$ uma sequência de transformações;

Adicionalmente ainda podem ser usadas reflexões (em relação a um certo eixo ou ponto) e deslizamentos (numa certa direção).

A escolha destes quatro tipos de transformações principais assenta nas seguintes razões:

• são suficientemente expressivos para a maior parte das necessidades da computação gráfica;
• são intuitivamente acessíveis;
• são numericamente eficientes;

A eficiência numérica assenta na forma como os cálculos são efetuados: as coordenadas transformadas $(q_x, q_y)$ resultam de multiplicar as coordenadas originais $(p_x,p_y)$ por uma matriz de transformação:

$$ \begin{bmatrix} q_x \cr q_y \cr 1 \end{bmatrix} = \begin{bmatrix} a & b & c \cr d & e & f \cr 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_x \cr p_y \cr 1 \end{bmatrix} $$

Os valores concretos dos parâmetros a,b,c,d,e,f dependem da transformação concreta que se pretende aplicar às coordenadas originais.

Nas páginas seguintes vamos ver como esses valores também dependem do tipo de transformação.

Translações

Exemplo de uma Translação

Uma translação consiste em mover as coordenadas originais $p = (p_x,p_y)$ segundo um certo vetor $d = (d_x, d_y)$ de forma que $$ q = p + d. $$

Isto é, as coordenadas transformadas são obtidas por $$ (q_x, q_y) = q = p + d = (p_x,p_y) + (d_x, d_y) $$

A matriz de translação é

$$ \begin{aligned} T(d_x,d_y) &= \begin{bmatrix} 1 & 0 & d_x \cr 0 & 1 & d_y \cr 0 & 0 & 1 \end{bmatrix} \end{aligned} $$

e temos

$$ \begin{aligned}(q_x, q_y, 1) &= T(d_x,d_y) \begin{bmatrix} p_x\cr p_y \cr 1 \end{bmatrix}\end{aligned} $$

Rotações

Exemplo de uma Rotação

Uma rotação consiste em rodar as coordenadas originais $(p_x, p_y)$ segundo um certo ângulo $\alpha$ em torno da origem $(0, 0)$.

A matriz de rotação é

$$ \begin{aligned} R(\alpha) &= \begin{bmatrix} \cos\alpha & \sin\alpha & 0 \cr -\sin\alpha & \cos\alpha & 0 \cr 0 & 0 & 1 \end{bmatrix} \end{aligned} $$

e temos

$$ \begin{aligned}(q_x,q_y,1) &= R(\alpha) \begin{bmatrix} p_x\cr p_y \cr 1 \end{bmatrix}\end{aligned} $$

Escalas

Exemplo de uma Escala

Uma escala consiste em encolher ou esticar as coordenadas originais $(p_x, p_y)$ segundo um certo fator $(s_x, s_y)$.

A matriz de escala é

$$ \begin{aligned} S(s_x,s_y) &= \begin{bmatrix} s_x & 0 & 0 \cr 0 & s_y & 0 \cr 0 & 0 & 1 \end{bmatrix} \end{aligned} $$

e temos

$$ \begin{aligned}(q_x,q_y,1) &= S(s_x,s_y) \begin{bmatrix} p_x\cr p_y \cr 1 \end{bmatrix}\end{aligned} $$

Composição

Nem sempre as transformações básicas são suficientes para construir os objetos gráficos pretendidos.

Nesse caso é necessário compor as transformações básicas de forma a obter-se o efeito pretendido.

Motivação da composição

Exemplo de uma Composição

Supondo que se pretende escalar e rodar um certo objeto gráfico, sem o deslocar da posição em que está. O problema está na rotação, quo o feita em torno da origem do referencial, e não em torno do «centro do objeto».

A solução consiste em compor várias transformações de forma a obter-se o efeito pretendido. Geometricamente:

1. Colocamos o referencial no «centro» do objeto, com uma translação.
2. Com o referencial no «centro» do objeto, fazemos as operações de escala e de rotação.
3. Repomos o referencial na posição em que estava inicialmente, de novo com uma translação.

Explore o código SVG sobre transformações

neste documento

Gráficos 3D

A Strange World M. C. Escher

Conceitos Fundamentais 3D

A Computação Gráfica 3D trata o problema da visualização a 2D de modelos 3D. Estes são compostos por objetos gráficos, fontes de luz e câmaras.

Um sistema gráfico 3D tem de resolver os muitos problemas derivados da representação dos objetos, das transformações, da organização e da construção da cena.

Funções de um Sistema Gráfico 3D

• Definir a geometria dos objetos gráficos.
• Aplicar transformações geométricas, aos objetos e às câmaras para os localizar e posicionar.
• Definir o aspeto (usando Texturas e Materiais) dos objetos.
• Iluminar a cena.
• Definir a vista (usando propriedades como projeção, localização, atitude, abertura, etc) do modelo.

Geometria 3D

Geometria de um rosto

Tipos de Geometrias

A geometria de um objeto 3D pode ser aproximada por várias técnicas.

Formas Básicas

Cubos, esferas, pirâmides, cones, etc.

As formas básicas são proporcionadas «diretamente» pelo sistema gráfico.

Geometrias Parametrizadas

Um cilindro é o rasto que uma circunferência deixa quando se desloca ao longo de um segmento de reta perpendicular ao plano da circunferência.

Certas formas podem ser definidas por um pequeno conjunto de parâmetros e objetos auxiliares e são proporcionadas por «funções» do sistema gráfico.

Conjuntos de Faces

Um rosto, o relevo de um terreno.

Formas mais irregulares têm de ser construídas definido individualmente as coordenadas dos vértices de uma rede de polígonos.

Além destas formas de construção de geometrias «estáticas» também são usadas técnicas que deformam a geometria inicial e que envolvem «esqueletos» e/ou «morphing». Estes técnicas não constam do programa deste curso.

Geometria construída

A geometria de um barco, construida a partir de proa, uma quilha e uma popa.

A popa e a proa são transformadas para se ajustarem à quilha. A quilha é uma extrusão, a proa é um conjunto de faces e a proa é uma transformação da popa.

Além das formas básicas, em geral estão disponíveis outras métodos para definir a geometria dos objetos gráficos.

Os métodos principais para construir geometrias são:

• As geometrias parametrizadas; em particular, extrusões.
• Os conjuntos de faces.

Exemplo/Aplicação da construção de geometrias.

Vamos ilustrar estes dois métodos construindo um objeto que usa ambos. O casco de um barco tem três partes:

• A proa (bow), usando um conjunto de faces.
• A quilha (keel), com uma extrusão.
• A popa (stern), transformando a proa.

Extrusões

Peças de alumínio feitas por extrusão (fonte: Wikipedia)

A secção transportada ao longo da espinha gera uma geometria 3D :

Exemplos de extrusões

• [2D] Um segmento é o rasto dum ponto quando se movimenta «a direito».
• [2D] Um quadrado é o rasto dum segmento quando se movimenta «a direito»
• [2D] Um círculo é o rasto dum segmento quando roda em torno dum ponto.
• [3D] Um cubo é o rasto dum quadrado ao longo dum segmento.
• [3D] Um cilindro é o rasto duma circunferência ao longo dum segmento.

Parâmetros das extrusões

Uma extrusão é definida por:

• A secção
  • Uma superfície 2D assente no plano Y=0.
  • Por exemplo, uma circunferência, um disco, um «L».
• A espinha
  • Uma sequência de pontos no espaço 3D.
• Parâmetros adicionais
  • Parâmetros específicos de cada sistema gráfico, que controlam pormenores do rendering desta geometria.
  • Por exemplo, no sistema X3D as extrusões podem ter rotações e escalas definidas ao longo da espinha.

Estes parâmetros definem uma geometria de acordo com o seguinte processo:

1. A secção, que é definida no plano Y=0 é «transportada» para o primeiro ponto da espinha e orientada para o ponto seguinte.
2. Da mesma forma, a secção é colocada no segundo ponto da espinha.
3. Os vértices correspondentes da primeira e da segunda secções são ligados, formando um quadrilátero entre cada par de vértices.
4. Este processo é depois repetido para o resto dos pontos da espinha, resultando numa superfície de extrusão («arrasto») ao longo da espinha.

Conjuntos de Faces

Aproximações de uma geometria por conjuntos de faces
fonte: Artigo «Computer Graphics (computer science)» na Wikipédia

Formas pouco regulares (por exemplo, um rosto ou um terreno) têm de ser construídas definido individualmente as coordenadas dos vértices e ligando esses vértices para formar faces (triângulos ou quadriláteros).

Parâmetros dos conjuntos de faces

Um conjunto de faces é definido por:

• Os vértices
  • Um ponto no espaço 3D, dado pelas suas coordenadas x, y, z.
  • Em geral os vértices são «arrumados» numa lista e referenciados pelo seu índice nessa lista.
• As faces
  • Uma lista de três (ou, no caso do X3D, mais) vértices.
  • Normalmente é usado o índice na lista dos vértices, em vez das coordenadas.

Regra da mão direita

Um aspeto importante na definição de uma face é a ordem em que os (índices dos) vértices são dados.

Dados três pontos no espaço 3D, A, B, C, a face «para cima» é definida pela regra da mão direita. Se os pontos forem dados pela ordem A, C, B então a face «para cima» é oposta.

Quando esta regra é esquecida o resultado típico são «faces invisíveis».

Aspeto 3D

Efeito da iluminação na perceção de um objeto

A luz é refletida segundo um certo ângulo tangente à superfície do objeto no ponto onde incide:

• O ângulo é determinado pelas normais (que dependem da geometria do objeto).
• As cores somam a cor própria do objeto à cor da luz incidente.
• Os reflexos definem quanta luz incidente é refletida pelo objeto.

O aspeto percecionado de um objeto depende:

• Da iluminação da cena.
• Da textura desse objeto.

Parâmetros das texturas

As texturas (ou materiais) são propriedades do objeto que contribuem para a sua perceção e definem como o objeto é «pintado» e como transforma a luz.

• Cores (difusão: diffuse)
  • São as cores próprias do objeto: luz refletida = cor do objeto + luz incidente.
  • Por exemplo, um cubo laranja difunde a cor laranja e um cubo verde difunde verde.
• Reflexos (specular)
  • Determinam a quantidade de luz refletida: luz refletida = reflexo _ luz incidente.
  • Por exemplo, um cubo brilhante reflete quase toda a luz que recebe, enquanto que um cubo baço quase não reflete a luz que recebe.
• Normais (normals)
  • Dependem da geometria do objeto e determinam a direção da luz refletida: ângulo da luz refletida = normal + ângulo da luz incidente.
  • Por exemplo, num cubo liso as normais são perpendiculares às faces mas num cubo rugoso as normais têm desvios da perpendicular.

Tipos de iluminação

A iluminação resulta de um conjunto de propriedades do modelo (da cena) que contribuem para a perceção dos vários objetos nesse modelo.

As fontes de Luz definem propriedades como «cor emitida», «atenuação», etc e, em geral, incluem os seguintes tipos:

• Luz Ambiente
  • Incide igualmente em todos os objetos gráficos, independentemente da posição ou pose.
• Ponto de Luz
  • Emite luz em todas as direções, a partir de uma certa posição.
  • Por exemplo, uma lâmpada numa sala.
• Foco
  • Emite um cone de luz (com uma certa orientação) a partir de uma certa posição.
  • Por exemplo, um projetor numa secretária.
• Direcional
  • Emite luz em «raios paralelos» a uma certa orientação.
  • Por exemplo, o sol a iluminar uma cena na superfície da terra.

Mapas de texturas

Não é viável definir-se ponto-a-ponto os parâmetros de textura numa geometria. Em vez disso, usam-se imagens especiais, os mapas de textura, para aplicar cores, reflexos e normais a uma geometria.

Vejamos o efeito que cada caraterística das texturas tem na perceção (e realismo) do objeto seguindo um exemplo: o planeta terra.

Modelo da terra: geometria

A geometria da terra é (aproximadamente) uma esfera, e vamos supor que na cena há um ponto de luz razoavelmente afastado, de forma a simular o sol.

Modelo da terra: difusão

A difusão define as cores «próprias» do objeto: luz refletida = cor do objeto + luz incidente.

Difusão da terra
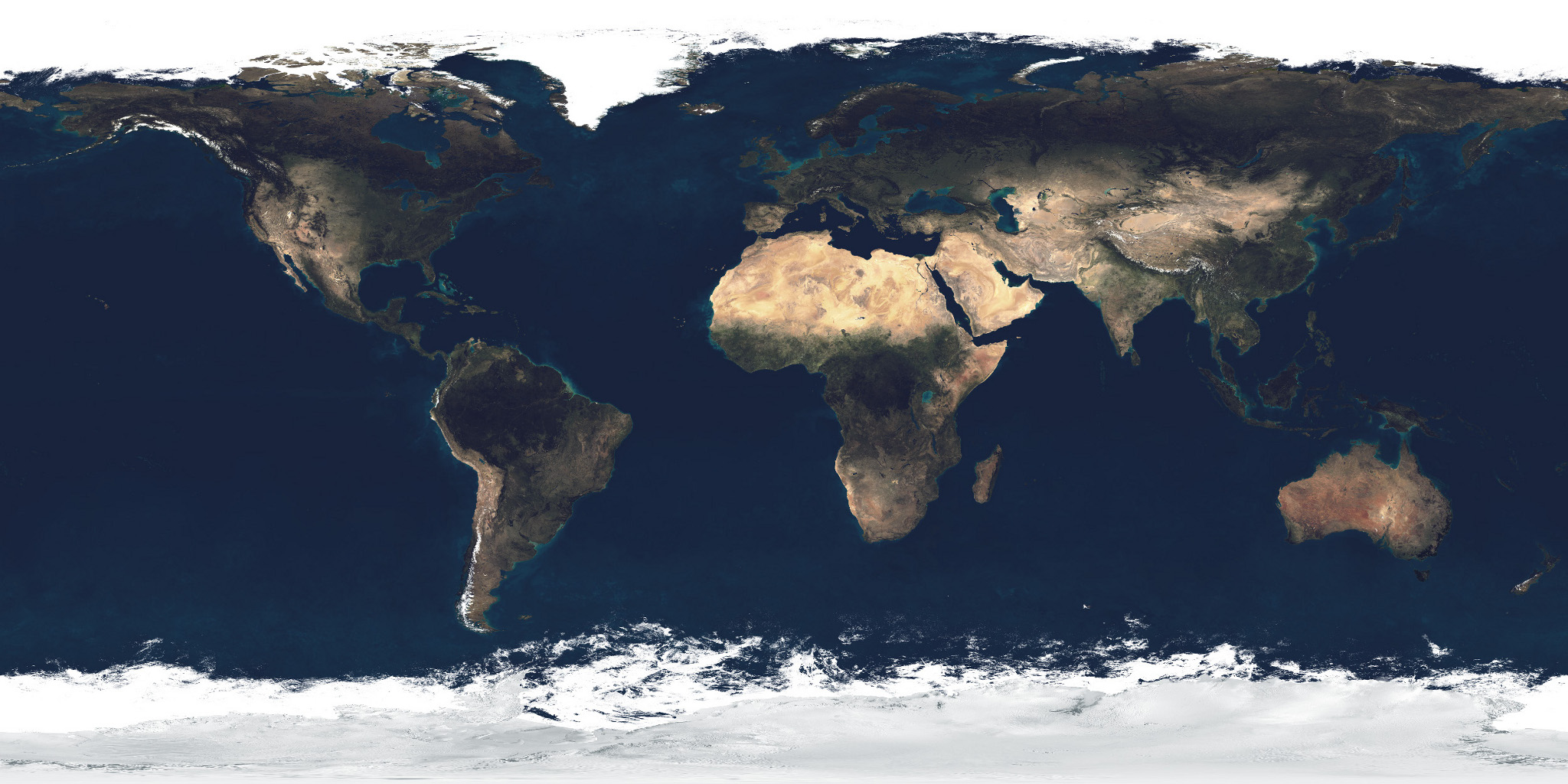Uma imagem com as cores da superfície da terra

Para pintar «num passo» todas as cores da superfície da esfera usa-se uma textura para a difusão das cores.

Modelo da terra: reflexos

Os reflexos determinam a quantidade de luz refletida: luz refletida = reflexo * luz incidente.

Reflexos da terra
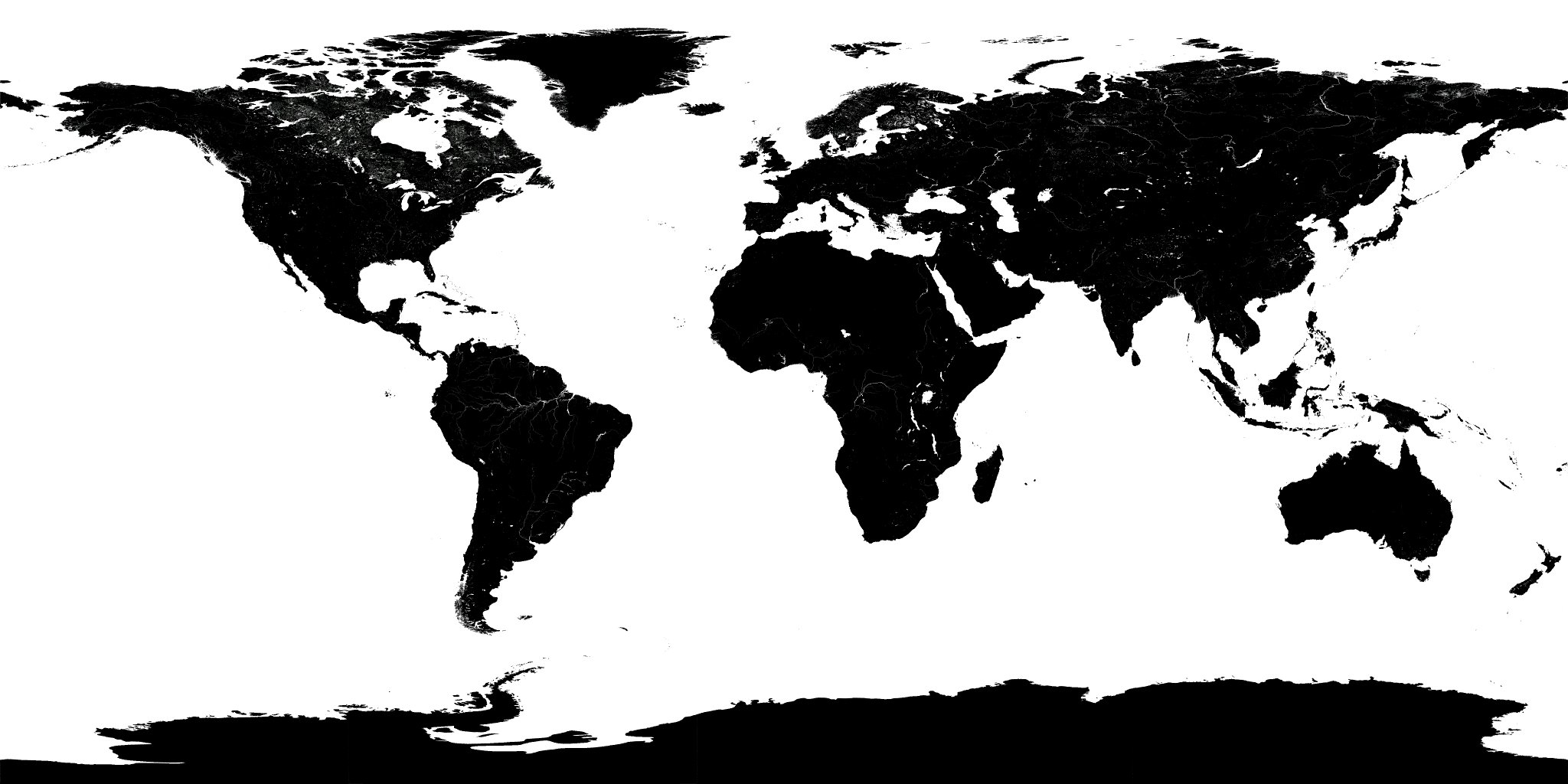Uma imagem com os reflexos da superfície da terra

Para pintar «num passo» todos os reflexos na superfície da esfera usa-se uma textura para a reflexão das cores.

Nestas texturas branco significa «reflete 100%», preto significa «reflete 0%» e tons intermédios refletem percentagens intermédias.

A principal diferença em relação aos mapas de difusão «simples» está nas zonas que devem brilhar. Por exemplo, nas zonas com água (rios, lagos, mares, oceanos) pode ver-se o reflexo do «sol» enquanto que nas zonas «de terra» não há grandes diferenças.

Modelo da terra: normais

As normais determinam a direção da luz refletida: ângulo da luz refletida = normal + ângulo da luz incidente.

Normais da terra
Uma imagem com as normais da superfície da terra

Para pintar «num passo» as normais à superfície da esfera usa-se uma textura para as normais.

Representação das normais por uma imagem

Uma normal é um vetor no espaço 3D e, como tal, tem três componentes, xyz.

Uma cor também tem três componentes, RGB, e nestes mapas uma cor RGB representa um vetor xyz associando: R → x, G → y, B → z.

Mapas UV

A aplicação de uma textura à geometria tem de ser controlada, de forma a aplicar as partes corretas da textura às faces da geometria. Esse controlo é definido por um mapa UV.

Aplicação das texturas por faces

Uma textura para um dado

As texturas definidas por imagens são uma forma conveniente de refinar o aspeto de um objeto gráfico.

Para funcionar corretamente, é preciso controlar como cada setor da textura é associado a cada face da geometria do objeto.

As coordenadas uv são usadas para posicionar os pontos da textura:

• Usa-se «uv» em vez de «xy» para evitar confusões com as coordenadas xyz da geometria.
• O referencial uv é adaptado de forma a que toda a imagem da textura fique no quadrado $(0,0) - (1,1)$.

Pontos e setores de uma textura
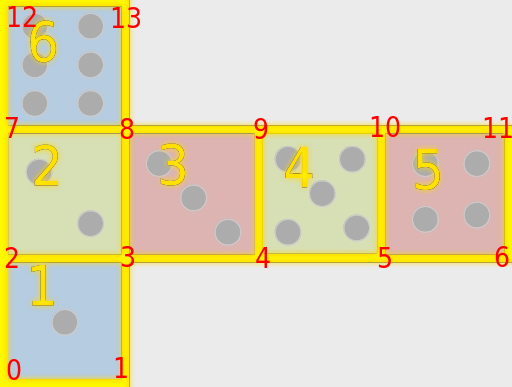Cada setor (amarelo) é definido por pontos uv (vermelhos)
O setor 4 é definido pelos pontos uv 4, 5, 10, e 9
O ponto 0 tem coordenadas uv $(0,0)$; O ponto 9 tem coordenadas uv $(0.5, 0.66)$

Especificamente:

• Os vértices estão na geometria 3D
  • Têm coordenadas xyz.
• As faces estão na geometria 3D
  • Definem-se com listas de índices de vértices.
• Os pontos estão na textura 2D
  • Têm coordenadas uv.
• Os setores são «pedaços» da textura 2D
  • Definem-se com listas de índices dos pontos.

A aplicação de mapas UV é adequado a geometrias definidas por conjunto de faces onde os vértices e as faces estão explicitamente indicados.

Processo para definir um mapa UV

O processo para ilustrar a aplicação dos mapas UV é o seguinte:

1. Definir os vértices e a lista de faces da geometria 3D.
2. Definir os pontos e a lista de setores da textura 2D.
3. O primeiro setor é aplicado à primeira face, etc.

Regra da mão direita. Na definição dos setores, 7 8 3 2 não é o mesmo que 7 8 2 3.

Tem de usar a regra da mão direita para se determinar o lado da face como uma página numa folha de papel.

Transformações 3D

Investigação da perspetiva (gravura de Albrecht Dürer, 1525)
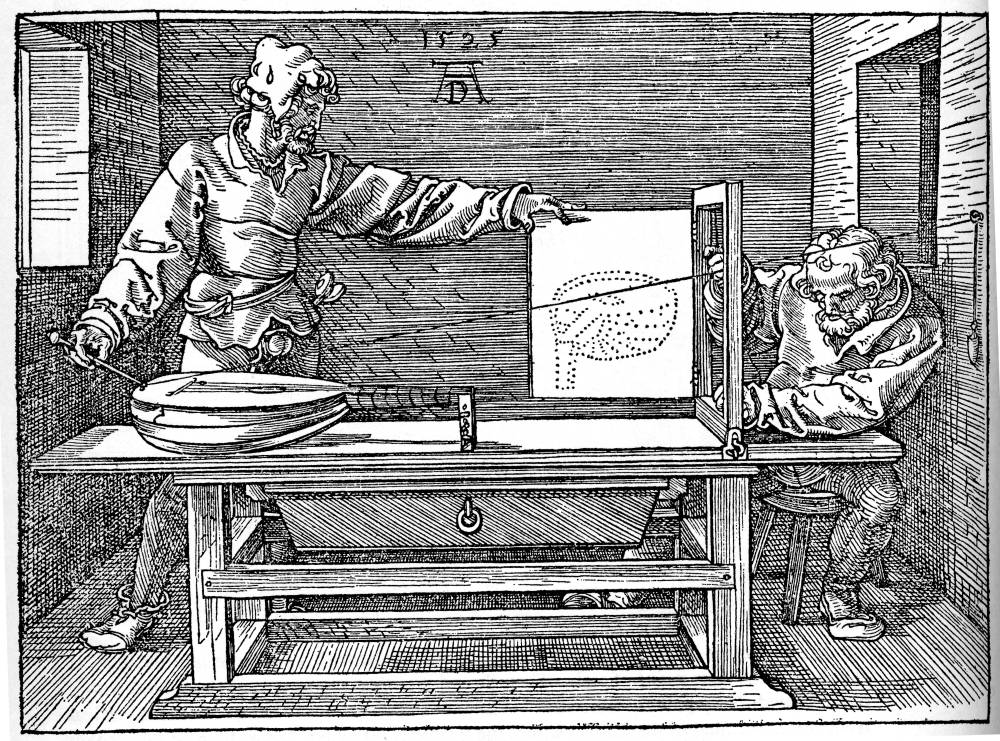Representação 2D de um objecto 3D

São usados dois tipos de transformações num sistema gráfico 3D:

• Transformações afins. Alteram o tamanho, posição e orientação de objectos no espaço 3D.
  • São geralmente usadas no espaço do mundo ou do objeto e generalizam as transformações dos sistemas gráficos 2D. São usadas para posicionar, rodar e escalar os objetos gráficos.
• Projeções. Produzem a vista 2D do modelo 3D.
  • Estão associadas a câmaras e são usadas para definir a vista da cena, isto é, a transformação espaço 3D do modelo → espaço 2D do dispositivo.

Parâmetros de vistas e de câmaras

Uma vista de uma cena é obtida fazendo uma certa projeção do modelo, precisamente da mesma forma que uma câmara fotográfica produz uma imagem 2D de um ambiente 3D.

A projeção que define a vista é normalmente designada câmara e depende de um conjunto de parâmetros. Os mais comuns são:

• Tipo

  • Tipo da projeção (ortográfica, projetiva, etc depende do sistema gráfico).

• Abertura (FOV)

  • Ângulo de captura (depende do tipo de câmara).

• Proporção (Ratio, Aspect)

  • Relação entre a altura e a largura (depende do tipo de câmara).

• Perto (Near)

  • Distância do plano de corte «perto».

• Longe (Far)

  • Distância do plano de corte «longe».

Animação

Estroboscópio
A ilusão de movimento resulta da rapidez com que as imagens são apresentadas

Com animação uma cena estática ganha vida e torna-se mais informativa e interessante.

A animação resulta de mostrar imagens, os fotogramas (em inglês frames) em rápida sucessão: Animação = Imagem x Tempo.

Animação por Fotogramas

Figuras em vaso funerário (3º Milénio AEC)
Imagens sequenciais dum salto de um bode

O número de fotogramas e de FPS são fixos.

Por exemplo: 480 fotogramas a 24 FPS proporcionam uma animação (um filme) com 20 segundos de duração.

O limiar perceção humana anda perto dos 24FPS.

• Se os fotogramas forem substituídos a um ritmo de 24 por segundo, a maioria das pessoas não distingue a passagem de um fotograma para o seguinte e interpreta «o que está a ver» como um movimento fluído.
  • Na realidade, 24 fotogramas por segundo está demasiado perto do limiar de perceção e a esta frequência muitas pessoas apercebem-se da substituição dos fotogramas.
• Os primeiros filmes foram filmados e projetados entre 16FPS e 24FPS.
• A frequência «padrão» 24FPS foi adotado no início da computação gráfica.
• Atualmente as placas gráficas proporcionam facilmente 60+FPS.

Uma animação por fotogramas é feita para uma certo número de FPS e não resulta bem com FPS diferentes.

• O número de FPS pode variar em função do dispositivo, da “carga”, etc.

A animação por tempo resolve o problema das diferenças de frequências na animação por fotogramas.

Animação e Programação

Daqui em diante a matéria de Computação Gráfica muda substancialmente.

O foco deixa os sistemas gráficos específicos e passa para a representação e para o processamento de modelos gráficos.

Certifique-se que está confortável a programar.

Animação por tempo

A animação por tempo resulta de definir chaves (keys): Os valores de certos parâmetros em determinados instantes.

Por exemplo: A posição x = 1 no instante t = 0 e x = 2 no instante t = 2.

É necessário calcular automaticamente os valores intermédios dos parâmetros que controlam uma animação.

Por exemplo:

• A posição de objeto é definida pelo parâmetro x.
• É data a posição inicial: x = 1 quando t = 0.5.
• E a posição final: x = 2 quando t = 2.5.
• Sempre que necessário, pretende-se calcular as posições intermédias desse objeto.

Interpolação linear de valores intermédios entre duas chaves

As chaves definem os pontos «vermelhos»; o início e o fim:

const keys = [
  {
    t: 0.0,
    parameters: {  x: 1.00  }
  },
  {
    t: 2.0,
    parameters: {  x: 2.00  }
  }
];

Valores Interpolados
Os pontos «verdes» são calculados pela interpolação linear entre os pontos «vermelhos».

Processo da Animação por Tempo

1. São definidas chaves (keys) específicas.

• Cada chave define um instante e valores de parâmetros.

2. Durante a animação:

• Os valores dos parâmetros são recalculados sempre que necessário.
• O modelo gráfico é atualizado com os novos valores dos parâmetros e construído/desenhado de novo.

A animação por tempo resolve o problema das diferenças de frequências que a animação por fotogramas coloca.

Sempre que o sistema gráfico está pronto para mostrar um novo fotograma, os valores dos parâmetros são recalculados; o modelo gráfico é atualizado com os novos valores dos parâmetros e desenhado de novo.

Isto significa que a definição de uma animação é feita através de modelo e esse modelo tem parâmetros que definem cada «fotograma» na sequência.

Modelos e Parâmetros

• Modelo — Conjunto de variáveis (parâmetros) que definem cada «fotograma» na sequência.
• Parâmetro — Variável que define um elemento da animação.

Exemplos de Modelos e Parâmetros

1. Um quadrado vermelho desloca-se da esquerda para a direita. Neste caso o modelo necessita apenas de um parâmetro, a abcissa ($x$) do quadrado:

   const model = { x: 0 };
   

2. Um quadrado vermelho desloca-se na horizontal e na vertical. O modelo necessita de dois parâmetros, a abcissa ($x$) e a ordenada ($y$) do quadrado:

   const model = { x: 0, y: 0 };
   

3. Um quadrado desloca-se na horizontal, na vertical e pode mudar de cor:

   const model = { x: 0, y: 0, color: 'crimson' };
   

4. Vários quadrados deslocam-se na horizontal, na vertical e podem mudar a cor:

   const model = { my_squares: [
     { x: 0, y: 0, color: 'crimson' },
     { x: 0, y: 8, color: 'khaki' }
   ] };
   

Tweens

Os tweens (contração do inglês «in-between») assentam uma técnica simples mas flexível e eficiente para:

• calcular os valores intermédios entre
• um valor inicial $x_I$ e
• um valor final $x_F$ durante
• um certo intervalo de tempo $[t_I, t_F]$.

O valor intermédio, $x_t$, quando $t_I \leq t \leq t_F$, é calculado usando a fórmula: $$ x_t = \frac{(t_F - t)x_I + (t - t_I)x_F}{t_F - t_I} $$

Um tween atualiza, ao longo de um certo intervalo de tempo $[t_I, t_F]$, um valor $x_t$ que varia de $x_I$ quanto $t = t_I$ para $x_F$ quando $t = t_F$.

Os parâmetros fundamentais de um tween são:

• Valor Inicial ($x_I$)
  • Em que valor começa a variação do parâmetro.
• Valor Final ($x_F$)
  • Em que valor termina a variação do parâmetro.
• Tempo Inicial ($t_I$)
  • Em que instante começa a variação do parâmetro.
• Tempo Final ($t_F$) ou Duração ($d$)
  • Em que instante termina a variação (tempo final) ou quanto tempo demora a variação (duração). A relação entre o tempo inicial, o tempo final e a duração é: $$ d = t_F - t_I $$

Os tweens são usados para fazer animações com modelos parametrizados.

Tipos de Tweens

Os tweens descritos acima são lineares: a variação do parâmetro é proporcional ao tempo decorrido.

function draw(c, m) {
  c.fillStyle = "steelblue";
  c.fillRect(0, 0, 480, 120);
  c.fillStyle = "crimson";
  c.fillRect(m.linear.x, 10, 40, 40);
  c.fillStyle = "khaki";
  c.fillRect(m.nonlinear.x, 70, 40, 40);
}

const context = document
    .getElementById("anim:tween:1")
    .getContext("2d");

const model = {
  linear: {x:  10,},
  nonlinear: {x: 10}
};

const linear = new TWEEN.Tween(model.linear)
    .to({x: 430}, 2000)
    .easing(TWEEN.Easing.Linear.None)
    .yoyo(true)
    .repeat(Infinity)
    .start();

const cubic = new TWEEN.Tween(model.nonlinear)
    .to({x: 430}, 2000)
    .easing(TWEEN.Easing.Quadratic.InOut)
    .yoyo(true)
    .repeat(Infinity)
    .start();

const step = function(ctx, mdl) {
    TWEEN.update();
    draw(ctx, mdl);
    requestAnimationFrame(function () {
      step(ctx, mdl)
    });
  }

step(context, model);

Para animações com «objetos naturais» este tipo de tween não funciona bem porque produz movimentos uniformes, com velocidade constante.

• O resultado é semelhante ao movimento dos robots nos filmes antigos, ou de segunda categoria e também de alguns estilos de dança.

Os movimentos naturais não são lineares. Alguns aceleram no início e travam no fim. Outros têm uma fase de «ganhar balanço». As variantes são muitas.

• Easing define a aceleração de um tween e, em geral, tem as algumas variantes bem definidas.
• Ease-In tipo de aceleração no início da variação.
• Ease-Out tipo de aceleração no fim da variação.

Suporte para Tweens

A biblioteca tween.js proporciona um sistema flexível e eficiente para definir e usar tweens. Os tweens desta biblioteca:

1. São construídos com um valor inicial, um valor final e uma duração.
2. Aceitam uma grande variedade de easings.
3. Podem ser operados de várias formas:
   • yoyo: depois de atingir o valor final, o tween volta ao inicial.
   • repetir: o tween é repetido um certo número de vezes.
   • encadear: aplicar um segundo tween após a conclusão do primeiro.
   • etc.

O Ciclo de Animação

Qualquer animação é um ciclo infinito de atualização (update) e construção (render) de um modelo.

Os ciclos de animação e o uso dos tweens têm essencialmente a mesma estrutura e podem ser facilmente unificados.

Ciclo de Animação

const m = initial_model();
while (true) {
    m.update();
    m.render();
}

Ciclo dos Tweens

const t = TWEEN.Tween(...) ... ;
t.start();
while (true) {
    t.update();
    const x = t.value();
    ...
}

Programação Web e Ciclos Infinitos

Ciclos infinitos e requestAnimationFrame

No contexto da programação na Web, os ciclos infinitos devem ser implementados com a função requestAnimationFrame.

function draw(context, model) {
  /// Desenha o modelo atualizado no contexto fornecido.
}

function update(model) {
  // Por exemplo, usando TWEEN.update();
}

const model = {
  // valores iniciais dos parâmetros;
};

const step = function(ctx, mdl) {
    update(mdl);    // Atualiza os parâmetros do modelo.
    draw(ctx, mdl); // Desenha o modelo atualizado.
    requestAnimationFrame(function () { // Repete o ciclo de animação.
      step(ctx, mdl)
    });
  }

step(context, model); // Inicia o ciclo de animação.

A razão para fazer o ciclo de animação com a função requestAnimationFrame é que, desta forma, o navegador pode pausar a execução do código JavaScript quando necessário.

Na versão seguinte versão alternativa, o ciclo de animação é implementado usando um ciclo while infinito que bloqueia o navegador e portanto, deve ser evitado.

function draw(context, model) {
  /// Desenha o modelo atualizado no contexto fornecido.
}

function update(model) {
  // Por exemplo, usando TWEEN.update();
}

const model = {
  // valores iniciais dos parâmetros;
};

// BAD BAD NOT GOOD
while (true) {  // ** O NAVEGADOR FICA BLOQUEADO AQUI **
  update(model);        // Atualiza os parâmetros do modelo.
  draw(context, model); // Desenha o modelo atualizado.
}

Animação por passos

Embora flexíveis, nos tweens todos os valores estão determinados antes da animação começar. Uma vez iniciado, o tween vai seguir um «percurso» fixo, previsível.

Quando a animação dum objeto depende doutros objetos ou eventos, é necessário ir além dos tweens.

Por exemplo:

• Com movimentos baseados na física é preciso tratar da aceleração, colisões com outros objetos, etc.
• Os comportamentos reativos («seguir …», «olhar para …», etc) dependem dos valores de outros objetos.
• Os objetos controlados por interação (do teclado, rato, etc) dependem de valores externos ao próprio modelo.

m = initial_model();  // Inicialização do modelo
while (true) {        // Ciclo de animação
    m.update()          // Atualizar o modelo
    render(m)          // Construir a imagem
}

A estrutura básica da animação por tempo, com modelos parametrizados e o ciclo seguinte é válida em geral: a animação resulta da variação dos parâmetros calculada na atualização, quer esta variação resulte de tweens ou de outros cálculos.

Atualização Dinâmica

Intervalo entre fotogramas consecutivos
A atualização dos parâmetros adaptar-se ao intervalo entre fotogramas consecutivos.

Quando o tempo decorrido entre dois fotogramas não é constante, a atualização dos parâmetros do modelo tem de adaptar-se a essa variação.

Os tweens fazem automaticamente esta adaptação: O «valor» do tween é atualizado «internamente».

Para animações gerais, é necessário proporcionar, ao ciclo de animação, informação sobre o tempo: A forma universal e prática para lidar com a variação do tempo no ciclo da animação consiste em passar informação temporal para guiar a atualização dos parâmetros do modelo.

Revisitar o Ciclo de Animação

A função requestAnimationFrame é o elemento fundamental das animações na web (veja a documentação completa em MDN).

window.requestAnimationFrame(callback)

• A função indicada como argumento (callback) é «chamada» cada vez que o sistema (por exemplo, o browser) está pronto para iniciar um novo passo da animação.
• Quando a função callback é «chamada» recebe um único argumento, timestamp que assinala esse preciso momento.

function render(element, model) {
  const count   = model.count;
  const time    = Math.round(model.time * 0.001);
  const elapsed = Math.round(model.elapsed);
  const fps     = Math.round(1000 * model.count / model.time);
  element.innerHTML = `<table>` +
    `<tr><td>Count</td><td>Time</td><td>Elapsed (dt)</td><td>FPS</td></tr>` +
      `<tr>` +
      `<td> ${count} </td>` +
      `<td> ${time}s </td>` +
      `<td> ${elapsed}ms </td>` +
      `<td> ${fps} </td>` +
      `</tr>` +
  `</table>`;
}

let element = document.getElementById("anim:steps:counter");
let model = {
    count: 0, time: 0, elapsed: 0
};

let start_time = performance.now();
let last_time = performance.now();

animation_step = function (timestamp) {
    let progress = timestamp - start_time;
    let elapsed = timestamp - last_time;
    last_time = timestamp;
    model.count += 1;
    model.time = progress;
    model.elapsed = elapsed;
    render(element, model);
    requestAnimationFrame(animation_step);
}

requestAnimationFrame(animation_step);

Exemplo: Movimentos Baseados na Física

Para ilustrar uma aplicação da animação por passos usamos uma (simples) simulação física do movimento uniformemente acelerado.

Esta animação não é possível usando apenas tweens porque as colições e as interações modificam o modelo de formas que não podem ser antecipadas.

const model = {
  x: 64, y: 64,           //  ball position
  vx: 0, vy: 0,           //  ball velocity
  ax: 0, ay: 0,           //  ball acceleration
  r: 16,                  //  ball radius
  min_x: 0, max_x: 256,   //  box bounds: x
  min_y: 0, max_y: 256,   //  box bounds: y
  G: 0.25e-3, D: 0.8,     //  physics constants
  K: 0.8,                 //  kick strength
  kick: true,             //  kick flag
};

// Record time of the animation start
const start = performance.now();

// Record time of the previous step
let prev_ts = performance.now();

// Record time of the step start
const start_ts = performance.now();

// Animation step function
const step = function (ts) {
  const dt = ts - prev_ts;
  prev_ts = ts;

  // update acceleration
  if (model.kick) {   // KICK
    model.ax = model.K * linmap(model.x, model.min_x, model.max_x, -1, 1);
    model.ay = model.K * linmap(model.y, model.min_y, model.max_y, -1, 1);
    model.kick = false;
  } else {                // NO KICK
    model.ax = 0.0;
    model.ay = model.G; // gravity
  }

  // update velocity
  model.vx = model.vx + model.ax * dt;
  model.vy = model.vy + model.ay * dt;

  // update position
  model.x = model.x + model.vx * dt;
  model.y = model.y + model.vy * dt;

  // check collisions
  if (model.x - model.r < model.min_x) {
    model.vx = -model.D * model.vx;
    model.x = model.min_x + model.r;
  }
  if (model.x + model.r > model.max_x) {
    model.vx = -model.D * model.vx;
    model.x = model.max_x - model.r;
  }
  if (model.y - model.r < model.min_y) {
    model.vy = -model.D * model.vy;
    model.y = model.min_y + model.r;
  }
  if (model.y + model.r > model.max_y) {
    model.vy = -model.D * model.vy;
    model.y = model.max_y - model.r;
  }

  // Render the model in the graphics system
  render(context, model);
  requestAnimationFrame(step);
}
requestAnimationFrame(step);

Exercícios

Desenho original por Enki Bilal

Exercícios Javascript

Funções geradoras

Funções que geram coleções de valores.

Uma coleção é uma estrutura de dados que armazena ou produz valores, como arrays ou listas.

Por exemplo:

const numbers = [1, 2, 3, 4];

1. Escreva uma função repete(x, n) que devolve um array com n cópias de x.
2. Escreva uma função aleatorios(n) que devolve um array com n números aleatórios.
3. Escreva uma função intervalo(a, b) que devolve um array com os números inteiros entre a e b incluindo ambos os extremos. Se b < a o resultado deve ser a lista vazia [].
4. Escreva uma função linspace(a, b, n) que enche um array com n números reais (float) entre a e b, igualmente espaçados.
   • Por exemplo linspace(0, 1, 3) devolve [0.0, 0.5, 1.0].

Filtros

Funções que selecionam elementos de uma coleção.

Em geral, a seleção pode ser feita por meio de condições booleanas.

Por exemplo:

const even_numbers = numbers.filter(x => x % 2 === 0);
// [2, 4]

1. Escreva uma função pares(x) que tem como argumento um array x de números inteiros e que devolve um array apenas com os números pares.
   • Por exemplo pares([1, 2, 4, 5, 2, 3]) devolve [2, 4, 2].
2. Escreva uma função positivos(x) que tem como argumento um array x de números reais e que devolve um array apenas com os números positivos.
   • Por exemplo positivos([1, -2.5, 0.4, 0.0, -1.5, 2, 2.3]) devolve [1, 0.4, 2, 2.3].
3. Escreva uma função limite_sup(x, a) que tem como argumentos um array x de números reais e um valor a e que devolve um array apenas com os números menores ou iguais que o valor a.
   • Por exemplo limite_sup([1, -2.5, 0.4, 0.0, -1.5, 2, 2.3], 0.4) devolve [-2.5, 0.4, 0.0, -1.5].
4. Escreva uma função filtro(f, x) que tem como argumentos uma função f: float -> boolean e um array x de números reais e que devolve um array apenas com os números xi de x tais que f(xi) === true.
   • Por exemplo filtro(x => x % 2 === 0, [1, 2, 4, 5, 2, 3]) devolve [2, 4, 2]. Quais das alíneas acima consegue tornar a resolver usando esta função?

Mapas

Funções que transformam elementos de uma coleção.

Em geral, a transformação pode ser feita por uma função que aplica um valor num outro valor.

Por exemplo:

const square_numbers = numbers.map(x => x ** 2);
// [1, 4, 8, 16]

1. Escreva uma função dobro(x) que tem como argumento um array x de números reais e que devolve um array com os dobros desses números.
   • Por exemplo dobro([1, 2.1, 4, 5, -2, 3]) devolve [2, 4.2, 8, 10, -4, 6].
2. Escreva uma função quadrado(x) que tem como argumento um array x de números reais e que devolve um array com os quadrados desses números.
   • Por exemplo quadrado([1, -2.5, 0.4]) devolve [1, 6.25, 0.16].
3. Escreva uma função unicos(x) que tem como argumento um array x de números reais e que devolve um array sem valores repetidos.
   • Por exemplo unicos([1, -2.5, 1]) devolve [1, -2.5].
4. Escreva uma função crescente(x) que tem como argumento um array x de números reais e que devolve um array com os valores por ordem crescente.
   • Por exemplo crescente([1, -2.5, 1]) devolve [-2.5, 1, 1].
5. Escreva uma função estender(x, n) que tem como argumento um array x de números reais e um valor inteiro n e que devolve um array exatamente de comprimento n. Se o comprimento de x for menor que n devem ser acrescentados zeros suficientes. Se o comprimento de x for maior que n os valores a mais são descartados.
   • Por exemplo estender([1, -2.5], 4) devolve [1, -2.5, 0, 0], e estender([1, 6.25, 0.16], 2) devolve [1, 6.25].
6. Escreva uma função mapa(f, x) que tem como argumentos uma função f: float -> float e um array x de números reais e que devolve um array com números yi = f(xi) em que x = [ ..., xi, ...].
   • Por exemplo mapa(x => 2 * x, [1, 2.1, 4, 5, -2, 3]) devolve [2, 4.2, 8, 10, -4, 6]. Quais das alíneas acima consegue tornar a resolver usando esta função?

Combinações

Funções que combinam uma ou várias coleções numa coleção nova.

Por exemplo:

const descending_numbers = numbers.reverse();
// [4, 3, 2, 1]
const seesaw = numbers.concat(descending_numbers);
// [1, 2, 3, 4, 4, 3, 2, 1]

1. Escreva uma função inverte(x) que tem como argumentos o array x de números reais e que devolve um array com os valores de x por ordem inversa (do último para o primeiro).

2. Assegure-se que x = cadeia(cabeca(n, x), cauda(n, x)) para qualquer x e qualquer n, em que:

   1. A função cadeia(x, y) tem como argumentos dois array x, y de números reais e devolve um array com os valores de x seguidos pelos valores de y.
      • Por exemplo cadeia([1, 2.1, 4], [5, -2, 3]) devolve [1, 2.1, 4, 5, -2, 3].
   2. A função cabeca(n, x) tem como argumentos o int n e o array x de números reais e devolve o array dos primeiros n valores de x.
   3. A função cauda(n, x) tem como argumentos o int n e o array x de números reais e devolve o array com os valores de x a partir do n-ésimo elemento.

3. Escreva uma função somar(x, y) que tem como argumentos dois array x, y de números reais e que devolve um array com os valores de x somados aos valores de y pela mesma ordem. Se os argumentos tiverem comprimentos diferentes o resultado deve ser a lista vazia: [].

   • Por exemplo somar([1, 2.1, 4], [5, -2, 3]) devolve [6, 0.1, 7] e somar([1, 2], [3]) devolve [].

4. Escreva uma função emparelhar(x, y) que tem como argumentos dois array x, y de números reais e que devolve um array com objetos {x: xi, y: yi} onde xi, yi estão nas mesmas posições de x, y. Se os argumentos tiverem comprimentos diferentes o resultado deve ser a lista vazia: [].

   • Por exemplo emparelhar([1, 2.1, 4], [5, -2, 3]) devolve [{x: 1, y: 5}, {x: 2.1, y: -2}, {x: 4, y: 3}] e emparelhar([1, 2], [3]) devolve []. Consegue usar a função mapa do exercício anterior para resolver esta alínea?

Reduções

Funções que reduzem uma coleção a um valor.

Por exemplo:

const numbers_count = numbers.length;
// 4
Math.min(...numbers);
// 1

1. Escreva uma função conta(x) que tem como argumento um array x de números reais e que devolve o comprimento do array.
   • Por exemplo conta([1, 2, 3, 4]) devolve 4.
2. Escreva uma função soma(x) que tem como argumento um array x de números reais e que devolve a soma desses números.
   • Por exemplo soma([1, 2, 3, 4]) devolve 10.
3. Escreva uma função media(x) que tem como argumento um array x de números reais e que devolve a média desses números.
   • Por exemplo media([1, 2, 3, 4]) devolve 2.5.
4. Escreva uma função max(x) que tem como argumento um array x de números reais e que devolve o maior desses números.
   • Por exemplo max([1, 2, 3, 4]) devolve 4.
5. Escreva uma função min(x) que tem como argumento um array x de números reais e que devolve o menor desses números.
   • Por exemplo min([1, 2, 3, 4]) devolve 1.
6. Escreva uma função stats(x) que tem como argumento um array x de números reais e que devolve um sumário estatístico desses valores: um objeto com atributos count, mean, stdev, min, max. O atributo count é o comprimento de x, os valores de mean, min, max resultam das alíneas anteriores e stdev (o desvio padrão) pode ser calculado pela fórmula $$\textrm{stdev}(x) = \sqrt{\frac{1}{n - 1}\sum (x_i - m)^2}$$ onde $n$ é a dimensão do vetor e $m$ a sua média.
   • Por exemplo stats([1, 2, 3, 4]) devolve {count: 4, mean: 2.5, stdev: 1.291, min: 1, max: 4}.

Álgebra Linear

Métodos numéricos fundamentais para a computação gráfica.

Por exemplo:

Um segmento pode ser definida por dois pontos, $A = (a_x, a_y)$ e $B = (b_x, b_y)$. O comprimento deste segmento resulta do produto interno através da fórmula

$$ \overline{AB} = \lVert B - A \rVert = \sqrt{(B - A) \cdot (B - A)}= \sqrt{(b_x - a_x)^2 + (b_y - a_y)^2} $$

1. Escreva uma função dot(x, y) que tem como argumentos dois array x, y de números reais e que devolve o produto interno dos vetores $x$ e $y$. O produto interno de $x = (x_1,\ldots, x_n)$ e $y = (y_1,\ldots, y_n)$ é $$ x \cdot y = \sum x_i y_i $$ Se os argumentos tiverem comprimentos diferentes o resultado deve ser a lista vazia: [].
   • Por exemplo dot([1, 2, 3], [4, 5, 6]) devolve 32. Torne a resolver esta alínea usando as alíneas e exercícios anteriores.
2. Escreva uma função norma(x) que tem como argumento um array x de números reais e que devolve a norma do vetor $x$.
   • Por exemplo norma([1, 1]) devolve 1.4142135624. Lembre-se que a norma de um vetor $x = (x_1,\ldots, x_n)$ é $$\lVert x \rVert = \sqrt{\sum x_i^2} = \sqrt{x \cdot x}. $$

Exercícios 2D

Reveja a matéria de Álgebra Linear e de Geometria Analítica.

Geometria 2D

Distância de um ponto a uma reta

1. A distância ($\color{seagreen}{d}$) entre o ponto vermelho ($\color{crimson}{A}$) e a reta azul é a distância entre o ponto vermelho ($\color{crimson}{A}$) e o ponto azul ($\color{steelblue}{B}$).
2. O ponto azul ($\color{steelblue}{B}$) é a interseção entre a reta azul e a reta verde tracejada.
3. A reta verde tracejada tem equação paramétrica $\color{seagreen}{X = A + \lambda u}$; falta determinar o vetor $u$.
4. O vetor $u$ da reta verde tracejada é perpendicular ao vetor $v$ da equação paramétrica reta azul ($\color{steelblue}{X = B + \lambda v}$): $$u = (u_x, u_y) = (-v_y, v_x)$$

Exercício 1

Considere a equação paramétrica da reta, $X = P + \lambda v$.

Suponha que são dados dois pontos, $A = (a_x, a_y)$ e $B=(b_x, b_y)$.

Determine os valores dos parâmetros $P, v$ da reta que passa em $A, B$ e tais que:

• $A = P + \lambda v$ quando $\lambda = 0$ e
• $B = P + \lambda v$ quando $\lambda = 1$.

Exercício 2

Escreva uma expressão matemática para definir:

1. Os segmentos de reta $(0,0) - (0,1)$, $(0,0) - (1,0)$ e $(0,0) - (1,1)$.
2. O triângulo de vértices $(0,0) - (0,1) - (1,0)$.
3. O quadrado $(0,0) - (1,0) - (1,1) - (0,1)$.
4. O interior do quadrado e triângulo anteriores.

Exercício 3

Encontre os valores dos parâmetros da equação paramétrica:

1. Da reta:
   1. Que passa nos pontos $(0,0)$ e $(0,1)$.
   2. Que passa nos pontos $(0,0)$ e $(1,0)$.
   3. Que passa nos pontos $(0,0)$ e $(1,1)$.
2. Da reta com equação algébrica:
   1. $2x + 3y - 4 = 0$.
   2. $3x - 2y - 4 = 0$.
   3. $4x + 6y - 8 = 0$.
3. Da circunferência:
   1. Centrada em $(0,1)$ e de raio $2$.
   2. Centrada em $(1,0)$ e de raio $2$.
   3. Centrada em $(1,1)$ e de raio $2$.
   4. Centrada em $(0,1)$ e que passa no ponto $(0,0)$.
   5. Centrada em $(1,0)$ e que passa no ponto $(0,0)$.
   6. Centrada em $(1,1)$ e que passa no ponto $(0,0)$.

Programação 2D

Reveja a programação, em particular a linguagem JavaScript.

Exercício 4

Calcule os parâmetros $A, B, C$ da equação algébrica da reta ($Ax + By + C = 0$), dadas as coordenadas $(x_1, y_1), (x_2, y_2)$ de dois pontos.

1. Implemente a função eqna_s(x1, y1, x2, y2) que devolve um objeto com atributos {A, B, C}.
2. Em que casos é que as entradas x1, y1, x2, y2 não definem uma reta? No seu código detete esse caso e devolva null.
3. Em que casos é que $A_1, B_1, C_1$ define a mesma reta que $A_2, B_2, C_2$? Implemente uma função equala_ss(A1, B1, C1, A2, B2, C2) que devolve true se os parâmetros definem a mesma reta e false caso contrário.

Exercício 5

Calcule os parâmetros $P, v$ da equação paramétrica da reta ($X = P + \lambda v$), dadas as coordenadas $(x_1, y_1), (x_2, y_2)$ de dois pontos.

1. Implemente a função eqnp_s(x1, y1, x2, y2) que devolve um objeto com atributos {P, v}.
2. Em que casos é que as entradas x1, y1, x2, y2 não definem uma reta? No seu código detete esse caso e devolva null.
3. Em que casos é que os parâmetros $P_1, v_1$ definem a mesma reta que os parâmetros $P_2, v_2$? Implemente uma função equalp_ss(P1, v1, P2, v2) que devolve true se os parâmetros definem a mesma reta e false caso contrário.

Exercício 6

Implemente uma função dot(x1, y1, x2, y2) para calcular o produto interno $$(x_1, y_1) \cdot (x_2, y_2) = x_1 x_2 + y_1 y_2$$

Use essa função para implementar funções para calcular:

1. O comprimento de um vetor, length_v: $|v| = \sqrt{v\cdot v}$.
2. A distância entre dois pontos, dist_pp: $d(A,B) = | B - A |$.
3. A distância de um ponto a uma reta, dist_ps. Sugestão: Use a equação paramétrica da reta.
4. O «reflexo» de um ponto por uma reta, mirror_ps.
5. O «reflexo» de uma reta por outra reta, mirror_ss.
6. Se duas retas são perpendiculares, are_perp.

Exercício 7

Pode gerar pontos de uma circunferência usando uma equação paramétrica.

Implemente a função points_c(x1, y1, r, n) que gera uma lista com $n$ pontos equidistantes da circunferência de centro $(x_1, y_1)$ e raio $r$.

Use a função points_c para estimar a distância de uma circunferência a:

1. Um ponto: edist_cp.
2. Uma reta: edist_cl.
3. Outra circunferência: edist_cc.

Exercício 8

Pode gerar pontos de um segmento de reta usando os dois extremos do segmento e uma equação paramétrica.

Implemente a função points_s(x1, y1, x2, y2, n) que gera uma lista com $n$ pontos equidistantes do segmento limitado pelos pontos $(x_1, y_1)$ e $(x_2, y_2)$. Sugestão: Use a equação vetorial da reta: $$ (x,y) = (x_1, y_1) + \lambda ( x_2 - x_1, y_2 - y_1 ) $$

Estime a distância de um segmento de reta a:

1. Um ponto: edist_sp.
2. Outro segmento de reta: edist_ss.
3. Uma circunferência: edist_sc. Suponha que esta circunferência:
   1. Está definida por centro e raio.
   2. Está aproximada por um conjunto de pontos.

Exercício 9

A forma de representar as coordenadas dos pontos usada acima é muito «trapalhona».

Em vez de usar x1, y1 (ou outros indíces) use listas, P1 = [x1, y1], para representar pontos. Atualize todas as funções anteriores.

Por exemplo, x = dot(P, Q).

Exercício 10

Pode obter formas simples usando apenas conjuntos de pontos para definir o contorno do objeto gráfico.

Implemente:

1. A função join(A, B) em que A e B são listas de pontos e que devolve a lista que resulta de acrescentar os pontos de B a seguir aos pontos de A.

2. A função frame(A) que calcula os cantos superior esquerdo e inferior direito dos pontos em A, isto é, a moldura para os pontos de A.

3. A função min_circ(A) que calcula a menor circunferência que contém todos os pontos de A. Resolva em duas versões: uma que devolve o centro e o raio da circunferência e outra que devolve uma aproximação com $n$ pontos.

Exercício 11

Pode transformar pontos usando as operações da álgebra linear.

Implemente a função [x1, y1, z1] = dot_mv(a,b,c,d,e,f,g,h,i,x0,y0,z0) que calcula $$\begin{bmatrix} x_1 \cr y_1 \cr z_1 \end{bmatrix} = \begin{bmatrix} a & b & c \cr d & e & f \cr g & h & i \end{bmatrix} \begin{bmatrix} x_0 \cr y_0 \cr z_0 \end{bmatrix}. $$

Esta forma de representar matrizes e vetores é muito «trapalhona».

Represente os vetores por listas, v = [x, y, z], e as matrizes por listas de listas, A = [[a, b, c], [d, e, f], [g, h, i]]. Note que A[0] é a primeira linha de A.

Deve ficar com uma função X1 = dot_mv(A, X0).

Exercício 12

Implemente funções para gerar matrizes e calcular operações comuns.

1. A matriz zeros(n,m) tem $n$ linhas, $m$ colunas e todas as entradas são $0$.
2. Na matriz ones(n, m) tem $n$ linhas, $m$ colunas e todas as entradas são $1$.
3. A matriz eye(n) é a matriz identidade de ordem $n$.
4. A função t(A) é a matriz transposta de $A$.
5. A função sum_mm(A, B) soma as matrizes $A$ e $B$. Se as dimensões forem incompatíveis, devolve null.
6. A função dot_mm(A, B) multiplica as matrizes $A$ e $B$. Se as dimensões forem incompatíveis, devolve null.
7. A função translate(dx, dy) devolve a matriz da translação por $(dx, dy)$.
8. A função rotate(alpha) devolve a matriz da rotação por $\alpha$ radianos.
9. A função scale(sx, sy) devolve a matriz da escala por $(sx, sy)$.

Exercício 13

Use a biblioteca de funções que definiu acima para construir e transformar (aproximações) de circunferências e de segmentos.

Visualize as formas originais (a verde) e transformadas (a vermelho) nos sistemas C2D e SVG.

Exercício 14

Implemente a regra par-ímpar de enchimento de formas.

Suponha que F é um conjunto de pontos que aproxima uma figura 2D:

1. Defina a função sort_h(F) que devolve os pontos de F ordenados da esquerda para a direita (isto é, primeiro os pontos com menor coordenada x).
2. Defina a função strip_h(F, y0, e) que devolve os pontos de F que estão numa faixa horizontal, isto é os pontos de F cuja coordenada $y$ é tal que $\left| y - y_0 \right| \leq e$. Se não existirem pontos assim em F, devolve a lista vazia.
3. Defina a função first_left(F) que devolve o ponto mais à esquerda de F. Se F for uma lista vazia devolve null.
4. Defina a função next_right(F, x0) que devolve o ponto de F que, de todos os pontos de F com coordenada x maior que x0, é o que tem menor coordenada x. Se não existir tal ponto devolve null.
5. Use as funções sort_h, strip_h, first_left e next_right para definir a função fill_evenodd(F, ...​), que implementa a regra par-ímpar por faixas horizontais.
   • O resultado deve ser uma lista com os segmentos horizontais interiores, sendo cada segmento definido por dois pontos.
   • Considere ainda que argumentos são úteis e/ou necessário e como detetar e assinalar potenciais erros.

Exercício 15

Visualize o preenchimento de formas pela regra par-ímpar.

Use vermelho para a forma e verde para o interior. Resolva esta alínea para os sistemas C2D e SVG.

Exercício 16

Visualize o interior da forma usando os sistemas C2D e SVG com:

1. Um gradiente horizontal com várias cores (pelo menos 3).
2. Um gradiente vertical com várias cores (pelo menos 3).
3. Um padrão xadrez.

Modelação 2D

Exercício 17

Escreva um programa que use o C2D para desenhar um caminho entre os pontos de coordenadas $(0,0)$ e $(64,64)$ que tenha um arco de raio 16.

Exercício 18

Escreva um programa javascript para o C2D que desenhe um círculo amarelo no meio de um retângulo 100x100 azul. Defina a mesma imagem com um documento SVG.

Exercício 19

Procure na internet: Qual é o intervalo dos comprimentos de onda das cores visíveis?

Exercício 20

Marque os seguintes pontos num referencial cartesiano e num referencial de ecrã (desenhados numa folha de papel): (1, 3), (-2, 1.5), (0, -2), (0, 0), (2, 1), (-1.5, 1.5), (3, -0.5).

Exercício 21

Meia Lua	Yin-Yang

Escreva um programa para o C2D, e um documento SVG para desenhar:

1. Uma meia lua (ver acima).
2. Um quadrado centrado e rodado 45º.
3. Um tabuleiro de xadrez.
4. Um tabuleiro tri-colorido. Generalize para uma função que desenhe um tabuleiro $n$-colorido.
5. → O símbolo oriental Yin-Yang (ver acima).
6. Um retângulo pintado com um gradiente radial acíclico.
7. Um retângulo pintado \com um gradiente radial cíclico.
8. → Um octógono. Generalize para um $n$-ágono.
9. → Uma estrela de cinco pontas. Generalize para $n$ pontas.
10. Desenhe a bandeira da união europeia.

Exercício 23

Implemente uma função grafico(f, n, a, b) para ajudar a desenhar o gráfico de uma função matemática.

• Esta função devolve $n$ pontos $(x_i, f(x_i))$ do gráfico da função $f: \mathbb{R} \to \mathbb{R}$, com as abcissas $x_i$ igualmente espaçadas entre $a$ e $b$ (e $x_0 = a, x_{n-1} = b$).
• Implemente funções para adaptar as listas $[(x_0, f(x_0)), \ldots, (x_{n-1}, f(x_{n-1}))]$ a caminhos C2D e SVG.

Exercício 24

Implemente uma pequena biblioteca gráfica 2D.

Suponha que cada objeto gráfico é definido por:

• Um caminho, isto é uma lista de pontos x, y.
• Uma transformação com uma translação, uma rotação e uma escala.
• Propriedades de aspeto (stroke e fill).

Implemente uma função para desenhar estes objetos gráficos num C2D e para produzir um elemento SVG.

Exercícios 3D

Reveja a matéria de Álgebra Linear e de Geometria Analítica.

Geometria 3D

Exercício 1

Vetor Perpendicular 1

1. Dados dois vetores 3D $u = (u_x, u_y, u_z)$ e $v = (v_x, v_y, v_z)$, como é que encontra um terceiro vetor $w=(w_x, w_y, w_z)$ perpendicular a ambos?
2. Como é que adapta a resolução da alínea anterior para o caso em que, em vez de dois vetores, são dados três pontos 3D, $A=(A_x, A_y, A_z), B=(B_x, B_y, B_z)$ e $C=(C_x, C_y, C_z)$?

Exercício 2

Posições, direções e alvos

No sistema 3JS a iluminação SpotLight é definida por uma posição $p = (p_x, p_y, p_z)$ e um alvo $t = (t_z, t_y, t_z)$, de forma que o foco de luz fica posicionado em $p$ e aponta para $t$.

Já no sistema X3D o mesmo tipo de iluminação é definido por uma posição $p$ análoga à de cima mas, em vez dum alvo, usa uma direção $d = (d_x, d_y, d_z)$, de forma que o foco de luz fica posicionado em $p$ a aponta na direção $d$.

1. Como obtém $d$ em função de $p$ e $t$ de forma que um raio emitido a partir da posição $p$ apontado ao alvo $t$ tem a direção $d$??
2. Como obtém $t$ em função de $p$ e $d$ de forma que um raio emitido a partir da posição $p$ na direção $d$ atinge um alvo em $t$.

Programação 3D

Representação de Coordenadas. Nestes exercícios pontos e vetores 3D são representados por objetos {x, y, z} de forma que o valor de cada atributo indica a respetiva cooredenada. Pontos e vetores 2D ficam representados por objetos {x, y} (ou {u, v} no caso de texturas).

Exercício 3

Operações 3D

1. Implemente a função sum(u, v) que calcula a soma de dois vetores u e v: $$ \mathrm{sum}(u, v) = u + v = (u_x + v_x, u_y + v_y, u_z + v_z) $$
2. Implemente a função scalar(a, u) que calcula o produto do escalar a pelo vetor u e use-a para definir minus(u) que calcula o simétrico do vetor u: $$ \begin{aligned} \mathrm{scalar}(a, u) &= au &&= (a \times u_x, a \times u_y, a \times u_z) \cr \mathrm{minus}(u) &= -u &&= \mathrm{scalar}(-1, u) \end{aligned} $$
3. Implemente a função inner(u, v) que calcula o produto interno de dois vetores u e v: $$ \mathrm{inner}(u, v) = u\cdot v = u_x \times v_x + u_y \times v_y + u_z \times v_z $$
4. Implemente a função norm(u) que calcula a norma do vetor u: $$ \mathrm{norm}(u) = \left| u \right| = \sqrt{u \cdot u } = \mathrm{sqrt}(\mathrm{inner}(u, u)) $$
5. Implemente a função dist(p, q) que calcula a distância entre dois pontos p e q: $$ \mathrm{dist}(p, q) = \left| p - q \right| = \mathrm{norm}( \mathrm{sum}(p, \mathrm{minus}(q)) ) $$
6. Implemente a função vers(u) que calcula o versor do vetor u; o versor de $u$ é um vector $v$ com norma $\left| v \right| = 1$ e com a mesma direção de $u$: $$ \mathrm{vers}(u) = \frac{1}{\left| u \right|} u = \mathrm{scalar}\left( \frac{1}{\mathrm{norm}(u)}, u\right) $$
7. A fórmula $$u\cdot v = \left|u\right|\left|v\right|\cos\alpha$$ permite obter $\alpha$, o ângulo entre $u$ e $v$. Implemente a função angle(u, v)que calcula o ângulo entre dois vetores u e v: $$ \mathrm{angle}(u, v) = \arccos\left( \frac{u \cdot v}{ \left| u \right| \left| v \right|} \right) = \arccos\left( \frac{\mathrm{inner}(u, v)}{ \mathrm{norm}(u)\mathrm{norm}(v)} \right) $$
8. Implemente a função are_colin(u, v) que devolve o booleano true se u e v forem co-lineares e false caso contrário. Os vetores $u$ e $v$ são co-lineares de existe um escalar $\lambda \not= 0$ tal que $v = \lambda u$: $$ \mathrm{are_colin}(u, v) = \mathrm{angle}(u, v) == 0 $$

Exercício 4

Produto Externo

Supondo que $w = u \otimes v$ é o produto externo de $u$ e $v$, então as componentes de $w$ podem ser calculadas por $$ w_x \mathbf{x} + w_y \mathbf{y} + w_z \mathbf{z} = \begin{vmatrix} \mathbf{x} & \mathbf{y} & \mathbf{z} \cr u_x & u_y & u_z \cr v_x & v_y & v_z \end{vmatrix} $$

1. Implemente a função outer(u, v) que calcula o produto externo entre dois vetores dados.
2. Implemente a função perp(u, v) que calcula um vetor perpendicular a dois vetores dados.
3. Implemente a função basis(u, v) que calcula uma base a partir de u e v:
   1. A função levanta uma exceção se u e v forem co-lineares.
   2. Caso contrário devolve uma lista de três vetores [a, b, c] em que
      • a é o versor de u,
      • b é o versor de v,
      • c é um vetor de norma $1$ perpendicular a u e a v.

Exercício 5

Conjuntos de Pontos

1. Centro. Implemente a função center(points) que calcula o centro de um array de pontos.
2. Próximo. Implemente a função nearest(target, points) em que target é um ponto 3D e points é um array de pontos 3D e que encontra o elemento de points que está mais próximo de target.
   • A sua função deve devolver um objeto com atributos {d, p} em que d é a distância e p o ponto mais próximo.
3. Afastado. Implemente a função farthest(target, points) em que target é um ponto 3D e points é um array de pontos 3D e que encontra o elemento de points que está mais afastado de target. Resolva de forma semelhante à alínea anterior.
4. «Mais Isolado». Implemente a função loneliest(points) em que points é um array de pontos 3D e que encontra o ponto «mais isolado» de um conjunto de pontos. O ponto «mais isolado» é o que está mais distante do centro.
5. «Mais Central». Implemente a função centralest(points) em que points é um array de pontos 3D e que encontra o ponto «mais central» de um conjunto de pontos. O ponto «mais central» é o que está mais perto do centro.
6. Canto Superior Direito Anterior. Implemente a função corner_trf(points) (trf: top right front) em que points é um array de pontos 3D e que encontra o «canto superior direito anterior» (SDA) de um conjunto de pontos. As coordenadas do SDA são os valores máximos nos eixos $x$, $y$ e $z$. Por exemplo:

   let points =  [
       {x: -1, y: 2, z: 0},
       {x: 20, y: 1, z: 3}
   ];
   
   {x: 20, y: 2, z: 3} === corner_tlf(points);
   

7. Canto Inferior Esquerdo Posterior. Implemente a função corner_llb(points) (lrb: lower left back) nos mesmos moldes do exercício anterior, substituindo o máximo pelo mínimo.
8. Pontos Mais Afastados. Implemente a função most_apart(points) em que points é um array de pontos 3D e que encontra os dois elementos de points que estão mais afastados um do outro. Isto é, se $p, q$ forem esses pontos então, dados quaisquer dois pontos $a$ e $b$ em points então dist(a,b) <= dist(p,q).
9. Pontos Menos Afastados. Implemente a função least_apart(points) em que points é um array de pontos 3D e que encontra os dois elementos distintos de points que estão menos afastados um do outro. Isto é, se $p, q$ forem esses pontos então, dados quaisquer dois pontos $a$ e $b$ em points então dist(a,b) >= dist(p,q).

Exercício 6

Processamento de Extrusões

Na construção de uma extrusão a secção percorre a espinha. Suponha que:

• A secção é definida por um array de pontos 2D {x, z} (note que é usado z e não y).
• A espinha é definida por um array de vetores 3D {x, y, z}.

Estes dois parâmetros definem os vértices da geometria obtida por extrusão.

Mais concretamente, cada ponto p:{x, z} da secção e cada vetor v:{x, y, z} da espinha definem o vértice q = {x: p.x + v.x, y: v.y, z: p.z + v.z} da extrusão.

Por exemplo, dados

const section = [
    {x: 0.0, z: 0.0},
    {x: 1.0, z: 0.0},
    {x: 0.0, z: 1.0} ];

const spine = [
    {x: 0.0, y: 0.0, z: 0.0},
    {x: 0.0, y: 1.0, z: 0.0},
    {x: 1.0, y: 2.0, z: -1.0} ];

o ponto

section[2] === {x: 0.0, z: 1.0}

e o vetor

spine[1] === {x: 0.0, y: 1.0, z: 0.0}

definem o vértice

{x: 0.0, y: 1.0, z: 1.0}

Escreva a função vertex(i, j, section, spine) que devolve as coordenadas xyz do vértice definido pelo i-ésimo ponto da secção e pelo j-ésimo passo da espinha.

• Por exemplo, usando as variáveis acima, vertex(1, 2, section, spine) é o ponto 3D {x: 2.0, y: 2.0, z: -1.0}, que resulta do ponto {x: 1.0, z: 0.0} (com índice i = 1) e do vetor {x: 1.0, y: 2.0, z: -1.0} (com índice j = 2).
• Assegure-se que i e j são índices válidos. Se não, a função deve devolver null.

Exercício 7

Posições, direções e alvos (em JavaScript)

No sistema 3JS a iluminação SpotLight é definida por uma posição $p = (p_x, p_y, p_z)$ e um alvo $t = (t_z, t_y, t_z)$, de forma que o foco de luz fica posicionado em $p$ e aponta para $t$.

Já no sistema X3D o mesmo tipo de iluminação é definido por uma posição $p$ análoga à de cima mas, em vez dum alvo, usa uma direção $d = (d_x, d_y, d_y)$, de forma que o foco de luz fica posicionado em $p$ a aponta na direção $d$.

Escreva funções JavaScript de acordo com as seguintes especificações:

1. Pontos e vetores são representados por objetos {x, y, z} de forma que o valor de cada atributo indica a respetiva cooredenada.
2. A função direction(p, t) devolve um vetor d de forma que um raio emitido a partir da posição p apontado ao alvo t tem a direção d = direction(p, t).
3. A função target(p, d) devolve uma posição t de forma que um raio emitido a partir da posição p na direção d atinge um alvo em t = target(p, d).

Modelação 3D

Resolva cada um destes exercícios usando as duas bibliotecas gráficas para 3D, X3D e 3JS.

Exercício 8

Modelar um referencial.

Modele um referencial XYZ. Assegure-se que os eixos estão corretamente orientados e use o seguinte esquema de cores: X:red; Y:green; Z:blue.

Exercício 9

Modelar uma pirâmide.

Modele uma pirâmide usando uma geometria por faces.

Exercício 10

Modelar um frustum.

Um frustum (veja também o artigo na wikipédia) é um poliedro (isto é, um sólido com todas as faces planas) com duas das faces quadradas paralelas (o topo e a base).

Modele um frustum, usando uma geometria por faces, com altura 1, em que a base é um quadrado de lado 2 e o topo um quadrado de lado 1.

Exercício 11

Modelar um octaedro.

Octaedro

Um octaedro é um dos cinco sólido platónicos (veja o artigo na wikipédia); tem oito faces triangulares e seis vértices:

$$ (0,1.5,0), (-1,0,1), (1,0,1), (1,0,-1), (-1,0,-1), (0,-1.5,0) $$

Modele um octaedro usando uma geometria por faces.

Exercício 12

Modelar um icosaedro.

Icosaedro

Um icosaedro é um dos cinco sólido platónicos (veja o ) e tem os vértices seguintes:

$$ \begin{aligned} && (0,\phi,1) && (0,\phi,-1) \cr && (-\phi,1,0) && (\phi,1,0) \cr (1,0,\phi) && (1,0,-\phi) && (-1,0,-\phi) && (-1,0,\phi) \cr && (-\phi,-1,0) && (\phi,-1,0) \cr && (0,-\phi,-1) && (0,-\phi,1) \end{aligned} $$ onde $\phi = \frac{\sqrt{5} + 1}{2} \approx 1.62$.

Modele um icosaedro usando uma geometria por faces.

Exercício 13

Pintar uma pirâmide.

Modele uma pirâmide com as texturas de difusão, brilho e normais obtidas de imagens feitas ou encontradas por si. Seja realista.

Exercício 14

Pintar uma tenda.

Os vértices de uma tenda estão dados abaixo

$$ \begin{aligned} &(0.0, 1.5, 0.0)\cr\cr (-.7, 1.0, 0.7) && (0.7, 1.0, 0.7)\cr (0.7, 1.0, -.7) && (-.7, 1.0, -.7)\cr\cr (-1., 0.0, 1.0) && (1.0, 0.0, 1.0)\cr (1.0, 0.0, -1.) && (-1., 0.0, -1.) \end{aligned} $$

Modele uma tenda pintada com texturas feitas (ou encontradas) por si. Seja realista.

Exercício 15

Iluminar uma pirâmide e uma tenda.

Use os modelos da pirâmide e da tenda que construiu com texturas de difusão, reflexos e normais e ilumine-a com:

• Uma fonte “direcional”.
• Uma fonte “ponto”.
• Uma fonte “foco”.

No caso do sistema X3D desligue a iluminação “geral” colocando o seguinte elemento no nó <Scene>:

<NavigationInfo headLight="false"></NavigationInfo>

Exercícios Animação

Geometria 2D

Exercício 1 - Sistemas de Coordenadas

Sistemas de Coordenadas
Coordenadas Cartesianas $x$$y$ e Polares $d$$a$

Num referencial cartesiano cada ponto do plano (assinalado ●) é identificado por coordenadas cartesianas $x$ e $y$.

Esta não é a única forma de representar por números os pontos do plano. Outra forma —conveniente na animação do movimento— consiste em definir uma direção $a$ e uma distância $d$.

Considere um ponto no plano: $p = \textrm{cart}(x, y) = \textrm{polar}(d, a)$. Então:

$$ \begin{aligned} x &= d \cos{a} \cr y &= d \sin{a} \cr d &= \sqrt{x^2 + y^2} \cr a &= \arctan\left(- \frac{y}{x}\right) \end{aligned} $$

A última expressão tem alguns problemas de domínio pelo que, no JavaScript, existe uma função dedicada a esse cálculo, Math.atan2.

Implemente duas funções, pol2cart e cart2pol para passar de um referencial para o outro.

Tweens

Exceto quando indicado o contrário, cada exercício é para ser resolvido em SVG, C2D, X3D e 3JS.

Exercício 2 - Percursos

Percursos

1. Percursos Lineares Uniformes. Desenhe uma forma simples (por exemplo, uma bola ou uma esfera azul) e desloque-a:

   1. 200 pixeis para a direita.
   2. Num retângulo com 200 pixeis de largura e 100 de altura.
   3. Num caminho poligonal com n pontos.

2. Percursos Curvos. Como é que representa percursos «curvos»? Por exemplo, percursos circulares ou em onda. Leve a forma do anterior a percorrer um percurso em forma de:

   • Círculo.
   • Seno (ondas).
   • Curva x^3.
   • Um caminho poligonal com n pontos, definido por uma equação paramétrica.

3. Percursos Compostos. Como é que representa percursos definidos por várias «partes»? Por exemplo, um percurso como ilustrado na figura seguinte:

4. Percursos Acelerados. Repita o exercício dos percursos compostos, mas a forma:

   1. Acelera no início de cada segmento e trava no fim.
   2. Acelera no início do percurso e trava no fim.

Comportamentos

Exercício 3 - Seguidor

Implemente um comportamento seguidor.

Este comportamento consiste em controlar a posição de um objeto, o seguidor, de forma a coincidir com a posição de outro, o líder.

A forma mais simples consiste em, simplesmente, igualar a posição do seguidor à do líder:

follow.pos.x = leader.pos.x;
follow.pos.y = leader.pos.y;

Desta forma o movimento é abrupto e irrealista.

Uma forma melhor consiste em estabelecer uma velocidade máxima para o seguidor e, em vez de coordenadas cartesianas, usar coordenadas polares para dirigir o seguidor na direção do líder.

Isto é, para movimentar um objeto podemos usar coordenadas cartesianas. Usando um modelo simples inspirado na física, temos

pos.x = pos.x + vel.x * dt;
pos.y = pos.y + vel.y * dt;

mas é mais conveniente definir a velocidade (e a aceleração) em coordenadas polares:

// Update vel in polar coordinates: direction and "speed".
vel.a = ... ;   // direction
vel.d = ... ;   // speed (rapidez)

...

// Convert the velocity from polar to cartesian coordinates.
vel_cart = pol2cart(vel);
// Apply the "usual" position update.
pos.x = pos.x + vel_cart.x * dt;
pos.y = pos.y + vel_cart.y * dt;

Alínea a.

Defina o movimento do líder de forma a percorrer os quatro cantos da tela.

Use tweens para que esse movimento seja “natural”.

Implemente o movimento do líder usando tweens de forma a reduzir a velocidade antes de mudar de direção e acelerar depois.

Alínea b.

Defina o movimento do seguidor em termos de direção $a$ e rapidez $d$.

Use um valor constante para a rapidez e para a direção calcule

a = Math.atan2(leader.y - follow.y, leader.x - follow.x)

em que o líder está na posição {x: leader.x, y: leader.y} e o seguidor em {x: follow.x, y: follow.y}.

Implemente o movimento do seguidor em termos de coordenadas polares para a velocidade.

Alínea c.

Em vez da velocidade do seguidor ser constante, é mais interessante se depender da distância ao líder.

Implemente o movimento do seguidor de forma a que a velocidade seja proporcional à distância ao líder.

Alínea d.

Transforme este exercício num jogo de “apanhada”.

Em vez do movimento do líder ser controlado por tweens, use o teclado para o movimentar.

O código seguinte mostra como detetar eventos do teclado e definir efeitos em função da tecla pressionada. Neste caso, a direção do movimento do líder.

document.addEventListener("keydown", (e) => {
    switch (e.key) {
        case "d": case "D": leader.action = 1; break;   // RIGHT
        case "a": case "A": leader.action = 2; break;   // LEFT
        default: leader.action = 0; break;              // KEEP DIRECTION
    }
});

Adapte este exemplo de forma a controlar o movimento do líder usando as teclas d para “rodar o volante” para a direita e a para “rodar o volante” para a esquerda.

Alínea e.

Adapte o que fez a todos os sistemas gráficos.

Se tiver cuidado durante a implementação das alíneas anteriores, consegue separar a lógica de processamento do modelo das instruções específicas do sistema gráfico que está a usar.

1. Implemente uma “biblioteca” que faz toda a inicialização e atualização do modelo, independente de qualquer sistema gráfico.
2. Implemente “adaptadores” para cada sistema gráfico (SVG, C2D, X3D e 3JD).
3. Corra o “jogo” nos quatro sistemas em paralelo.

Exercício 4 - Bola Saltitona

Implemente uma bola saltitona.

Este comportamento consiste em movimentar uma bola num espaço limitado, aplicando (uma versão simplificada de) as leis da física:

Alínea a.

A posição $p$, a velocidade $v$ e a aceleração $a$ de um corpo estão relacionadas da seguinte forma: $$ \begin{aligned} a &= \frac{d}{dt} v &= \lim_{dt\to 0}\frac{v(t + dt) - v(t)}{dt} \cr v &= \frac{d}{dt} p &= \lim_{dt\to 0}\frac{p(t + dt) - p(t)}{dt} \end{aligned} $$

Se, em vez de $\lim_{dt \to 0}$, usarmos valores de $dt$ “muito pequenos” fica $$ \begin{aligned} a &= \frac{v(t + dt) - v(t)}{dt} \cr v &= \frac{p(t + dt) - p(t)}{dt} \end{aligned} $$ ou seja $$ \begin{aligned} v(t + dt) &= v(t) + a\times dt \cr p(t + dt) &= p(t) + v\times dt \end{aligned} $$

Estas equações permitem atualizar:

• A posição ($p(t + dt)$) a partir da posição anterior ($p(t)$) e da velocidade ($v$).
• A velocidade ($v(t + dt)$) a partir da velocidade anterior ($v(t)$) e da aceleração ($a$).

Ou seja, para descrever a evolução do movimento basta definir:

1. A posição inicial.
2. A velocidade inicial.
3. A aceleração ao longo do tempo.

Implemente uma animação do movimento de uma bola usando as equações acima, dadas condições iniciais para a posição e velocidade e aceleração constante.

Alínea b.

Num espaço limitado há colisões, que afetam a velocidade da bola. Se a bola está a deslocar-se para a direita a velocidade é, por exemplo, $v = (1, 0)$. Mas se a bola colidir com uma parede, passa a deslocar-se para a esquerda: $v = (-1, 0)$.

Implemente a colisão com paredes verticais e horizontais dadas as dimensões do espaço.

Alínea c.

Há várias forças que afetam o movimento da bola:

A força gravítica está sempre a influenciar o movimento para “baixo”. Isso significa que a bola está sempre sujeita a uma aceleração $$ g = G(0, 1) $$ em que $G$ é uma constante positiva e $(0, 1)$ é o vector que aponta para “baixo”.

A resistência aerodinâmica está sempre a contrariar o movimento da bola. Portanto a bola está sempre sujeita a uma aceleração $$ r = -R ||v||^2 \mathrm{vers}(v) $$ em que $R$ é uma constante positiva, $||v||$ é a norma da velocidade e $\mathrm{vers}(v)$ o seu versor.

Implemente as acelerações gravítica e resistência aerodinâmica dadas as contantes $G$ e $R$.

Alínea d.

Quando há uma colisão (por exemplo, com uma parede) parte da energia cinética da bola perde-se. Isso significa que nessa ocasião é aplicada uma aceleração $$ c = -C ||v||^2 \mathrm{vers}(v) $$ em que $C$ é uma constante positiva.

Um pontapé aplica uma aceleração súbita à bola. Pode-se simular um pontapé registando a posição de um click no espaço da bola e aplicando uma aceleração (1) na direção do click e (2) com intensidade proporcional à distância entre a bola e o click.

Se a bola está na posição $p$ e é registado um click na posição $q$ então nessa ocasião a aceleração a aplicar é:

$$ k = K || q - p || \mathrm{vers}(q - p) $$

em que $K$ é uma constante positiva.

Implemente as acelerações das colisões e dos pontapés dadas as contantes $C$ e $K$.

Integrações

Exercício 5 - Sistemas Gráficos

Animação em todos os sistemas gráficos.

Adapte o exercício do seguidor aos quatro sistemas gráficos: C2D, SVG, 3JS e X3D.

Alínea a.

Escreva o código das funções de inicialização (init) e atualização (update) do modelo de forma independente de qualquer sistema gráfico.

Alínea b.

Para cada um dos sistemas gráficos, escreva uma função de construção do modelo (render) adequada.

Alínea c.

Integre tudo de forma a mostrar a animação simultânea do modelo nos quatro sistemas gráficos.

Exercício 6 - Contágio

Simule um contágio.

Considere uma população de indivíduos que se deslocam ao acaso num espaço $\left[0,1\right] \times \left[0, 1\right]$ — tanto o $x$ como o $y$ variam entre $0$ e $1$. Cada indivíduo pode estar num de três estados:

• Saudável ($S$): Não contagia os vizinhos; mobilidade normal.
• Contagioso ($C$): Contagia os vizinhos; mobilidade normal.
• Doente ($D$): Contagia os vizinhos; sem mobilidade.

em que:

1. Um indivíduo com mobilidade normal desloca-se numa direção ao acaso.
2. O estado de um indivíduo evolui de acordo com probabilidades de transição de estado definidas na seguinte tabela: $$ \begin{array}{r|lll} & S & C & D \cr \hline S & 1.0 & 0.0 & 0.0 \cr C & 0.002 & 0.988 & 0.01 \cr D & 0.001 & 0.02 & 0.989 \end{array} $$ que descreve o seguinte:
   • Um indivíduo saudável (linha $S$) permanece saudável.
   • Um indivíduo contagioso (linha $C$) para para $S$ com probabilidade $0.002$;fica doente ($D$) com probabilidade $0.01$; permanece contagioso com a probabilidade restante.
   • Um individuo doente (linha $D$) fica $S$, $C$ com probabilidade $0.001$, $0.02$ e $0.5$ respetivamente.

• O contágio é transmitido aos vizinhos; cada vizinho $S$ de um indivíduo $C$ ou $D$ a uma distância inferior a $0.02$ (do tamanho do espaço) pode ficar $C$ com probabilidade $0.5$.

Alínea a.

Escreva o código das funções de inicialização (init_model) e atualização (update) do modelo de forma independente de qualquer sistema gráfico.

Alínea b.

Adicione obstáculos.

Alínea c.

Acrescente um gráfico que mostra a evolução das populações $S/C/D$ ao longo do tempo.

Alínea d.

Acrescente inputs para os parâmetros da simulação: probabilidades de transição de estado; população inicial; distância de contágio; etc.

Recursos

• C2D
• SVG
• X3D
• 3JS
• Tweenjs

Recursos C2D

Referências

• Norma em HTML Canvas 2D Context e WHATWG - HTML Living Standard.
• Documentação em Mozilla Developer Network.
• Tutorial em Mozilla Developer Network.

Modelos

Para documentos «pequenos», por exemplo, para testar uma função ou técnica, pode usar um único documento HTML com o código gráfico incluído.

Porém, se está a fazer um modelo gráfico mais complexo, deve separar o documento HTML do código JavaScript em vários ficheiros .

Um documento «standalone>

O código JavaScript está incluído no documento HTML.

<!DOCTYPE html>
<html>
<head>
    <meta charset="utf-8" />
    <script>
function main() {
    let gc = document
        .getElementById("acanvas")
        .getContext("2d");
    gc.fillStyle = "steelblue";
    gc.fillRect(0,0,256,256);
}
    </script>
</head>
<body>
    <canvas id="acanvas">
        <script>main();</script>
    </canvas>
</body>
</html>

Código e Documento separados

O código JavaScript está separado do documento HTML.

Ficheiro HTML:

<!DOCTYPE html>
<html>
<head>
    <meta charset="utf-8" />
    <script src="prog.js">
    </script>
</head>
<body>
    <canvas id="c2d:canvas"></canvas>
    <script>main("c2d:canvas");</script>
</body>
</html>

Ficheiro prog.js com código JavaScript:

function main(target_id) {
    let gc = document
                .getElementById(target_id)
                .getContext("2d");
    gc.fillStyle = "steelblue";
    gc.fillRect(0,0,256,256);
}

Recursos SVG

Documentação

• Norma em Scalable Vector Graphics (SVG) 1.1 (Second Edition).
• Documentação em Mozilla Developer Network.
• Tutorial em W3C: An SVG Primer for Today’s Browsers.
• Lista de Nomes de Cores CSS.

Modelos Base

Para documentos «pequenos», por exemplo, para testar uma função ou técnica, pode usar um único documento SVG que pode ser visualizado em vários programas, incluindo browsers, o VSCodium, etc.

Porém, se o seu modelo gráfico faz parte de um documento HTML pode colocar o elemento SVG diretamente embebido no documento HTML.

Um documento «standalone»

Um modelo gráfico SVG pode ficar guardado num único ficheiro, com extensão svg, e ser visualizado por vários programas.

<!DOCTYPE svg PUBLIC 
    "-//W3C//DTD SVG 1.1//EN" 
    "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="..." height="..."
    xmlns="http://www.w3.org/2000/svg"
    xmlns:xlink="http://www.w3.org/1999/xlink">
    <!-- conteúdo do documento SVG -->
</svg>

Um documento «embebido»

Num documento HTML (ou outro…), é possível embeber diretamente conteúdo SVG com:

<svg width="..." height="..."
    xmlns="http://www.w3.org/2000/svg"
    xmlns:xlink="http://www.w3.org/1999/xlink">
    <!-- conteúdo do elemento SVG -->
</svg>

Recursos X3D

Documentação

• Norma em X3D® version 4 (X3D4) Architecture Specification.
• Documentação em Official x3dom Documentation.
• Tutorial em W3C: x3dom Tutorials.
• Versão estável mais recente (download).

Modelos

Os modelos abaixo funcionam assumindo que:

1. Fez o download recomendado;
2. O arquivo zip foi descompactado para a pasta lib/ da sua diretoria de trabalho;

Isto é, deve obter a seguinte àrvore:

(directoria de trabalho)/
    lib/
        x3dom/
            doc/
                (vários ficheiros)
            (vários ficheiros)
            x3dom.js
            x3dom-full.js
            x3dom.css
    (os seus ficheiros de trabalho)

Um documento «standalone»

<!DOCTYPE html>
<html lang="pt">
<head>
    <meta charset="utf8">
    <title>Standalone X3D</title>
    <script 
        type='application/javascript' 
        src='./lib/x3dom/x3dom-full.js'>
    </script>
    <link 
        rel='stylesheet' 
        type='text/css' 
        href='./lib/x3dom/x3dom.css' />
</head>

<body>
    <X3D>
        <Scene>
            <Shape>
                <Appearance>
                    <Material 
                        diffuseColor="crimson">
                    </Material>
                </Appearance>
                <Cylinder></Cylinder>
            </Shape>
        </Scene>
    </X3D>
</body>
</html>

Modelo e Documento separados

Parte HTML (Documento)

Ficheiro documento.html:

<!DOCTYPE html>
<html lang="pt">
<head>
    <meta charset="utf8">
    <title>Modelo + Documento X3D</title>
    <script 
        type='application/javascript' 
        src='./lib/x3dom/x3dom-full.js'>
    </script>
    <link 
        rel='stylesheet' 
        type='text/css' 
        href='./lib/x3dom/x3dom.css' />
</head>

<body>
    <div>
        <X3D width="512px" height="512px">
            <Scene>
              <Inline url="modelo.x3d"></Inline>
            </Scene>
        </X3D>
    </div>
</body>
</html>

Parte X3D (Modelo)

Ficheiro modelo.x3d:

<X3D>
    <Scene>
        <Shape>
            <Appearance>
                <Material diffuseColor="crimson">
                </Material>
            </Appearance>
            <Cylinder></Cylinder>
        </Shape>
    </Scene>
</X3D>

Geometria por Faces

Geometria sem mapa UV

Uso simples de IndexedFaceSet.

<Shape>
    <Appearance>
            <Appearance>
                <Material diffuseColor="crimson">
                </Material>
            </Appearance>
    </Appearance>
    <IndexedFaceSet coordIndex="
        [ FACES: indices dos VÉRTICES seguido de -1 para 'terminar' cada face  ]
        ">
        <Coordinate point="
            [ VÉRTICES: coordenadas XYZ ]
            ">
        </Coordinate>
    </IndexedFaceSet>
</Shape>

Geometria com mapa UV

Veja como obter mapas de reflexos e de normais em NormalMap-Online.

<Shape>
    <Appearance>
        <CommonSurfaceShader>
            <ImageTexture
                containerField="diffuseTexture" 
                url="[mapa de DIFUSÃO]"></ImageTexture>
            <ImageTexture
                containerField="specularTexture"
                url="[mapa de REFLEXOS]"></ImageTexture>
            <ImageTexture
                containerField="normalTexture"
                url="[mapa de NORMAIS]"></ImageTexture>
        </CommonSurfaceShader>
    </Appearance>
    <IndexedFaceSet coordIndex="
        [ FACES: indices dos VÉRTICES seguido de -1 para 'terminar' cada face  ]
        "
        texcoordIndex="        
        [ SETORES: indices dos PONTOS seguido de -1 para 'terminar' cada setor ]
        ">
        <Coordinate point="
            [ VÉRTICES: coordenadas XYZ ]
            ">
        </Coordinate>
        <TextureCoordinate point="
            [ PONTOS: coordenadas UV ]
            ">
        </TextureCoordinate>
    </IndexedFaceSet>
</Shape>

Atalhos de teclado

Recursos 3JS (aka three.js)

Referências

• Página: https://threejs.org
• Documentação em threejs.org.
• Manual em threejs.org.
• Exemplos em threejs.org.
• Downloads
  • Para Computação Gráfica; ← recomendado!
  • Do repositório oficial do threejs.org; (pode ser um ficheiro de tamanho substancial)
• Documentação Javascript relevante:
  • módulos;
  • scriptmap;

Modelos

Os modelos abaixo funcionam assumindo que:

1. Fez o download recomendado;
2. O arquivo zip foi descompactado para a pasta lib/ da sua diretoria de trabalho;

Isto é, deve obter a seguinte àrvore:

(directoria de trabalho)/
    lib/
        threejs/
            build/
                (vários ficheiros)
            addons/
                jsm/
                    (vários ficheiros)
    (os seus ficheiros de trabalho)

Um documento «standalone>

<!DOCTYPE html>
<html lang="en">
	<head>
		<title>3JS Embebido</title>
		<meta charset="utf-8">
		<script type="importmap">
			{
				"imports": {
					"three": "./lib/threejs/build/three.module.js",
					"three/addons/": "./lib/threejs/addons/jsm/"
				}
			}
		</script>
	</head>

	<body>
		<div id="3js:container">
		</div>

		<script type="module">
// Bibliotecas			
import * as THREE from 'three';
import { OrbitControls } from 'three/addons/controls/OrbitControls.js';

// Elemento HTML com o modelo gráfico
const container = document.getElementById("3js:container");
container.width = 512;
container.height = 512;

// Construtor (Renderer) do modelo gráfico
const renderer = new THREE.WebGLRenderer( {alpha: true} );
renderer.setPixelRatio( window.devicePixelRatio );
renderer.setSize(
	container.width,
	container.height );
renderer.setClearColor("khaki", 0.25);	
// Ligar elemento <-> construtor
container.appendChild(renderer.domElement);

// Câmara para observar o modelo
const camera = new THREE.PerspectiveCamera(
	35,       // abertura
	container.width/container.height,  // proporção largura/altura
	0.1,      // corte perto
	10000     // corte longe
	);
camera.position.set( -2.5, 0, 20 );

// Controlos da câmara
const controls = new OrbitControls( 
	camera, 
	renderer.domElement );

// Cena do modelo (raiz)
const scene = new THREE.Scene();
// Orientar a câmara para a cena
camera.lookAt(scene.position);

// Uma geometria (caixa)
const geometry = new THREE.BoxGeometry( 5, 5, 5 );
// Um material (cor)
const material = new THREE.MeshLambertMaterial( {color: "steelblue"} );
// Um objecto gráfico (geometria + material)
const mesh = new THREE.Mesh( geometry, material );
// Ligar cena <-> objecto gráfica
scene.add( mesh );

// Uma luz
const light = new THREE.AmbientLight( "white" );
// Ligar cena <-> luz
scene.add( light );

// Processo da animação
function animate() {
	controls.update();              // Atualizar os controlos
	mesh.rotation.y += 0.01;        // Atualizar o modelo
	renderer.render(scene, camera); // Construir a cena atualizada
}

renderer.setAnimationLoop( animate );	// Ligar animação <-> construtor
		</script>
	</body>
</html>

Código e Documento separados

Parte HTML (Documento)

Atenção ao seguinte:

• A linha "prog": "./prog.js" no importmap define o nome "prog" para importar o código que está no ficheiro ./prog.js.

• No segundo elemento script:

  • O tipo module, necessário para se utilizar sistema de módulos da Javascript;
  • A instrução import main from "prog": na primeira linha desse elemento: Esta instrução importa para este elemento o código referido pelo nome "prog" definido no importmap acima.

Ficheiro doc.html:

<!DOCTYPE html>
<html lang="en">
	<head>
		<title>Modelo + Documento 3JS</title>
		<meta charset="utf-8">
		<script type="importmap">
			{
				"imports": {
					"three": "./lib/threejs/build/three.module.js",
					"three/addons/": "./lib/threejs/addons/jsm/",

					"prog": "./prog.js"
				}
			}
		</script>
	</head>

	<body>
		<div id="3js:container">
		</div>

		<script type="module">
			import main from "prog";
			main("3js:container");
		</script>

	</body>
</html>

Parte Javascript (Programa)

Atenção: A declaração export default fucntion main() (em prog.js) é necessária para permitir-se o acesso «externo» a esta função.

Ficheiro prog.js

// Bibliotecas			
import * as THREE from 'three';
import { OrbitControls } from 'three/addons/controls/OrbitControls.js';

export default function main(container_id) {
	// Elemento HTML com o modelo gráfico
	const container = document.getElementById(container_id);
	container.width = 512;
	container.height = 512;

	// Construtor (Renderer) do modelo gráfico
	const renderer = new THREE.WebGLRenderer({ alpha: true });
	renderer.setPixelRatio(window.devicePixelRatio);
	renderer.setSize(
		container.width,
		container.height);
	renderer.setClearColor("khaki", 0.25);
	// Ligar elemento <-> construtor
	container.appendChild(renderer.domElement);

	// Câmara para observar o modelo
	const camera = new THREE.PerspectiveCamera(
		35,       // abertura
		container.width / container.height,  // proporção largura/altura
		0.1,      // corte perto
		10000     // corte longe
	);
	camera.position.set(-2.5, 0, 20);

	// Controlos da câmara
	const controls = new OrbitControls(
		camera,
		renderer.domElement);

	// Cena do modelo (raiz)
	const scene = new THREE.Scene();
	// Orientar a câmara para a cena
	camera.lookAt(scene.position);

	// Uma geometria (caixa)
	const geometry = new THREE.BoxGeometry(5, 5, 5);
	// Um material (cor)
	const material = new THREE.MeshLambertMaterial({ color: "steelblue" });
	// Um objecto gráfico (geometria + material)
	const mesh = new THREE.Mesh(geometry, material);
	// Ligar cena <-> objecto gráfica
	scene.add(mesh);

	// Uma luz
	const light = new THREE.AmbientLight("white");
	// Ligar cena <-> luz
	scene.add(light);

	// Processo da animação
	function animate() {
		controls.update();					// Atualizar os controlos
		mesh.rotation.y += 0.01;			// Atualizar o modelo
		renderer.render(scene, camera);		// Construir a cena atualizada
	}

	renderer.setAnimationLoop(animate);	// Ligar animação <-> construtor
}

Geometria por Faces

A classe central é a BufferGeometry.

Geometria sem mapa UV

function IndexedFaceSet(vertices, faces) {
    //
    //  Geometry: "Indexed Face Set"
    //
    //  Generate all the vertexes in the XYZ plane
    const positions = [];
    for (const i of faces) {
        const xyz_point = vertices.slice(3 * i, 3 * i + 3);
        positions.push(...xyz_point);
    }
    //
    const geo = new THREE.BufferGeometry();
    //
    geo.setAttribute("position",
        new THREE.Float32BufferAttribute(positions, 3));
    //
    geo.computeBoundingSphere();
    //
    return geo;
}

Geometria e Mapa UV

Veja como obter mapas de reflexos e de normais em NormalMap-Online.

O three.js suporta geometrias definidas por faces, e aplicação de texturas por mapas uv. A função seguinte define uma geometria por faces com um mapa UV.

function IndexedFaceUVSet(vertices, faces, points, sectors) {
    //
    //  Geometry: "Indexed Face UV Set"
    //
    //  Generate all the vertexes in the XYZ plane
    const positions = [];
    for (const i of faces) {
        const xyz_point = vertices.slice(3 * i, 3 * i + 3);
        positions.push(...xyz_point);
    }
    //
    //  Generate all the points in the UV plane 
    const uvs = [];
    for (const i of sectors) {
        const uv_point = points.slice(2 * i, 2 * i + 2);
        uvs.push(...uv_point);
    }
    //
    const geo = new THREE.BufferGeometry();
    //
    geo.setAttribute("position",
        new THREE.Float32BufferAttribute(positions, 3));
    geo.setAttribute("uv",
        new THREE.Float32BufferAttribute(uvs, 2));
    //
    geo.computeVertexNormals();
    geo.computeBoundingSphere();
    //
    return geo;
}

Textura com mapas de difusão, reflexos e normais

Os materiais do tipo MeshPhongMaterial suportam mapas de difusão, reflexos e normais.

const textureLoader = new THREE.TextureLoader();

const diffuseMap = textureLoader.load('[ mapa de DIFUSÃO ]');
const specularMap = textureLoader.load('[ mapa de REFLEXOS ]');
const normalMap = textureLoader.load('[ mapa de NORMAIS ]');

const material = new THREE.MeshPhongMaterial( {
	map: diffuseMap,
	specularMap: specularMap,
	normalMap: normalMap
} );

Recursos Tween.js

Referências

• Documentação no repositório.
• Guia do Utilizador no repositório.
• Instalação
  • Para Computação Gráfica ← recomendado!
  • Instruções do repositório

Modelos

Os modelos abaixo funcionam assumindo que:

1. Fez o download recomendado;
2. O arquivo zip foi descompactado para a pasta lib/ da sua diretoria de trabalho;

Isto é, deve obter a seguinte árvore:

(directoria de trabalho)/
    lib/
        tweenjs/
            (vários ficheiros)
    (os seus ficheiros de trabalho)

Um documento «standalone>

O código JavaScript está incluído no documento HTML.

<!DOCTYPE html>
<html>
<head>
    <meta charset="utf-8" />
    <script type="importmap">
        {
            "imports": {
                "tween": "./lib/tweenjs/tween.esm.js"
            }
        }
    </script>
</head>
<body>
    <div id="target"></div>
    <script type="module">
        import {Tween} from "tween";
        
        const target = document.getElementById("target");
        const value = { x: 0.0 };
        const tween = new Tween(value)
            .to({x: 10.0}, 5000)
            .onUpdate(v => target.innerText = `Got: ${v.x.toPrecision(2)}` )
            .yoyo(true)
            .repeat(Infinity)
            .start();

        const step = () => {
            tween.update();
            requestAnimationFrame(step);
        }

        step();
    </script>
</body>
</html>

Código e Documento separados

O código JavaScript está separado do documento HTML.

Ficheiro HTML:

<!DOCTYPE html>
<html>
<head>
    <meta charset="utf-8" />
    <script type="importmap">
        {
            "imports": {
                "tween": "./lib/tweenjs/tween.esm.js",
                "prog": "./prog.js"
            }
        }
    </script>
</head>
<body>
    <div id="target"></div>
    <script type="module">
        import main from "prog";

        main("target");
    </script>
</body>
</html>

Ficheiro prog.js com código JavaScript:

import { Tween } from "tween";

export { main as default };

function main(target_id) {
    const target = document.getElementById(target_id);
    const value = { x: 0.0 };
    const tween = new Tween(value)
        .to({ x: 10.0 }, 5000)
        .onUpdate(v => target.innerText = `Got: ${v.x.toPrecision(2)}`)
        .yoyo(true)
        .repeat(Infinity)
        .start();

    const step = () => {
        tween.update();
        requestAnimationFrame(step);
    }

    step();
}

Uma Cadeia de Tweens

Ficheiro HTML:

<!doctype html>
<html>
    <head>
        <meta charset="utf-8" />
        <script type="importmap">
            {
                "imports": {
                    "tween": "./lib/tweenjs/tween.esm.js",
                    "prog": "./tweens-chain.js"
                }
            }
        </script>
    </head>
    <body>
        <canvas id="tweens:target"></canvas>
        <script type="module">
            import main from "prog";
            main("tweens:target");
        </script>
    </body>
</html>

Ficheiro tweens-chain.js com código JavaScript:

import { Tween, Group } from "tween";

export { main as default };

function draw(c, m) {
  c.fillStyle = "khaki";
  c.fillRect(0, 0, 512, 512);
  c.fillStyle = "crimson";
  c.fillRect(m.x, m.y, 32, 32);
}

function main(target_id) {
  const context = document.getElementById(target_id).getContext("2d");
  context.canvas.width = 512;
  context.canvas.height = 512;

  const model = { x: 8, y: 8 };
  const right = new Tween(model).to({ x: 472 }, 1000);
  const down = new Tween(model).to({ y: 472 }, 1000);
  const left = new Tween(model).to({ x: 8 }, 1000);
  const up = new Tween(model).to({ y: 8 }, 1000);

  right.chain(down);
  down.chain(left);
  left.chain(up);
  up.chain(right);

  const group = new Group();
  group.add(right, down, left, up);
  right.start();

  const step = () => {
    group.update();
    draw(context, model);
    requestAnimationFrame(step);
  };

  step();
}

Exemplos

Seguidor Interativo

Controle um líder (o quadrado vermelho) usando as teclas QAOP para fugir de um seguidor (o quadrado azul) e evitar colidir com as paredes.

Este exemplo ilustra o ciclo de animação:

let model = init_model();
let context = new_context();
let step = (ts) => { 
  model.update(ts);
  context.render(model);
  requestAnimationFrame(step);
}

requestAnimationFrame(step);

Em particular, os seguintes pontos:

• Usar um modelo para controlar uma animação por passos.
• Atualizar o modelo em função de eventos «externos». Neste caso, eventos do teclado.
• Aplicar conversões entre coordenadas cartesianas e polares para facilitar o controlo do movimento de um objeto gráfico.
• Fazer o movimento em termos de aceleração, velocidade e posição.

O Modelo

Um modelo tem um estado inicial que é atualizado ao longo da animação.

1. O modelo é inicializado na função init_model — esta função define um objeto com os parâmetros necessários para a animação, mais alguns usados na visualização e acrescenta alguns métodos a esse objeto para tornar a programação da animação mais sistemática e ergonómica.
2. O modelo é atualizado em cada passo da animação através do método update.
3. A evolução do modelo depende de eventos externos, que são detetados assincronamente e processados durante a atualização.

Estado Inicial

Na construção do estado inicial são definidos os atributos e métodos que definem o modelo.

Esta animação tem um leader controlado com o teclado, e um follower que procura «apanhar» o líder. Portanto, o modelo necessita de parâmetros e métodos para:

• Representar a posição das «personagens».
• Aplicar as ações que decorrem do teclado.
• Atualizar o modelo.
• Proporcionar propriedades de visualização como «cor» ou «tamanho»

Movimento

Para controlar o movimento dos objetos define-se uma posição pos: {x:, y:} e uma velocidade vel: {x:, y:}.

function init_model() {
  const model = {
    age: 0,
    leader: {
      pos: { x: 8, y: 8 },
      vel: { x: 0, y: 0 },
      size: 16,
      color: "crimson",
      A: 1000,
    },
    follower: {
      pos: { x: 128, y: 128 },
      vel: { x: 0, y: 0 },
      max_speed: 50,
      size: 8,
      color: "steelblue",
    },
    background: "khaki",
    width: 256,
    height: 256,
    action: 0,
  };
  
  // Further model definitions
  
  return model;
}

Adicionalmente, o modelo tem os seguintes atributos:

• age é o número de passos decorridos desde que a animação iniciou.
• background, width e height definem propriedades visuais da animação (côr de fundo, largura e altura).
• action representa a ação a ser executada no passo atual. Por exemplo, «subir», «descer», etc. — o valor deste parâmetro é definido assincronamente quando o utilizador pressiona uma tecla e posteriormente processado para definir a aceleração do leader.

Controlo por Teclado

O movimento do leader é controlado pelas teclas QAOP (o S tem de ser evitado pois já é usado para fazer pesquisas).

Este controlo tem duas fases:

1. Deteção assíncrona do evento de teclado;
2. Atualização adequada do modelo, durante a fase update.

Para a deteção assíncrona usa-se o método document.addEventListener (veja a respetiva documentação aqui):

function init_model() {
  const model = {
    ...
  };

  document.addEventListener("keydown", (e) => {
    switch (e.key) {
      case "Q":
      case "q": // UP
        model.action = 1;
        break;
      case "A":
      case "a": // DOWN
        model.action = 2;
        break;
      case "P":
      case "p": // RIGHT
        model.action = 3;
        break;
      case "O":
      case "o": // LEFT
        model.action = 4;
        break;
      case "r":
      case "R": // RESET
        model.action = 5;
        break;
      default: // NOOP
        model.action = 0;
        break;
    }
  });
  
  // Further model definitions
  
  return model;
}

Esta instrução faz com seja executada uma certa ação cada vez que é pressionada ("keydown") alguma daquelas teclas (QAOP e R). Neste caso essa ação é apenas definir o valor do parâmetro model.action de forma que:

Aqui pretende-se apenas detetar e registar o evento externo. As instruções a executar neste passo devem evitar cálculos prolongados. Para o registo do evento usa-se o parâmetro model.action que será devidamente processado durante a atualização (update) do modelo.

Tempos e Atualização

Os restantes atributos do modelo representam (1) momentos «importantes» e (2) o método de atualização.

function init_model() {
  const model = { ...
  };

  document.addEventListener("keydown", (e) => {...
  });

  model.start = performance.now();
  model.last_ts = model.start;

  model.update = update;

  return model;
}

O atributo model.last_ts é atualizado em cada passo da animação e regista o momento em que esse passo foi executado. Esta informação é importante para determinar o tempo decorrido desde o passo anterior.

Atualização do Modelo

A atualização do modelo é implementada no método update e segue uma determinada sequência.

1. Atualização dos tempos — deste o passo anterior; número de passos, etc.
2. Aplicação das ações — o valor do parâmetro model.action determina a aceleração a aplicar ao leader.
3. Velocidade, posição e colisões do leader — a aceleração aplicada vai determinar a velocidade e, esta, a posição. Porém, o leader pode colidir com os limites do modelo, pelo que é necessário detetar essas colisões e fazer as correções apropriadas.
4. Velocidade e posição do follower — a nova posição do leader determina um novo rumo para o follower; esse cálculo é mais simples usando coordenadas polares.

Programação por Objetos em JavaScript

Um aspeto importante da programação JavaScript é o uso do termo reservado this e o uso de algumas caraterísticas de programação por objetos; nomeadamente, o uso de métodos.

Na linguagem JavaScript é possível acrescentar atributos e métodos a objetos:

const target = document.getElementById("js:oop");
function greet(prompt) {                    // "this" is a owner of this method.
    target.innerText = `${prompt} ${this.name} ${this.surname}!`;
}
const person = { name: "John", age: 34 };   // Object
person.surname = "Doe";                     // Add an attribute
person.greet = greet;                       // Add a method
person.greet("Hi there");                   // Use the method

O aspeto chave deste exemplo é o uso do termo reservado this na definição da função/método greet — é uma referência ao objeto que tem esse método.

Atualização dos Tempos

Para a animação por passos é necessário que a função de atualização do modelo tenha como entrada informação sobre o tempo.

Neste caso é usado o protocolo do método requestAnimationFrame(callback) (documentação) em que a função callback tem um único argumento timestamp; o momento em que o callback está a ser executado pelo requestAnimationFrame.

let step = (ts) => { 
  model.update(ts);
  context.render(model);
  requestAnimationFrame(step);
}
requestAnimationFrame(step);

O método de atualização do modelo é:

function update(ts) {
  this.age += 1;
  const dt = 0.001 * (ts - this.last_ts);
  this.last_ts = ts;

  // Further update instructions
}

O argumento ts é o timestamp (carimbo temporal; «agora» em milisegundos) e as primeiras instruções tratam do progresso do tempo:

• this.age += 1; incrementa a «idade» do modelo;
• As restantes duas instruções determinam:
  • O tempo decorrido deste o passo anterior (dt).
  • Atualizam o registo do momento do passo this.last_ts = ts.

Aplicação de Ações (Eventos Externos)

Estas instruções usam a representação da ação, this.action definida durante a deteção de eventos, para atualizar o modelo.

function update(ts) {
  // Previous instructions

  const a = { x: 0, y: 0 };
  switch (this.action) {
    case 1: // UP
      a.y = -1.0;
      break;
    case 2: // DOWN
      a.y = 1.0;
      break;
    case 3: // RIGHT
      a.x = 1.0;
      break;
    case 4: // LEFT
      a.x = -1.0;
      break;
    case 5: // RESET
      // Homework: Reset the model
      break;
    case 0:
    default:
      break;
  }
  this.action = 0;  // Experiment: remove this instruction!

  // More instructions
}

Neste caso a atualização consiste em aplicar uma aceleração ao leader. Essa aceleração é um vetor a = {x:, y:} que, consoante a ação, define um movimento para a esquerda, direita, cima ou baixo.

A instrução

  this.action = 0;  // Experiment: remove this instruction!

faz com que uma ação definida num passo de atualização fique limitada a esse passo.

Experimente remover esta instrução e observe o efeito no movimento do leader.

Velocidade, Posição e Colisões do Líder

A ação this.action define a aceleração, a, a aplicar ao leader. Segue-se a atualização da velocidade e posição do leader, tendo em conta as leis do movimento e as colisões com os limites do modelo.

As leis do movimento são: $$ \left\lbrace \begin{aligned} v & \gets v + a \delta_t, \cr p & \gets p + v \delta_t \end{aligned} \right. $$

A atualização das componentes horizontais (x) é feita com as seguintes instruções:

function update(ts) {
  // Previous instructions
  
  //
  // LEADER X update
  // 
  // vel.x
  this.leader.vel.x += this.leader.A * a.x * dt;
  // pos.x
  this.leader.pos.x += this.leader.vel.x * dt;
  // collision with the right wall
  if (this.leader.pos.x > this.width - this.leader.size) {
    this.leader.pos.x = this.width - this.leader.size;
    this.leader.vel.x = 0;
  }
  // collision with the left wall
  if (this.leader.pos.x < 0) {
    this.leader.pos.x = 0;
    this.leader.vel.x = 0;
  }
  //
  // LEADER Y update
  // 
  // Analogous to LEADER X update
  
  // More instructions
}

A atualização da posição horizontal começa no «bloco» LEADER X update:

1. A aceleração horizontal atualiza a velocidade horizontal.
2. A velocidade horizontal atualiza a posição horizontal.
3. São testadas as colisões horizontais e, se necessário, ajustadas as velocidade e posição horizontais.

Mais especificamente, a linha

  this.leader.vel.x += this.leader.A * a.x * dt;

atualiza a velocidade por aplicação da lei

$$ v \gets v + a \delta_t $$

usando a aceleração e o tempo decorrido: a.x * dt. O parâmetro this.leader.A serve apenas para aumentar o efeito da aceleração.

Experimente fazer model.leader.A: 1 na função init_model e observe o efeito no movimento do leader.

A atualização da posição horizontal é feita em

  this.leader.pos.x += this.leader.vel.x * dt;

que aplica

$$ p \gets p + v \delta_t. $$

Esta atualização pode ter criado uma colisão com uma parede. As colisões (horizontais) são detetadas em

function update(ts) {
  // Previous instructions
  
  // collision with the right wall
  if (this.leader.pos.x > this.width - this.leader.size) {
    ...
  }
  // collision with the left wall
  if (this.leader.pos.x < 0) {
    ...
  }
  
  // More instructions
}

e, quando é detetada uma colisão, o leader:

1. É parado (na direção da colisão): this.leader.vel.x = 0;.
2. É colocado «dentro» da área do modelo: this.leader.pos.x = ...;.

A atualização da velocidade e da posição verticais (LEADER Y update) é análoga:

1. A aceleração atualiza a velocidade.
2. A velocidade atualiza a posição.
3. São testadas as colisões e, se necessário, ajustadas a posição e a velocidade.

Velocidade e Posição do Seguidor

O follower (seguidor) desloca-se na direção do leader mas tem a velocidade limitada a um valor máximo (model.follower.max_speed).

Portanto, para determinar em que direção o follower se desloca, assim como a sua velocidade, é mais conveniente usarem-se coordenadas polares. A conversão entre coordenadas cartesianas (usadas no modelo) e polares usa as seguintes funções:

function cart2polar(p) {
  return {
    a: Math.atan2(p.y, p.x),
    d: Math.hypot(p.x, p.y),
  };
}

function polar2cart(q) {
  return {
    x: q.d * Math.cos(q.a),
    y: q.d * Math.sin(q.a),
  };
}

A direção (cartesiana) do ponto p para o ponto q e a respetiva distância são:

function dir(p, q) {
  return {
    x: q.x - p.x,
    y: q.y - p.y,
  };
}

function dist(p, q) {
  return Math.hypot(q.x - p.x, q.y - p.y);
}

Agora a atualização da velocidade e posição do seguidor é:

function update(ts) {
  // Previous instructions
  
  // FOLLOWER
  //
  // Heading
  const follower_heading_cart = dir(this.follower.pos, this.leader.pos);
  const follower_heading_pol = cart2polar(follower_heading_cart);
  //
  // Speed proportional to distance to leader
  // but limited by this.follower.max_speed
  follower_heading_pol.d = Math.min(
    this.follower.max_speed,
    dist(this.follower.pos, this.leader.pos),
  );
  //
  // Cartesian vel
  this.follower.vel = polar2cart(follower_heading_pol);
  //
  // Position update
  this.follower.pos.x += this.follower.vel.x * dt;
  this.follower.pos.y += this.follower.vel.y * dt;
}

Com a instrução

  follower_heading_pol.d = Math.min(
    this.follower.max_speed,
    dist(this.follower.pos, this.leader.pos),
  );

a velocidade fica proporcional à distância entre o follower e o leader mas limitada por model.follower.max_speed.

A Visualização

A visualização do modelo consiste na construção (render) de uma imagem em cada passo da animação.

Usa-se o sistema C2D (i.e. o CanvasRenderingContext2D), acrescentando métodos específicos para a construção deste modelo.

As propriedades gráficas das «peças» desta animação são definidas pelos atributos

{
  pos: {x: ..., y: ... },
  size: ... ,
  color: ...,
}

Os métodos de visualização são:

function render_piece(c) {
  this.fillStyle = c.color;
  this.fillRect(c.pos.x, c.pos.y, c.size, c.size);
}

function render_c2d(m) {
  this.write(`AGE: ${m.age}`);
  this.fillStyle = m.background;
  this.fillRect(0, 0, m.width, m.height);

  this.render_piece(m.leader);
  this.render_piece(m.follower);
}

O método this.write(...) «ainda» não está definido. Este método serve para escrever mensagens de texto num «terminal» de forma a proporcionar alguma informação não visual sobre a evolução do modelo.

O sistema gráfico (e o modelo) é inicializado da seguinte forma:

function main(target_c2d, target_terminal) {
  const model = init_model();

  const context_c2d = document.getElementById(target_c2d).getContext("2d");
  context_c2d.canvas.width = model.width;
  context_c2d.canvas.height = model.height;
  
  context_c2d.render = render_c2d;
  context_c2d.render_piece = render_piece;

  const terminal = document.getElementById(target_terminal);
  context_c2d.write = (text) => (terminal.innerHTML = text);

  // More instructions
}

A instância context_c2d é aumentada com os métodos seguintes:

  ...
  context_c2d.render = render_c2d;
  context_c2d.render_piece = render_piece;
  ...
  context_c2d.write = (text) => (terminal.innerHTML = text);
  ...

que proporcionam:

• A construção (render) do modelo: context_c2d.render.
• A construção (render) de cada «peça»: context_c2d.render_piece.
• Um sistema de mensagens de texto: context_c2d.write.

O Ciclo de Animação

O ciclo de animação inclui a atualização seguida da visualização do modelo e é definido pela função step.

function main(target_c2d, target_terminal) {
  // Previous instructions

  const step = function (ts) {
    model.update(ts);
    context_c2d.render(model);
    requestAnimationFrame(step);
  };

  requestAnimationFrame(step);
}

1. A instrução model.update(ts); usa o método update acrescentado a model em init_model;
2. Em context_c2d.render(model) o modelo é visualizado pelos métodos acrescentados ao contexto gráfico context_c2d.
3. A primeira instrução requestAnimationFrame(step); torna a executar a função step quando o browser atualizar a página.
4. A segunda instrução requestAnimationFrame(step); inicia a animação.

A Parte HTML

A animação «existe» num documento HTML.

<script type="importmap">
  {
    "imports": {
      "tween": "./lib/tweenjs/tween.esm.js",
      "follower": "./follower.js"
    }
  }
</script>

<div style="display: grid; grid-template-columns: 256px 256px">
    <canvas id="c2d:canvas"></canvas>
    <div id="terminal" style="font-family:monospace;padding:0.5em;background:black;color:seagreen">TERMINAL</div>
</div>

<script type="module">
    import main from "follower";
    main("c2d:canvas", "terminal");
</script>

O Que Falta (Exercícios)

• Adicione «energia» ao leader: cada vez que colide com uma parede perde alguma energia; se for «apanhado» pelo seguidor perde mais energia;
• Aumente a dificuldade: Adicione novos seguidores de x em x segundos;
• Acrescente PowerUps: O contrário dos seguidores; fogem do leader mas dão pontos quando «apanhados».
• Junte «obstáculos»: objetos estacionários e incontornáveis que tornam a vida do leader mais interessante.
• Implemente adaptações para outros sistemas gráficos sem alterar o modelo.

Visualizações Simultâneas

Visualize simultaneamente um modelo em vários sistemas gráficos.

TERMINAL

Este exemplo ilustra a animação de um modelo em quatro sistemas gráficos:

const terminal = document.getElementById(target_terminal);
const write = (text) => {
  terminal.innerText = text;
};

const model = init_model();

const context_c2d = new_context_c2d(target_c2d, model);
const context_svg = new_context_svg(objects_svg);
const context_x3d = new_context_x3d(objects_x3d);
const context_3js = new_context_3js(target_3js, model);

const step = function (ts) {
  model.update(ts);
  write(`AGE: ${model.age}`);
  context_c2d.render(model);
  context_svg.render(model);
  context_x3d.render(model);
  context_3js.render(model);

  requestAnimationFrame(step);
};

requestAnimationFrame(step);

Em particular:

• O modelo usa um controlo por tempo (para o leader vermelho) e um controlo por passos (para o follower azul).
• O modelo é atualizado em cada passo da animação através do método update.
• A visualização é feita simultaneamente em quatro sistemas gráficos, C2D, SVG, 3JS e X3D.
• Adicionalmente, aqui também se ilustra como organizar o código, separando-o por bibliotecas.

O Modelo

Este modelo é um exemplo simples que ilustra um controlo por tempo utilizando a biblioteca Tweenjs para fazer interpolações (tweens) e também um controlo por passos.

1. O modelo é inicializado na função init_model — esta função define um objeto com os parâmetros necessários para a animação, mais alguns usados na visualização e acrescenta alguns métodos a esse objeto para tornar a programação da animação mais sistemática e ergonómica.
2. O modelo é atualizado em cada passo da animação através do método update.
3. Esta animação tem um controlo por tempo (tweens) para a posição do leader e também um controlo por passos para o follower.

Estado Inicial

Pretende-se que o movimento do leader percorra os quatro cantos do espaço e que o follower o persiga, limitado a uma velocidade máxima.

• As posições, tanto do leader como do follower são representadas pelos atributos pos: {x:, y:} que usam coordenadas cartesianas.
• Também são comuns outras propriedades gráficas, como o tamanho (size) e cor (color).
• O leader não precisa de velocidade porque a sua posição é diretamente controlada por tweens.
• O follower precisa de velocidade porque o seu movimento é constantemente orientado para a posição do leader. Além disso, este movimento deve estar limitado a uma rapidez máxima, max_speed.
• Também o modelo tem atributos gráficos para definir o tamanho da cena (width, height) e a cor de fundo (background).
• Finalmente, age é a «idade» do modelo, isto é, o seu número de passos (atualizações).

function init_model() {
  const model = {
    age: 0,
    leader: {
      pos: { x: 0, y: 0 },
      size: 16,
      color: "crimson",
    },
    follower: {
      pos: { x: 246, y: 246 },
      vel: { x: 0, y: 0 },
      max_speed: 1000,
      size: 8,
      color: "steelblue",
    },
    background: "khaki",
    width: 256,
    height: 256,
  };
  
  // Further instructions

  return model;
}

Controlo por Tempo

O movimento do leader é controlado por tempo; para esse efeito usa-se a biblioteca tween.js.

O leader deve deslocar-se pelos quatro cantos da cena, como neste exemplo.

function init_model() {
  const model = { ... };

  const duration_ms = 1000;
  const easing = Easing.Cubic.InOut;
  const right = new Tween(model.leader.pos)
    .to(
      {
        x: model.width - model.leader.size,
        y: 0,
      },
      duration_ms,
    )
    .easing(easing);
  const down = new Tween(model.leader.pos)
    .to(
      {
        x: model.width - model.leader.size,
        y: model.height - model.leader.size,
      },
      duration_ms,
    )
    .easing(easing);
  const left = new Tween(model.leader.pos)
    .to({ x: 0, y: model.height - model.leader.size }, duration_ms)
    .easing(easing);
  const up = new Tween(model.leader.pos)
    .to({ x: 0, y: 0 }, duration_ms)
    .easing(easing);

  right.chain(down);
  down.chain(left);
  left.chain(up);
  up.chain(right);
  right.start();

  const group = new Group();
  group.add(right, down, left, up);
  model.leader.tween = group;

  // Further instructions

  return model;
}

• O grupo de tweens é adicionado a model no atributo model.leader.tween.
• Posteriormente, durante a atualização, esse grupo será atualizado de forma a controlar a posição do leader.

Tempos e Atualização

Os restantes atributos do modelo representam (1) momentos «importantes» e (2) o método de atualização.

function init_model() {
  const model = { ...
  };

  // Previous instructions

  model.start = performance.now();
  model.last_ts = model.start;

  model.update = update;

  return model;
}

O atributo model.last_ts é atualizado em cada passo da animação e regista o momento em que esse passo foi executado. Esta informação é importante para determinar o tempo decorrido desde o passo anterior.

Atualização do Modelo

A atualização do modelo é implementada no método update e segue uma determinada sequência.

1. Atualização dos tempos — deste o passo anterior; número de passos, etc.
2. Atualização dos tweens para controlo da posição do leader.
3. Velocidade e posição do follower — a nova posição do leader determina um novo rumo para o follower; esse cálculo é mais simples usando coordenadas polares.

Atualização dos Tempos

function update(ts) {
  this.age += 1;
  const dt = 0.001 * (ts - this.last_ts);
  this.last_ts = ts;

  // Further instructions 
}

O argumento ts é o timestamp (carimbo temporal) e é o instante (em milisegundos) de evocação do método update.

• As primeiras instruções tratam do progresso do tempo:
• this.age += 1; incrementa a «idade» do modelo;
• As restantes duas instruções determinam:
  • O tempo decorrido deste o passo anterior (dt).
  • Atualizam o registo do momento do passo this.last_ts = ts.

Atualização dos Tweens

A posição do leader é controlada pelo atributo leader.tween.

• Este atributo é um grupo de tweens definido na inicialização do modelo.
• Um grupo de tweens permite a atualização simultânea de todos os tweens nesse grupo.

function update(ts) {
  // Previous instructions

  this.leader.tween.update(ts);

  // Further instructions
}

Com os tweens bem definidos na inicialização do modelo basta esta instrução para atualizar a posição do leader.

Velocidade e Posição do Seguidor

O follower (seguidor) desloca-se na direção do leader mas tem a velocidade limitada a um valor máximo (model.follower.max_speed).

Este passo é idêntico ao exemplo seguidor interativo.

function update(ts) {
  // Previous instructions

  this.leader.tween.update(ts);

  // FOLLOWER
  //
  // Heading
  const follower_heading_cart = dir(this.follower.pos, this.leader.pos);
  const follower_heading_pol = cart2polar(follower_heading_cart);
  //
  // Max speed
  follower_heading_pol.d = Math.min(
    this.follower.max_speed,
    dist(this.follower.pos, this.leader.pos),
  );
  //
  // Cartesian vel
  this.follower.vel = polar2cart(follower_heading_pol);
  //
  // Position update
  this.follower.pos.x += this.follower.vel.x * dt;
  this.follower.pos.y += this.follower.vel.y * dt;
}

A Biblioteca do Modelo

Toda a funcionalidade que diz respeito ao modelo dve ficar «isolada» numa biblioteca, importando e exportando apenas o que for necessário.

Conteúdo do ficheiro model_grsystems.js

import { Tween, Easing, Group } from "tween";
export { init_model };

function cart2polar(p) { ... }
function polar2cart(p) { ... }
function dir(p, q) { ... }
function dist(p, q) { ... }

function init_model() {
  ... 
  return model;
}

function update(ts) {
  ... 
}

• A primeira instrução importa a biblioteca tween porque são necessários tweens para o controlo da posição do leader.
• A instrução export { init_model }; declara que a única função definida aqui que pode ser usada «fora» é init_model.
• As restantes linhas definem as várias funções e métodos de apoio a init_model.

A função init_model devolve o objeto model; todos os atributos e métodos de model definidos nessa função são acessíveis «fora» da biblioteca.

A Visualização

A visualização do modelo consiste na construção (render) de uma imagem em cada passo da animação, para cada um dos quatro sistemas gráficos C2D, SVG, 3JS e X3D.

Visualização C2D

No exemplo Seguidor Interativo já se definiu suporte para a visualização em C2D, que também funciona para este modelo.

Para esta visualização falta «arrumar» a inicialização numa função (new_context_c2d) e agrupar «tudo» numa biblioteca (render_c2d.js):

export { new_context_c2d };

function render_c2d(m) { ... }
function render_char(c) { ... }

function new_context_c2d(target_c2d, model) {
  const context = document.getElementById(target_c2d).getContext("2d");
  context.render = render_c2d;
  context.render_char = render_char;
  context.canvas.width = model.width;
  context.canvas.height = model.height;

  return context;
}

Esta biblioteca exporta apenas a função new_context_c2d:

• O argumento target_c2d é o identificador do elemento <canvas> onde esta visualização vai ser construída.
• O argumento model serve para dimensionar esse <canvas>.
• O objeto devolvido, context, é um CanvasRenderingContext2D a que foram acrescentados os métodos render e render_char.

Visualização SVG

A visualização usando o sistema SVG depende da existência de certos elementos SVG no documento HTML e agrupa esses elementos com funções para os inicializar e atualizar.

Elementos SVG

<svg id="svg:container" width="256px" height="256px">
    <rect
        id="svg:bg"
        x="0"
        y="0"
        width="256"
        height="256"
        fill="khaki"
    />
    <rect
        id="svg:leader"
        x="60"
        y="60"
        width="15"
        height="15"
        fill="crimson"
    />
    <rect
        id="svg:follower"
        x="200"
        y="200"
        width="10"
        height="10"
        fill="steelblue"
    />
</svg>

No fragmento HTML acima estão identificados:

• O elemento svg tem id="svg:container".
• Os elementos rect têm:
  • id="svg:bg" para o fundo.
  • id="svg:leader" para o leader.
  • id="svg:follower" para o follower.

Biblioteca para um «Contexto» SVG.

O «contexto» SVG tem informação sobre quais são os elementos a atualizar (o leader e o follower) e métodos para atualizar os respetivos atributos.

Para esta animação particular as identificações do leader e do follower, agrupados num único objeto, ficam:

const objects_svg = {
  leader: "svg:leader",
  follower: "svg:follower"
}

Este objeto tem a informação necessária para construir e atualizar um «contexto» SVG. Toda essa funcionalidade deve ficar agrupada numa biblioteca (render_svg.js):

export { new_context_svg };

function render_svg(m) {
  this.leader.setAttribute("x", m.leader.pos.x);
  this.leader.setAttribute("y", m.leader.pos.y);
  this.follower.setAttribute("x", m.follower.pos.x);
  this.follower.setAttribute("y", m.follower.pos.y);
}

function new_context_svg(objects_svg) {
  return {
    leader: document.getElementById(objects_svg.leader),
    follower: document.getElementById(objects_svg.follower),
    render: render_svg,
  };
}

Esta biblioteca exporta apenas a função new_context_svg:

• O argumento objects_svg tem a estrutura já ilustrada, com os id dos elementos a animar.
• O objeto devolvido tem:
  • Os elementos leader e follower identificados.
  • O método render, que é executado pela função render_svg.
• A função render_svg:
  • Tem argumento m, um modelo («compatível»).
  • Usa as posições do leader e do follower do modelo (m.leader.pos e m.follower.pos) para atualizar as posições (os atributos "x" e "y") do leader e do follower do contexto (this).

Visualização X3D

A visualização para o sistema X3D é muito semelhante à visualização para SVG dado que estes dois sistemas definem a visualização com elementos integrados no documento (veja Document Object Model (DOM)).

Elementos X3D

Os objetos gráficos no X3D são posicionados (e rodados, dimensionados, etc.) usando elementos Transform. Portanto no X3D os objetos leader e follower são, de facto, Transform:

<X3D width="256px" height="256px">
    <Scene>
        <Background skyColor=".98 .98 .92"></Background>
        <Transform id="x3d:leader" translation="-6 -6 0">
            <Shape>
                <Appearance>
                    <Material id="x3d:leader.material" diffuseColor="crimson"> </Material>
                </Appearance>
                <Box size="0.6 0.6 0.6"></Box>
            </Shape>
        </Transform>
        <Transform id="x3d:follower" translation="0 0 0">
            <Shape>
                <Appearance>
                    <Material diffuseColor="steelblue"> </Material>
                </Appearance>
                <Box size="0.2 0.2 0.2"></Box>
            </Shape>
        </Transform>
    </Scene>
</X3D>

Neste fragmento estão identificados os elementos Transform:

• id="x3d:leader" para o leader.
• id="x3d:follower" para o follower.

Limites Geométricos do Modelo e Sistemas 3D

As posições e as dimensões dos objetos do modelo estão em escalas significativamente diferentes das escalas típicas num sistema 3D.

O modelo existe num espaço 2D, com coordenadas x,y e limites 256x256. Num sistema gráfico 3D é necessária mais uma coordenada (z) e tipicamente os limites são menores (por exemplo, 10 x 10 x 10).

Por isso:

• As dimensões das geometrias acima são reduzidas:
  • <Box size="0.6 0.6 0.6"></Box> para o leader.
  • <Box size="0.2 0.2 0.2"></Box> para o follower.
• As funções que atualizarem as visualizações 3D terão de fazer um ajuste adequado às posições que o modelo reporta.

Biblioteca para um «Contexto» X3D.

O «contexto» X3D tem informação sobre quais são os elementos a atualizar (o leader e o follower) e métodos para atualizar os respetivos atributos.

Para esta animação particular as identificações do leader e do follower, agrupados num único objeto, ficam:

const objects_x3d = {
  leader: "x3d:leader",
  follower: "x3d:follower"
};

Este objeto tem a informação necessária para construir e atualizar um «contexto» X3D. Toda essa funcionalidade deve ficar agrupada numa biblioteca (render_x3d.js):

export { new_context_x3d };

function render_x3d(m) {
  const leader_x = (m.leader.pos.x / m.width - 0.5) * 5;
  const leader_y = (m.leader.pos.y / m.height - 0.5) * 5;
  this.leader.setAttribute("translation", `${leader_x} ${leader_y} 0.0`);
  const follower_x = (m.follower.pos.x / m.width - 0.5) * 5;
  const follower_y = (m.follower.pos.y / m.height - 0.5) * 5;
  this.follower.setAttribute("translation", `${follower_x} ${follower_y} 0.0`);
}

function new_context_x3d(objects_x3d) {
  return {
    leader: document.getElementById(objects_x3d.leader),
    follower: document.getElementById(objects_x3d.follower),
    render: render_x3d,
  };
}

Esta biblioteca exporta apenas a função new_context_x3d:

• O argumento objects_x3d tem a estrutura já ilustrada, com os id dos elementos a animar.
• O objeto devolvido tem:
  • Os elementos leader e follower identificados.
  • O método render, que é executado pela função render_x3d.
• A função render_x3d:
  • Tem argumento m, um modelo («compatível»).
  • Usa as posições do leader e do follower do modelo (m.leader.pos e m.follower.pos) para atualizar as posições (os atributos "translation") do leader e do follower do contexto (this).
• Nesta atualização as coordenadas «do modelo» são convertidas para coordenadas típicas em sistemas 3D:
  • Os valores x do modelo variam entre 0 e m.width e são convertidos para valores entre -2.5 e 2.5.
  • Analogamente, os valores y do modelo, que variam entre 0 e model.height, são convertidos para valores entre -2.5 e 2.5.

Visualização 3JS

O sistema 3JS é semelhante ao sistema X3D e SVG porque os objetos gráficos são «pré-construídos» mas, como o C2D, o modelo gráfico é definido por instruções e estruturas de dados.

O esquema usado para os outros sistemas gráficos é o seguinte:

• Define-se uma biblioteca render_XYZ.js.
• Essa biblioteca exporta uma função new_context_XYZ que:
  • Tem como argumentos a informação necessária inicialização do «contexto», como a identificação dos elementos dom ou o próprio modelo.
  • Devolve um objeto, um «contexto», com um método render adequado à visualização do modelo.

Com base nos modelos disponíveis, a biblioteca render_3js.js fica:

import * as THREE from "three";
import { OrbitControls } from "three/addons/controls/OrbitControls.js";

export { new_context_3js };

function new_context_3js(container_id, model) {
  // New Context for 3JS 
}

Esta biblioteca exporta apenas a função new_context_3js, detalhada mais abaixo.

• O argumento container_id é o identificador de um elemento (no documento) onde esta visualização vai ser construída.
• O argumento model serve para dimensionar esse elemento.

Um «Contexto» para 3JS

A inicialização do «contexto» para o sistema 3JS segue os passos que estão descritos, por exemplo, aqui:

function new_context_3js(container_id, model) {
  const container = document.getElementById(container_id);
  container.width = model.width;
  container.height = model.height;

  const renderer = new THREE.WebGLRenderer({ alpha: true });
  renderer.setPixelRatio(window.devicePixelRatio);
  renderer.setSize(container.width, container.height);
  renderer.setClearColor("#FAFAEB", 1.0);
  container.appendChild(renderer.domElement);

  const camera = new THREE.PerspectiveCamera(
    35, // abertura
    container.width / container.height, // proporção largura/altura
    0.1, // corte perto
    10000, // corte longe
  );
  camera.position.set(-2.5, 0, 20);

  const controls = new OrbitControls(camera, renderer.domElement);

  const scene = new THREE.Scene();
  camera.lookAt(scene.position);
  
  const light = new THREE.AmbientLight("white");
  light.intensity = 2.0;
  scene.add(light);

  // Further instructions
}

Neste fragmento está definido:

1. Uma referência para o elemento HTML que vai receber a visualização: container.
2. Um objeto para construir a visualização da cena: renderer.
3. Uma câmara para definir a visualização da cena: camera.
4. Um objeto para controlar a câmara: controls.
5. Uma cena para conter os objetos gráficos: scene.
6. Iluminação para iluminar a cena: light.

Falta adicionar objetos gráficos para o leader e para o follower:

function new_context_3js(container_id, model) {
  const container = ...;
  const renderer = ...;
  const camera = ...;
  const controls = ...;
  const scene = ...;
  const light = ...;

  //
  // LEADER
  const leader_geo = new THREE.BoxGeometry(0.6, 0.6, 0.6);
  const leader_mat = new THREE.MeshLambertMaterial({
    color: model.leader.color,
  });
  const leader = new THREE.Mesh(leader_geo, leader_mat);
  scene.add(leader);

  // FOLLOWER
  const follower_geo = new THREE.BoxGeometry(0.2, 0.2, 0.2);
  const follower_mat = new THREE.MeshLambertMaterial({
    color: model.follower.color,
  });
  const follower = new THREE.Mesh(follower_geo, follower_mat);
  scene.add(follower);

  // Further instructions
}

Todos os elementos da visualização estão definidos. Falta definir o método de atualização (render) e devolver o «contexto»:

function new_context_3js(container_id, model) {
  const container = ...;
  const renderer = ...;
  const camera = ...;
  const controls = ...;
  const scene = ...;
  const light = ...;

  //
  // LEADER
  const leader = ...;

  // FOLLOWER
  const follower = ...;

  //
  // RENDER
  function render(m) {
    controls.update(); // Atualizar os controlos
    const leader_x = (m.leader.pos.x / m.width - 0.5) * 5;
    const leader_y = (m.leader.pos.y / m.height - 0.5) * 5;
    leader.position.set(leader_x, leader_y, 0);

    const follower_x = (m.follower.pos.x / m.width - 0.5) * 5;
    const follower_y = (m.follower.pos.y / m.height - 0.5) * 5;
    follower.position.set(follower_x, follower_y, 0);
    renderer.render(scene, camera); // Construir a cena atualizada
  }

  return {
    render: render,
  };
}

• O objeto devolvido é {render: render} que usa a função render para atualizar as posições do leader e do follower e a visualização da cena.
• Tal como na visualização do X3D, as coordenadas do modelo são convertidas (da mesma forma) para um referencial mais típico em sistemas 3D.

Este exemplo funciona porque a função function render(m) { ... } «capta» todo o contexto em que é definida.

Isto é, render(m) mantém «vivos» os objetos no contexto em que é definida e que refere diretamente e também os objetos que refere indiretamente. Por exemplo:

• Referências diretas do contexto: controls, leader, follower, renderer, scene, camera.
• Referências indiretas: container, light, e os vários objetos auxiliares (e.g. leader_geo).

O Ciclo de Animação

O ciclo de animação inclui a atualização seguida da visualização do modelo nos quatro sistemas gráficos e é definido pela função step. Este nível mais elevado da animação pode ficar na sua própria biblioteca, onde são compostos e arranjados (quase) todos os elementos principais.

• São importadas as bibliotecas de adaptação aos sistemas gráficos e também a biblioteca do modelo.
• Os argumentos da função main() identificam os elementos html controlados pela animação.
• O modelo, e os «contextos» são inicializados.
• É definido o passo do ciclo de animação.
• É ativado o ciclo de animação.

Conteúdo do ficheiro grsystems.js:

import { new_context_c2d } from "render_c2d";
import { new_context_svg } from "render_svg";
import { new_context_3js } from "render_3js";
import { new_context_x3d } from "render_x3d";
import { init_model } from "model";

export { main as default };

function main(
  target_c2d,
  target_3js,
  target_terminal,
  objects_svg,
  objects_x3d,
) {
  const terminal = document.getElementById(target_terminal);
  const write = (text) => {
    terminal.innerText = text;
  };

  const model = init_model();

  const context_c2d = new_context_c2d(target_c2d, model);
  const context_svg = new_context_svg(objects_svg);
  const context_x3d = new_context_x3d(objects_x3d);
  const context_3js = new_context_3js(target_3js, model);

  const step = function (ts) {
    model.update(ts);
    write(`AGE: ${model.age}`);
    context_c2d.render(model);
    context_svg.render(model);
    context_x3d.render(model);
    context_3js.render(model);

    requestAnimationFrame(step);
  };

  requestAnimationFrame(step);
}

1. terminal é o elemento html que vai ser a «consola», onde é mostrada informação textual; A função write permite escrever para essa «consola».
2. model é inicializado pela função init_model.
3. São criados quatro contextos, um para cada sistema: context_c2d, context_svg,context_x3d,context_3js.
4. A função step define o passo no ciclo de animação:
5. O modelo é atualizado;
6. É mostrada a idade do modelo na consola;
7. O modelo é simultaneamente visualizado nos quatro «contextos».
8. É colocado um pedido para o browser executar step na próxima atualização desta página.
9. É colocado o primeiro pedido para o browser executar step na próxima atualização desta página.

A Parte HTML

A animação existe num documento HTML que tem de incorporar os vários containers para as visualizações, assim como definir as importações necessárias.

Suporte para o X3D:

<script
    type="application/javascript"
    src="./lib/x3dom/x3dom-full.js"
></script>
<link
    rel="stylesheet"
    type="text/css"
    href="./lib/x3dom/x3dom.css"
/>

Importação de bibliotecas JavaScript. Inclui:

• tweens com o tween.js.
• 3JS e respetivos addons (para o controlo orbital da câmara).
• As bibliotecas descritas aqui: o modelo (model), os «contextos» (render_XYZ) e o controlo da animação (grsystems).

<script type="importmap">
    {
        "imports": {
            "tween": "./lib/tweenjs/tween.esm.js",
            "three": "./lib/threejs/build/three.module.js",
            "three/addons/": "./lib/threejs/addons/jsm/",
            "grsystems": "./grsystems.js",
            "model": "./model_grsystems.js",
            "render_c2d": "./render_c2d.js",
            "render_svg": "./render_svg.js",
            "render_3js": "./render_3js.js",
            "render_x3d": "./render_x3d.js"
        }
    }
</script>

Grelha com as visualizações:

<div style="display:grid;grid-template-columns:256px 256px;margin:0 auto;width: fit-content">
    <div id="terminal" style="font-family: monospace;padding:0.5em;background:black;color:seagreen;grid-column:1/ span 2">TERMINAL</div>
    <canvas id="c2d:canvas"></canvas>
    <div id="3js:container"></div>
    <X3D width="256px" height="256px">
        ...
    </X3D>
    <svg id="svg:container" width="256px" height="256px">
        ...
    </svg>
</div>

Ativação da animação:

<script type="module">
    import main from "grsystems";
    const objects_svg = {
      leader: "svg:leader",
      follower: "svg:follower"
    };
    const objects_x3d = {
      leader: "x3d:leader",
      follower: "x3d:follower"
    };
    main("c2d:canvas", "3js:container", "terminal", objects_svg, objects_x3d);
</script>

O Que Falta (Exercícios)

Uma Imagem Estereoscópica

• Torne a animação mais sofisticada, seguindo estas sugestões.
• Esta animação não tem eventos externos. Procure na documentação adequada como controlar o movimento do leader usando o rato.
• Adicione a possibilidade de pausar a animação: em modo de pausa o modelo apenas atualiza um conjunto reduzido de parâmetros (e.g. age e last_ts).
• Considere uma variante deste exercício em que, em vez de quarto sistemas gráficos, usa duas visualizações 3JS do mesmo modelo que diferem apenas ligeiramente na posição da câmara. Isto é, faça uma visualização estereoscópica da animação.

Referenciais e Hierarquias

Um modelo hierárquico com estados.

TERMINAL

Este exemplo ilustra uma animação com várias caraterísticas:

1. O modelo é uma hierarquia de objetos e sub-objetos, suportada por transformações entre os espaços (referenciais) adequados.
2. O modelo tem estados que controlam as «fases» da animação.
3. Implementa um «mini sistema gráfico» declarativo (como o SVG ou o X3D) sobre o C2D.

Hierarquias de Objetos gráficos

A cena deve organizar os objetos gráficos num grafo que representa a estrutura do modelo.

Neste exemplo temos o seguinte grafo — os nós retangulares representam formas e os nós ovais representam «grupos».

---
config:
  theme: neutral
---
graph TD;
model([model]) ==> truck([truck])
model -.-> bin

truck ==> bin([bin])
truck ==> chassis
truck ==> cabin
truck ==> glass
truck ==> wheel1
truck ==> wheel2
truck ==> wheel3

bin ==> box

model ===> floor
model ===> background

Cada grupo define um «espaço» que organiza os seus descendentes. Para tal, no âmbito deste exemplo, definimos um objeto gráfico como um objeto javascript com os seguintes atributos:

{
  tr: {x: ..., y: ..., alpha: ..., sx: ..., sy: ...},
  shape: ...,
  style: { fill: ..., stroke: ..., lineWidth: ... },
  children: [ ... ]
}

em que:

• tr define uma transformação que se aplica a esse objeto e a todos os seus descendentes (children).
• shape define a geometria do objeto.
• style define as propriedades visuais do objeto.
• children define os descendentes (sub-objetos subordinados) que herdam a transformação.

Além disso:

• Cada atributo e sub-atributo é opcional.
• As arestas sólidas representam descendentes. Por exemplo, glass é descendente de truck, que é descendente de model.
• Há uma aresta pontilhada, de model para bin, que representa uma referência. Isto é, bin não é sub-elemento de model mas é referido por um atributo: model.bin.

Esta convenção equilibra «capacidade expressiva» com «simplicidade».

---

Por exemplo, o objeto («grupo») bin fica definido por:

{
  tr: { x: -0.85, y: -0.7, alpha: 0 * Math.PI },
  children: [
    {
      tr: { x: 0.5, y: 0.5, sx: 0.5, sy: 0.5 },
      shape: "M 0 0 m 1 0.5 l -1.5 0 l -0.5 -0.5 l 0 -0.5 l 2 0 l 0 1 Z",
      style: {
        fill: "maroon",
        stroke: "firebrick",
        lineWidth: 0.2,
      },
    },
  ],
}

Este objeto não tem nem forma (shape) nem propriedades visuais (style). No entanto, define uma transformação (tr: { x: -0.85, y: -0.7, alpha: 0 * Math.PI }) e tem um descendente (box no diagrama acima). Neste descendente:

1. A forma (shape) é definida por um caminho que usa a sintaxe dos caminhos SVG (o atributo d dos elementos path)
2. As propriedades visuais (style) definem como é pintado e traçado.
3. A transformação (tr) posiciona-o (x: ..., y: ...) e dimensiona-o (sx: ..., sy: ...) no referencial do seu parente.

Um Sistema Gráfico Dedicado

A visualização de cenas (e modelos) com aquele tipo de objetos gráficos assenta numa extensão do sistema C2D com métodos e funções adequadas.

Transformação

Definir o espaço/referencial do objeto gráfico no objeto «parente».

A transformação, se definida, aplica-se logo no início da visualização porque afeta as instruções de desenho e, também, os descendentes.

/**
A Graphical Object is an object with attributes:
- `tr`: a transformation: `x,y` translation; `alpha` rotation; `sx,sy` scale;
- `children`: sub-objects;
- `shape`: A "path" program;
- `style`: visual properties:  `stroke`; `fill`; `lineWidth`;
*/
function render(grobj) {
  if (grobj.tr) {
    const x = grobj.tr.x || 0.0;
    const y = grobj.tr.y || 0.0;
    const alpha = grobj.tr.alpha || 0.0;
    const sx = grobj.tr.sx || 1.0;
    const sy = grobj.tr.sy || 1.0;
    this.save();
    this.translate(x, y);
    this.rotate(alpha);
    this.scale(sx, sy);
  }

  // Further instructions
  
  if (grobj.tr) this.restore();
}

A última instrução

  if (grobj.tr) this.restore();

garante que os efeitos da (eventual) transformação aplicada no início são repostos no estado anterior.

Descendentes

Aplicar recursivamente a visualização aos descendentes.

A visualização dos descendentes (se definidos) usa exatamente a mesma função de visualização:

function render(grobj) {
  if (grobj.tr) { ... }

  if (grobj.children)
    grobj.children.forEach((child) => this.render(child));

  // Further instructions
  
  if (grobj.tr) this.restore();
}

Aqui está-se a utilizar o método Array.forEach porque o código fica mais legível.

Visualização

Usar o sistema C2D para visualizar o objeto gráfico.

Se o objeto gráfico tiver definidas uma forma e propriedades visuais, é necessário:

1. Definir a forma no sistema C2D.
2. Aplicar as propriedades visuais que estejam definidas; «traçar» o contorno; «pintar» o interior.

function render(grobj) {
  if (grobj.tr) { ... }

  if (grobj.children) { ... }

  if (grobj.shape && grobj.style) {
    const shape = new Path2D(grobj.shape);  // Geometry
    if (grobj.style.stroke) {               // Stroke?
      const prev_lineWidth = this.lineWidth;
      this.lineWidth = grobj.style.lineWidth || this.lineWidth;
      this.strokeStyle = grobj.style.stroke;
      this.stroke(shape);
      this.lineWidth = prev_lineWidth;
    }
    if (grobj.style.fill) {                 // Fill?
      this.fillStyle = grobj.style.fill;
      this.fill(shape);
    }
  }

  if (grobj.tr) this.restore();
}

As instruções

const prev_lineWidth = this.lineWidth;
...
this.lineWidth = prev_lineWidth;

são necessárias porque a propriedade C2D.lineWidth não fica registada com o método .save(). Desta forma (1) guardam o valor prévio desse atributo e depois (2) repõem o valor guardado.

Objetos Primitivos

Funções de suporte para algumas formas e transformações simples.

Um quadrado centrado na origem e de lado 2:

function urect() {
  return "M 0 0 m -1 -1 l 2 0 l 0 2 l -2 0 l 0 -2 Z";
}

Um círculo centrado na origem e de raio 1:

function ucirc() {
  return "M 0 0 m 1 0 a 1 1 0 1 0 -2 0 a 1 1 0 1 0 2 0";
}

A transformação identidade:

function tid() {
  return { x: 0.0, y: 0.0, sx: 1.0, sy: 1.0, alpha: 0.0 };
}

Inicialização

Criar um contexto gráfico adequado.

A inicialização do contexto adiciona o método render (explicado acima) a um CanvasRenderingContext2D. Adicionalmente, ajusta a dimensão do canvas respetivo e ajusta o referencial com:

Orientação «Matemática»

de forma que

Canto	Coordenadas
Superior Esquerdo	$(-1, +1)$
Inferior Esquerdo	$(-1, -1)$
Superior Direito	$(+1, +1)$
Inferior Direito	$(+1, -1)$

Adicionalmente, a inicialização do contexto gráfico também acrescenta o método print para mostrar mensagens de texto num elemento indicado.

function new_context(container_id, terminal_id, width, height) {
  const context = document.getElementById(container_id).getContext("2d");

  const terminal = document.getElementById(terminal_id);
  context.print = (text) => (terminal.innerHTML = text);

  context.render = render;

  context.canvas.width = width;
  context.canvas.height = height;
  context.save();

  context.lineWidth = 1.0 / Math.max(context.canvas.width, context.canvas.height, 1);

  context.translate(0.5 * context.canvas.width, 0.5 * context.canvas.height);
  context.scale(0.5 * context.canvas.width, -0.5 * context.canvas.height);

  return context;
}

A instrução

  context.lineWidth = 1.0 / Math.max(context.canvas.width, context.canvas.height, 1);

ajusta a espessura do traço a 1% da maior dimensão da tela.

As duas instruções

  context.translate(0.5 * context.canvas.width, 0.5 * context.canvas.height);
  context.scale(0.5 * context.canvas.width, -0.5 * context.canvas.height);

ativam a orientação «Matemática» do referencial e definem as coordenadas dos cantos como mostrado acima.

A Biblioteca Gráfica

Toda a funcionalidade do contexto gráfico fica agrupada numa biblioteca (minigrsys.js)

export { urect, ucirc, tid, new_context };

function urect() { ... }
function ucirc() { ... }
function tid() { ... }
function new_context(container_id, terminal_id, width, height) { ... }
function render(grobj) { ... }

Modelo

O modelo deve conter informação sobre o grafo de cena, a «fase» da animação, o estado de «pausa» e um método para a atualização.

• O grafo de cena tem os elementos gráficos, cada um com transformações; forma; propriedades visuais; descendentes.
• As «fases» da animação são: andar para a direita; «descarregar» a carga; voltar à «base».
• Se a animação está em «pausa» os atributos não são atualizados.
• O método update faz a atualização passo-a-passo do modelo.
• É ainda necessário integrar informação «temporal»: o ciclo (age); e o carimbo temporal da atualização anterior (last_ts).

Representação da informação «temporal» e das fases da animação:

function init_model() {
  const model = {
    age: 0,
    paused: false,
    phase: 0,
    phase_age: 0,
  };
  
  // Further instructions
  
  model.last_ts = performance.now();
  return model;
}

O atributo age é o contador de ciclos de animação que o modelo «viveu» e paused controla se o modelo está, ou não em modo «pausa».

Mais à frente, na explicação do método update, vai ser mostrado como a «pausa» afeta a evolução do modelo mas por enquanto interessa associar-lhe um evento de teclado:

function init_model() {
  const model = { ... };

  document.addEventListener("keydown", (e) => {
    if (e.key === "p") {
      model.paused = !model.paused;
    }
  });
  
  // Further instructions
  
  model.last_ts = performance.now();
  return model;
}

Desta forma cada vez que é premida a tecla p o valor Booleano de model.paused é invertido: o modelo passa de paused para running e vice-versa.

Descendentes

Além de definir os descendentes de um modelo é também conveniente identificar alguns desses descendentes com «acesso direto».

function init_model() {
  const model = { ... };

  document.addEventListener("keydown", ... );
  
  model.add_child = add_child;
  
  // Further instructions
  
  model.last_ts = performance.now();
  return model;
}

function add_child(name, grobj) {
  if (!this.children) this.children = [];
  this.children.push(grobj);
  this[name] = grobj;
}

O método add_child pode ser adicionado a qualquer objeto gráfico; acrescenta um descendente (grobj) a esse objeto e identifica-o pelo atributo name.

• Sem este método continuaria a ser possível aceder a cada descendente, pelo seu índice na lista/atributo .children — uma forma pouco ágil.

O fundo (background) e o chão (floor) são colocados no modelo desta forma:

function init_model() {
  const model = { ... };

  document.addEventListener("keydown", ... );
  
  model.add_child = add_child;
  
  model.add_child("background", {
    shape: urect(),
    tr: { x: 0.0, y: 0.0, sx: 1.0, sy: 1.0, },
    style: { fill: "lightskyblue" },
  });

  model.add_child("floor", {
    shape: urect(),
    tr: { x: 0.0, y: -0.9, sx: 1.0, sy: 0.1, },
    style: { fill: "slategray" },
  });
  
  model.last_ts = performance.now();
  return model;
}

Desta forma o modelo passou a ter mais dois atributos: background e floor que referem diretamente o fundo e o chão respetivamente.

---

Note-se que o fundo é um retângulo unitário centrado ({x: 0.0, y: 0.0}) e dimensionado ({sx: 1.0, sy: 1.0}) de forma a cobrir toda a área da tela — neste caso esta transformação não é necessária porque coincide com a posição e dimensão de urect.

---

A inicialização do modelo ainda não está completa: falta adicionar o camião e o método de atualização.

Camião

Este é o «ator» principal da animação: desloca-se para a esquerda e para a direita e tem vários descendentes. Desses, o contentor também tem a sua animação, rodando quando o camião para.

Dada a (relativa) complexidade do camião, assim como do contentor, estes objetos gráficos são definidos em funções dedicadas.

O contentor fica definido em:

function bin() {
  return {
    tr: { x: -0.85, y: -0.5, alpha: 0 * Math.PI },
    children: [
      { // The rotation axis
        tr: { sx: 0.05, sy: 0.05 }, 
        shape: ucirc(), 
        style: { fill: "black" } },
      { // The bin "sub-object"
        tr: { x: 0.5, y: 0.3, sx: 0.5, sy: 0.5 },
        shape: "M 0 0 m 1 0.5 l -1.5 0 l -0.5 -0.5 l 0 -0.5 l 2 0 l 0 1 Z",
        style: {
          fill: "maroon",
          stroke: "firebrick",
          lineWidth: 0.2,
        },
      },
    ],
  };
}

O aspeto mais interessante deste objeto gráfico tem a ver com a forma como é rodado: Não em torno do centro da geometria, mas do eixo assinalado pelo (semi) ponto preto.

Para se obter esta rotação «fora do centro» é preciso «re-centrar» o objeto gráfico para o eixo pretendido; e, além de ajustar o tamanho, é precisamente esse o papel da transformação «local»:

function bin() {
  return {
    ...
      { // The bin "sub-object"
        tr: { x: 0.5, y: 0.3, sx: 0.5, sy: 0.5 },
        ...
      },
    ...  
  };
}

O camião tem o contentor, e outro objetos, como descendentes:

function truck() {
  const truck_obj = {
    tr: tid(),
    children: [
      { // Chassis
        shape: urect(),
        tr: { x: -0.05, y: -0.6, sx: 0.8, sy: 0.05 },
        style: { fill: "darkolivegreen" },
      },
      { // Cabin
        shape: "M 0 0 l 1 0 l 0 -1 l -2 0 l 0 2 l 1 0 l 0 -1 Z",
        style: { fill: "darkgreen" },
        tr: { x: 0.5, y: -0.3, sx: 0.25, sy: 0.25 },
      },
      { // Glass
        shape: "M 0 0 l 1 0  a 1 1 0 0 1 -1 1 l 0 -1 Z",
        style: { fill: "lightcyan" },
        tr: { x: 0.5, y: -0.3, sx: 0.25, sy: 0.25 },
      },
      wheel(-0.65, -0.7), // 3 Wheels
      wheel(-0.35, -0.7), // each defined by the
      wheel(0.5, -0.7),   // same function...
    ],
  };
  // The bin
  truck_obj.add_child = add_child;
  truck_obj.add_child("bin", bin());

  return truck_obj;
}

As rodas fazem parte do camião. Como objeto gráfico, são simples, mas são três. Para não repetir código, definem-se numa função:

function wheel(x, y) {
  return {
    shape: ucirc(),
    tr: { x: x, y: y, sx: 0.05, sy: 0.05 },
    style: {
      fill: "gray",
      stroke: "black",
      lineWidth: 2.0,
    },
  };
}

A inicialização do modelo fica completa com o camião e com uma referência ao contentor:

function init_model() {
  const model = { ... };

  document.addEventListener("keydown", ... );
  
  model.add_child = add_child;
  
  model.add_child("background", ... );
  model.add_child("floor", ... );
  
  model.add_child("truck", truck());
  // Adjust the position
  model.truck.tr = { x: -0.8, y: -0.4, sx: 0.25, sy: 0.5 };
  // Get a reference to the bin.
  model["bin"] = model.truck.bin;

  model.update = update;
  
  model.last_ts = performance.now();
  return model;
}

e falta apenas definir a atualização — o método update.

Atualização

Esta animação tem fases distintas, onde acontece o movimento do camião e do contentor.

O movimento do camião segue uma sequência fixa de fases:

1. Vira-se para a «direita» e desloca-se «em frente».
2. Levanta o contentor.
3. Baixa o contentor.
4. Vira-se para a «esquerda» e desloca-se «em frente».

Além disso, cada fase dura exatamente um certo número de ciclos.

A atualização começa pelo tempo decorrido deste a atualização mais recente:

function update(ts) {
  const dt = 0.001 * (ts - this.last_ts);
  this.last_ts = ts;
  
  // Further instructions
}

Antes de se atualizar a contagem de ciclos (age) e outros atributos, é necessário tratar das pausas.

Pausas

Quando o modelo está em «pausa» os seus atributos não mudam.

Portanto, em modo «pausa», a atualização fica completa após ser processado this.last_ts:

function update(ts) {
  const dt = ts - this.last_ts;
  const last_ts = ts;

  if (this.paused) return;
  
  // Further instructions
}

A instrução

  if (this.paused) return;

impede que, quando this.paused é true, sejam atualizados os restantes atributos do modelo.

Caso contrário, se this.paused for false, o método update continua com a contagem de ciclos. Neste caso também importa contar os ciclos na fase atual:

function update(ts) {
  // Previous instructions
  
  this.age += 1;
  this.phase_age += 1;  
  
  // Further instructions
}

Fases

Em cada fase o modelo faz uma única animação.

Os atributos model.phase e model.phase_age controlam qual é a animação «ativa» e quantos ciclos decorreram nessa fase.

As fases controlam a animação «ativa» de acordo com a seguinte tabela:

Animação	Fase	Duração (ciclos)	Fase seguinte
camião para a direita	0	150	1
levantar contentor	1	50	2
baixar contentor	2	50	3
camião para a esquerda	3	150	0

function update(ts) {
  // Previous instructions
  
  if (this.phase === 0 && this.phase_age >= 150) {
    this.phase = 1;
    this.phase_age = 0;
  } else if (this.phase === 1 && this.phase_age >= 50) {
    this.phase = 2;
    this.phase_age = 0;
  } else if (this.phase === 2 && this.phase_age >= 50) {
    this.phase = 3;
    this.phase_age = 0;
    this.truck.tr.sx *= -1;
  } else if (this.phase === 3 && this.phase_age >= 150) {
    this.phase = 0;
    this.phase_age = 0;
    this.truck.tr.sx *= -1;
  }

  // Further instructions
}

Estas instruções verificam se a fase «ativa» expirou; nesse caso é «ativada» a fase seguinte.

Após a determinação da fase «ativa» são aplicadas as respetivas transformações

function update(ts) {
  // Previous instructions

  if (this.phase === 0) this.truck.tr.x += 0.01;
  if (this.phase === 1) this.bin.tr.alpha += 0.01 * Math.PI;
  if (this.phase === 2) this.bin.tr.alpha -= 0.01 * Math.PI;
  if (this.phase === 3) this.truck.tr.x -= 0.01;
}

e o modelo fica atualizado.

A Biblioteca do Modelo

A biblioteca do modelo junta as funções auxiliares, a inicialização e a atualização do modelo no ficheiro truck_model.js.

import { urect, ucirc, tid } from "minigrsys";
export { init_model };

function wheel(x, y) { ... }
function bin() { ... }
function truck() { ... }
function add_child(name, grobj) { ... }
function init_model() { ... }
function update(ts) { ... }

Esta biblioteca importa algumas funções do sistema gráfico, para facilitar a definição das formas e transformações dos objetos gráficos definidos aqui.

A única função exportada é init_model, que devolve um objeto que descreve o grafo de cena e com os atributos e métodos adequados à animação.

O HTML e o Ciclo de Animação

Esta animação existe num documento HTML com certos elementos presentes. O controlo da animação é definido numa função própria (main).

O mapa de importação define as referências para as bibliotecas:

<script type="importmap">
    {
        "imports": {
            "minigrsys": "./minigrsys.js",
            "model": "./truck_model.js",
            "main": "./refs_main.js"
        }
    }
</script>

A visualização decorre num elemento <canvas> e as mensagens de texto num <div>. Estes dois elementos são alinhados numa coluna:

<div style="
    display:grid;
    grid-template-columns:512px;
    margin:0 auto;
    width: fit-content">
    <div id="refs:terminal" style="
        font-family: monospace;
        padding:0.5em;
        background:black;
        color:seagreen">TERMINAL</div>
    <canvas id="refs:canvas"></canvas>
</div>

A animação inicia-se com a função main que tem como argumentos os id relevantes e o tamanho da visualização:

<script type="module">
    import { main } from "main";
    main("refs:canvas", "refs:terminal",
      512, 256);
</script>

O controlo da animação está definido na biblioteca refs_main.js, que importa (as bibliotecas para) o sistema gráfico e o modelo e exporta a função main, com:

• A inicialização do modelo e do contexto (sistema) gráfico.
• A definição do passo da animação (step).
• O início do ciclo de animação.

import { new_context } from "minigrsys";
import { init_model } from "model";

export { main };

function main(container_id, terminal_id, width, height) {
  
  const model = init_model();
  const context = new_context(container_id, terminal_id, width, height);
  
  function step(ts) {
    model.update(ts);
    context.render(model);
    context.print(
      `AGE: ${model.age} PHASE: ${model.phase} ${model.paused ? "PAUSED" : "RUNNING"}`,
    );
    requestAnimationFrame(step);
  }

  requestAnimationFrame(step);
}

Exercícios

1. As durações e sequências das fases da animação estão diretamente definidas na função update do modelo — isso é má prática. Melhore o modelo de forma a incluir as fases, as respetivas durações e a fase seguinte. Isto é:
   • Descreva cada fase com um objeto, por exemplo:

   {
     id: int,        // The Id of this phase
     duration: int,  // The target duration (in cycles)
     age: int,       // If active, the current duration
     next: int,      // The next phase
     action: (object) => { ... } // A function to execute
                     // at each update, when this phase is active
     start: (object) => { ... } // A function to execute
                     // when this phase becomes active
   }
   

   • Integre a gestão de uma lista de fases no método update do modelo.
   • Acrescente a definição das fases na inicialização do modelo.
2. Em vez das durações das animações serem controladas pelo número de ciclos, defina-as de forma a serem controladas, por exemplo, por uma posição «alvo» ou um ângulo «alvo».