Como se define a área de superfícies?

Na dimensão 0 a medida usual é a de contagem. Na dimensão 1 temos a noção de comprimento de uma curva no espaço como a do limite da soma do comprimento de linhas poligonais inscritas.

Mas como contamos a área de uma superfície, se nem sequer localmente a podemos planificar⁴? Que conceito afinal de volume é esse na dimensão 2 ou em dimensões superiores?

A resposta é hoje facilmente ultrapassada por meio da teoria da `métrica em variedades diferenciáveis' ou geometria riemanniana. Seja na geometria diferencial ou na física teórica, um tal instrumento não passa de uma idealização.

Abstraímos da realidade dos objectos físicos, com rigor matemático, um espaço vectorial tangente onde fazemos a geometria clássica e daí partimos para o estudo de fenómenos intrínsecos ou invariantes e, sob uma perspectiva nova, de propriedades globais⁵ dos espaços, seus subespaços e do movimento entre estes.

Suponhamos então que é dada uma porção de superfície ${\cal S}$ ou uma variedade de dimensão $n$ (conceito mais geral, mas a mesma ideia que em dim 2) como na figura 7.

Figura: Definimos espaço tangente $T_p{\cal S}$ no ponto $p$ sobre uma variedade ${\cal S}$ de dimensão $n$ independente da escolha das cartas. Por outro lado, escolher uma carta $\varphi$ significa escolher coordenadas. E adoptar o respectivo referencial tangente $\partial _i$ , $i=1,2,...$ .

Um espaço tangente em cada ponto $p\in{\cal S}$ está bem definido, em virtude de conhecermos as cartas do espaço dado. Ou seja, temos um atlas de ${\cal S}$ , que é um conjunto de cartas $\varphi:U\rightarrow {\mathbb{R}}^n$ com os $U$ subconjuntos abertos de ${\cal S}$ .

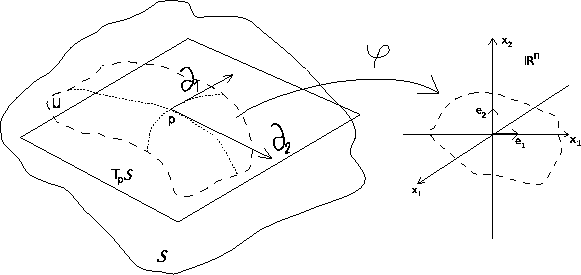Agora supomos que é dada a métrica, o instrumento matemático $\langle\,,\,\rangle$ que nos permite calcular ângulos,

$$\measuredangle(u,v)=\arccos\frac{\langle u,v\rangle}{\Vert u\Vert\Vert v\Vert},\ \quad\Vert u\Vert=\sqrt{\langle u,u\rangle},$$ (5)

$\forall u,v\in T_p{\cal S}$ . A métrica é dada por uma aplicação bilinear, simétrica e definida-positiva, isto é, um produto interno com valores em ${\mathbb{R}}$ . Se esta for razoável, então tem uma variação suave com $p$ , ou seja é de classe ${\mathrm{C}}^\infty_{}$ .

A métrica fica bem determinada numa carta local pelos valores $\langle\partial_i,\partial_j\rangle$ , $i,j=1,\ldots n$ . Recordemos que vectores $\partial _i$ , de classe ${\mathrm{C}}^\infty_{}$ por natureza, são induzidos em $T{\cal S}$ pela própria carta $\varphi$ . São campos vectoriais locais. Havendo necessidade, podê-mo-los denotar por $\partial_i^\varphi$ .

Seja $\varphi(p)=(x_1,\ldots,x_n),\ \forall p\in U$ , onde cada $x_i$ é função de $p$ . É fácil adivinhar que as cartas resultam em funções ${\mathrm{C}}^\infty_{}$ sobre as variedades, por construção, e que verificarão

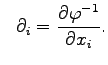$${\mathrm d}\varphi_p(\partial_i)=e_i, \ \ \partial_i=\frac{\partial{\varphi}^{-1}}{\partial x_i}.$$ (6)

Suponhamos agora que nos é dada outra carta qualquer $\psi$ com domínio (outro $U$ ) passando pelo domínio $U$ de $\varphi$ . Escrevamos $\psi(p)=(y_1,\ldots,y_n)$ . Então temos uma `lei de transformação natural' entre cartas na intersecção dos domínios

$$\partial_i^\varphi=\sum_{k=1}^n\frac{\partial y_k}{\partial x_i}\partial_k^\psi$$ (7)

e logo, por bilineariedade da métrica,

$$\langle\partial_i^\varphi,\partial_j^\varphi\rangle =\sum_{k,l=1}... ...\frac{\partial y_l}{\partial x_j}\langle\partial_k^\psi,\partial_l^\psi\rangle.$$ (8)

Note-se que esta equação nos dirá se temos uma métrica bem definida ou não: é importante que o tal aparelho para medir o espaço seja compatível com uma mudança de cartas, o que se verificará ou não pela equação (8).

Podemos escrever (8) em termos matriciais: se $G^\varphi$ é a matriz da métrica, ou seja, se $G^\varphi=[\langle\partial_i^\varphi,\partial_j^\varphi\rangle]_{i,j=1,\ldots,n}$ e $J$ é a matriz jacobiana $[\frac{\partial y_k}{\partial x_i}]$ , então aquela equação escreve-se

$$G^\varphi=J^tG^\psi J$$ (9)

com $J^t$ a matriz transposta de $J$ .

E temos finalmente em qualquer dimensão a definição

$${\mathrm{vol}}\,{\cal S}=\int_{\varphi(U)}\sqrt{\det G^\varphi}\,{\mathrm d}x_1\ldots{\mathrm d}x_n.$$ (10)

Nota importante: esta é a ideia essencial da definição de volume, pois surge um problema de domínio. Claro que aqui estamos apenas a integrar em $U$ esqueçendo o resto de ${\cal S}$ . Para chegar a todo o lado usaríamos partições da unidade, um dispositivo algo técnico que requer o seu tempo próprio.

Eis essencialmente como se chega hoje ao volume sabendo apenas o integral de Riemann, o qual é bem conhecido da Análise. (A história mostrará inclusive que este é que foi feito para aquele e não o contrário, como agora parece estarmos a pretender).

Teorema 4   ${\mathrm{vol}}\,{\cal S}$ não depende da escolha da carta.

Ressalvando a questão do domínio, este resultado vem de (9), de o determinante de um produto de matrizes ser o produto dos determinantes e de $\det J^t=\det J$ , donde

$$\begin{split}\int\sqrt{\det G^\varphi}\,{\mathrm d}x_1\ldots{... ...i}\,{\mathrm d}y_1\ldots{\mathrm d}y_n,\hspace{1cm} \end{split}$$ (11)

como queríamos. A última igualdade vem pela propriedade conhecida da mudança de variável no integral de Riemann (o fundamental que falta provar).

Note-se que a `forma diferencial' $\Omega_{\cal S}$ , de grau igual à dimensão de ${\cal S}$ ,

$$\Omega_{\cal S}(x)=\sqrt{\det G}\,{\mathrm d}x_1\wedge\ldots\wedge{\mathrm d}x_n,$$ (12)

$x\in{\cal S}$ , é já por si uma entidade bem definida pois é, de novo, independente da escolha das cartas. Utiliza-se aqui a álgebra exterior ou de Grassmann... $\Omega_{\cal S}$ é o elemento de área em dimensão 2 ou de volume em dim>2...