- ... estudado1
- Faça-se uma busca em http://arxiv.org/ com archimedes no título.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sempre2
- Sendo a sua efígie aquela que aparece nas célebres medalhas Fields.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Metodo,Enci,GraGui,Heath)3
- Outra importante referência no estudo de Arquimedes parece ser com certeza E. J. Dijkterhuis, cf. Archimedes, Munksgaard, Copenhaga, 1956, ou Princeton UP, 1987.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... planificar4
- Teríamos grande problema em provar que o limite da soma de áreas de faces poligonais inscritas numa qualquer superfície daria um invariante.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... globais5
- Este conceito não tem nada a ver com a famigerada `globalização' das relações humanas terrestres, apesar de muito falarmos da esfera.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... críticos6
- Aqueles
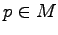 onde a característica de
onde a característica de
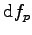 é menor que
é menor que 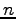 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... teorema7
- Se a função
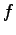 tiver como derivada
tiver como derivada
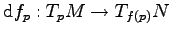 um isomorfismo em
um isomorfismo em 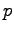 , então a função inversa
, então a função inversa 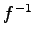 existe numa vizinhança de
existe numa vizinhança de 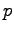 e é
e é
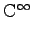 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.