Seguinte: Bibliografia Acima: Análise - Álgebra - Anterior: O grupo ortogonal
Agora voltemos à superfície esférica de raio 1 de dimensão ![]() , denotada por
, denotada por
![]() . Fixemos uma direcção
. Fixemos uma direcção ![]() qualquer perpendicular a um subespaço
qualquer perpendicular a um subespaço
![]() . O grupo ortogonal actua na esfera rodando-a sobre si mesma.
. O grupo ortogonal actua na esfera rodando-a sobre si mesma.
![]() actua como
actua como
![]() , uma função sobrejectiva,
, uma função sobrejectiva,
![]() e regular.
e regular.
Quais são os ![]() que fixam
que fixam ![]() ? São precisamente os que só rodam
? São precisamente os que só rodam
![]() , donde a escrita do `espaço simétrico'
, donde a escrita do `espaço simétrico'
Com algum cuidado pode-se provar que ![]() . Resulta então do teorema 6, chamemos-lhe de Fubini-Poincaré, lendo a fórmula (23), que
. Resulta então do teorema 6, chamemos-lhe de Fubini-Poincaré, lendo a fórmula (23), que
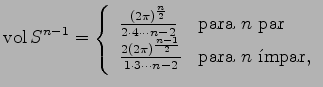 |
(27) |
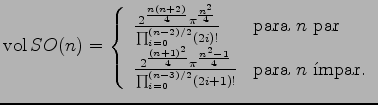 |
(28) |
rpa 2007-11-14