Sobre Autómatos e Linguagens de Programação
Em Autómatos e Linguagens de Programação faz-se uma introdução formal à teoria e às técnicas da análise e definição de linguagens de programação.
Os conceitos e as técnicas tratadas são ilustradas num capítulo final, onde é definida uma linguagem de programação simples e implementado um interpretador para essa linguagem.
Dado um programa python,
# file: guide.py
def resposta():
return 42
print(f"The answer is {resposta()}.\n")
Quando este programa corre, por exemplo
> python guide.py <enter>
> The answer is 42.
o que acontece entre o <enter> na linha python guide.py e aparecer o texto The answer is 42. na consola?
O interpretador do python, entre outras coisas:
- Lê o ficheiro
guide.pydo sistema de ficheiros. - Processa o conteúdo desse ficheiro de forma a determinar se corresponde a um programa válido (em
python, claro). - Executa as instruções desse programa, incluindo:
- A definição da função
resposta()e respetivas “sub-instruções”. - O cálculo do valor da expressão
"The answer is {resposta()}.\n". - Escrever na consola o valor dessa expressão.
- A definição da função
Outro exemplo: uma calculadora “básica”.
Para programar uma calculadora para a linha de comandos, o programa deve receber uma string com uma conta e escrever o respetivo resultado. Por exemplo > calc "2+3*4" deve escrever 14.
Quais são as dificuldades de fazer este programa? Há várias:
- Temos de saber verificar se o input está “bem formado”. Por exemplo
2+3*4está bem, mas+234**nem por isso… - Exatamente, o que “significa” cada “símbolo”?
2é 2? E se aparecer em20? - E como tratar “sequências” de símbolos?
2+3é sempre 2+3? Mas então2+3*4não devia ser14mas20…
Estas são exatamente as questões tratadas em ALP:
- Quais são os símbolos (ou letras) e as palavras válidas (isto é, as sequências de símbolos que sabemos tratar)?
- Como definir e representar todas as palavras válidas, isto é, a linguagem?
- Como distinguir as palavras válidas das inválidas?
- Como atribuir significado às palavras válidas? Isto é, como executar um programa?
Objetivos
Ao completar esta disciplina deve conseguir:
- Discutir máquinas de estados finitos.
- Construir expressões regulares, autómatos e gramáticas para aceitar/gerar linguagens especificadas; Converter entre representações equivalentes.
- Determinar o lugar de uma linguagem na Hierarquia de Chomsky e os principais problemas nas definições da sintaxe de linguagens de programação.
- Usar gramáticas formais para especificar a sintaxe de linguagens, ferramentas declarativas para gerar analisadores e scanners.
- Definir uma semântica formal e uma árvore de sintaxe abstrata para uma linguagem de programação simples.
- Explicar como os programas que processam outros programas tratam os outros programas e as vantagens de ter representações de programas.
- Escrever um programa para processar alguma representação de código.
Programa & Bibliografia
Programa
- Sobre ALP
- Objetivos
- Programa & Bibliografia
- Avaliação
- Palavras, Linguagens e Expressões Regulares
- Alfabetos, Palavras e Linguagens
- Expressões Regulares
- < Exercícios >
- Autómatos Finitos
- Autómatos Finitos Deterministas
- Computação Não-Determinista
- Minimização e Composição de AFD
- O Pumping Lemma
- < Exercícios >
- Gramáticas e Autómatos de Pilha
- Gramáticas Livres de Contexto
- Autómatos de Pilha
- < Exercícios >
- Análise Sintática
- Tipos de Análise Sintática
- Limpeza de uma Gramática
- < Exercícios >
- Gramáticas LL
- < Exercícios >
- Gramáticas LR
- < Exercícios >
- Representação & Execução de Programas
- Árvore de Sintaxe Abstrata
- Análise Semântica
- Suporte para um Interpretador
- < Exercícios >
Bibliografia
- Languages and Machines: An Introduction to the Theory of Computer Science, 2 ed. Thomas A. Sudkamp. Addison Wesley, 1997. (320 páginas)
- Compilers: Principles, Techniques and Tools, Alfred V. Aho, Ravi Sethi e Jeffrey D. Ullman. Addison Wesley, 1986. (1038 páginas)
Recursos
- Programação em
python:- Livro: How to Think Like a Computer Scientist: Learning with Python 3 Documentation.
- Tutorial: The Python Tutorial em
python.org. - Cheat Sheets: Várias.
- Simuladores AFD, AFnD, AP, GIC, ER, …
- OFLAT This tool is being developed at NOVA-LINCS (at the Computer Science Department of FCT-UNL) by the projects Factor and LEAFs and co-financed by Tezos Foundation and INRIA Foundation.
- Automata Learning Lab
- JFLAP is software for experimenting with formal languages topics including nondeterministic finite automata, nondeterministic pushdown automata, multi-tape Turing machines, several types of grammars, parsing, and L-systems.
ALisPé uma linguagem de programação usada para exemplificar a matéria de análise sintática.- Palavras Portuguesas (NAO) lista de 431114 palavras portuguesas, uma por linha.
Avaliação
- A avaliação de Autómatos e Linguagens de Programação consiste num exame, ou três frequências.
- As datas das provas são anunciadas no moodle.
- Se reprovar no exame normal pode fazer o exame de recurso.
- Todas as provas são opcionais e sem restrições (por exemplo, nota mínima).
Provas Orais — Em casos individuais que o docente ache necessário, pode ser realizada uma prova oral.
Aviso sobre Plágio ou Fraude
Fraude: Todo o comportamento do estudante em provas ou elementos de avaliação suscetível de desvirtuar o resultado da prova e adotado com a intenção de favorecer intencionalmente o próprio ou terceiros.
-
A fraude ou plágio cometidos em qualquer elemento de avaliação implica a anulação da prova e do seu resultado, sem prejuízo de eventual instauração de procedimento disciplinar.
-
São sanções aplicáveis às infrações disciplinares dos estudantes, de acordo com a sua gravidade:
- A advertência;
- A multa;
- A suspensão temporária das atividades escolares;
- A suspensão da avaliação escolar durante um ano;
- A interdição da frequência da instituição até cinco anos.
Referências
- Regulamento Académico da Universidade de Évora
- Regime jurídico das instituições de ensino superior
- Regulamento Disciplinar dos Estudantes da Universidade de Évora
Palavras, Linguagens e Expressões Regulares
 |
|---|
Neste capítulo são fixadas bases rigorosas para a definição de linguagens de programação e a análise dos respetivos programas.
É necessário começar por definir rigorosamente e sem ambiguidades, isto é, matematicamente, certos conceitos fundamentais como “símbolo” (ou “letra”), “palavra” e “linguagem”.
Também são definidas as “expressões regulares”, que permitem representar certas linguagens formais de forma compacta.
Com as “expressões regulares” tem-se uma forma rigorosa de definir certas linguagens formais. É o primeiro passo no processo para representar linguagens de programação.
Alfabetos, Palavras e Linguagens
Era uma vez, num reino muito muito distante, …
Símbolos e Alfabetos
Alfabeto, Símbolo. Um alfabeto é um conjunto finito de símbolos, também designados letras (em inglês: symbols, letters, tokens).
Os alfabetos são normalmente representados por maiúsculas gregas $\Sigma$ (sigma) e $\Gamma$ (gama) e os símbolos por minúsculas romanas $a, b, c, d$.
Por exemplo:
- O alfabeto do português tem os seguintes símbolos: $\tt a, b, c, \ldots, x, y, z$.
- Os símbolos $\tt 0$ e $\tt 1$ formam um alfabeto binário. Outro alfabeto binário muito usado em ALP é $\set{{\tt a}, {\tt b}}$.
- Os números naturais podem ser escritos em base 10 usando o alfabeto $ \set{\tt 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} $.
- Para as expressões algébricas usa-se o alfabeto $ \set{\tt 0, 1, \ldots, 8, 9} \cup \set{\tt +, -, \times, \div, (, )} $.
As linguagens de programação têm um conjunto de palavras reservadas, como
while,if, etc. que são atómicas, isto é, não podem ser divididas.O símbolo “
if” não é, em termos da linguagem de programação, um “i” seguido de um “f”, mas um símbolo que não pode ser decomposto.Já fragmentos de programas como
if (x == 42) { return "yes"; } else { return "no"; }são compostos. Nesta instrução condicional(x == 42)é o teste (ou guarda),{ return "yes"; }o bloco positivo e{ return "no"; }o bloco negativo. Neste caso a instrução resulta de uma regra do tipo
Condicional := if ( Condição ) { Instruções } else { Instruções }Por sua vez a guarda (
Condição) e os blocos deInstruçõespodem ser decompostos, até chegarmos a símbolos atómicos como(,==,return, etc.
Palavras
Palavra. Uma palavra sobre um alfabeto $\Sigma$ é uma sequência finita de símbolos desse alfabeto (em inglês: word).
Formalmente, uma palavra de comprimento $n$ é uma função $p: \set{1, 2 \ldots, n} \to \Sigma$ que a cada inteiro $i \in \set{1, 2, \ldots, n} \mapsto p(i) \in \Sigma$.
As palavras são normalmente representadas pelas minúsculas romanas $p, q, u, v, w, x, y, z$.
Palavra Vazia. A palavra vazia (em inglês: empty word, null, nil) é a única palavra de comprimento 0 e representa-se pela letra grega $\nil$ (lambda). Também é comum usar-se $\epsilon$ ou $\varepsilon$ (epsilon) para representar a palavra vazia.
Não confundir a palavra $\nil$ (que tem comprimento 0) com um símbolo. Estes, como palavras, têm comprimento um.
Propriedades do Comprimento das palavras
- O comprimento da palavra $p$ é normalmente representado por $|p|$.
- Para a palavra vazia, $|\nil| = 0$. Em geral, se $p = a_1 \cdots a_n$ então $|p| = n$. Isto é, $|a_1\cdots a_n| = n$.
Fecho de Kleene
Dado um alfabeto, interessa considerar todas as palavras que podem ser formadas com essas letras.
Por exemplo, para representar números em binário usam-se palavras sobre $\set{\tt 0, 1}$. Mas, depois de se definirem todas as palavras, há que determinar quais as que interessam. Por exemplo, embora $\tt 00$ e $\tt 0$ sejam palavras binárias (distintas), se interpretadas normalmente, ambas correspondem ao número $0$ e portanto há aqui uma ambiguidade. Será possível definir uma linguagem que continue a representar todos os números mas sem ambiguidades?
Para abordar estas questões tem de se começar por definir rigorosamente o conjunto de todas as palavras que se podem obter com um dado alfabeto.
Fecho de Kleene. O fecho do alfabeto $\Sigma$ é o conjunto de todas as palavras sobre $\Sigma$, representa-se por $\Sigma^\ast$ e fica definido pelas seguintes condições:
- base $\nil \in \Sigma^\ast$.
- passo Se $p \in \Sigma^\ast$ e $a \in \Sigma$ então $pa \in \Sigma^\ast$.
- fecho Qualquer palavra $p \in \Sigma^\ast$ só pode ser obtida por um número finito de aplicações do passo a começar na palavra vazia. E reciprocamente, qualquer palavra obtida a partir de $\nil$ por aplicações do passo em número finito está em $\Sigma^\ast$.
Esta definição exclui a possibilidade de palavras infinitas. Mas isto não significa que exista um limite ao comprimento das palavras em $\Sigma^\ast$. Pelo contrário, se $\Sigma \neq \emptyset$ então, para qualquer $n \in \mathbb{N}$ existe pelo menos uma palavra de comprimento $n$.
Exercício: Porquê? E porque é que acima é referida a condição “$\Sigma \neq \emptyset$”? O que é $\emptyset^\ast$?
No fecho de um alfabeto também ficam excluídas palavras formadas por símbolos de outros alfabetos. Por exemplo, a palavra $\tt abc$ não está em $\cl{\set{\tt a, b}}$.
Logo a primeira condição na definição de $\Sigma^\ast$ inclui a palavra vazia. Como muitas vezes é conveniente excluir $\nil$ define-se $$ \Sigma^+ = \cup_{n > 0} \Sigma^n = \Sigma \Sigma^\ast. $$
Exercício: Mostre que $\Sigma^+ = \Sigma^\ast \setminus \set{\nil}$.
Operações com Palavras
Comprimento
Ainda não foi apresentada uma definição rigorosa de comprimento de uma palavra. Usando um esquema recursivo:
Comprimento. A função comprimento é calculada pelas seguintes regras:
- base $|\nil| = 0$.
- passo $|pa| = |p| + 1$, com $p \in \Sigma^\ast, a \in \Sigma$.
Por exemplo, para calcular $\len{\tt abc}$:
- Como ${\tt abc}\ \neq\ \nil$, aplicar-se a regra do passo: fazendo $pa = {\tt abd}$ tem de ser $p = {\tt ab}$ e $a = {\tt c}$, e obtem-se $\len{\tt abc} = \len{\tt ab} + 1$.
- Ainda não está calculado o valor de $\len{\tt ab}$. Tornando a aplicar o passo: $\len{\tt ab} = \len{\tt a} + 1$.
- Uma nova aplicação do passo: $\len{\tt a} = \len{\nil} + 1$.
- Finalmente, pela base: $\len{\nil} = 0$, portanto $\len{\tt a} = 0 + 1 = 1$ e, sucessivamente, obtém-se $\len{\tt ab} = 2$ e $\len{\tt abc} = 3$.
Também é comum usar-se a notação $\len{p}_a$ para indicar o número de ocorrências do símbolo $a$ na palavra $p$.
Por exemplo: $\len{\tt aba}_{\tt a} = 2, \len{\tt aba}_{\tt b} = 1$.
Concatenação
O operação fundamental das palavras é a “concatenação”. A concatenação de hello com world é helloworld. Para definir rigorosamente esta operação:
Concatenação. A concatenação (ou produto) de duas palavras $u, v \in \Sigma^\ast$ representa-se por $u\cdot v$ ou apenas $uv$ e é uma operação binária definida por:
- base Se $v = \nil$ então $u\cdot v= u$.
- passo Se $|v| = n > 0$ então
- Existe uma palavra $w \in \Sigma^\ast$ e uma letra $a \in \Sigma$ tal que $v = wa$.
- $u\cdot v = (u\cdot w)a$.
Por exemplo, para calcular a concatenação de $\tt ab$ com $\tt cd$:
- O comprimento de $\tt cd$ é 2, portanto temos de aplicar o passo: ${\tt ab}\cdot{\tt cd} = ({\tt ab}\cdot {\tt c}){\tt d}$.
- Precisamos de calcular ${\tt ab}\cdot {\tt c}$. Pela regra do passo: ${\tt ab}\cdot {\tt c} = ({\tt ab}\cdot \nil) {\tt c}$.
- Finalmente, ${\tt ab}\cdot \nil$ é calculada pela regra base: ${\tt ab}\cdot \nil = {\tt ab}$.
- Andando para trás: ${\tt ab}\cdot {\tt c} = ({\tt ab}\cdot\nil){\tt c} = ({\tt ab}){\tt c} = {\tt abc}$ e, portanto, ${\tt ab}\cdot{\tt cd} = ({\tt ab}\cdot{\tt c}){\tt d} = {\tt abcd}$.
Potência
A repetição de concatenações define as potências, tal como a multiplicação dos números.
Potências. As potências da palavra $p \in \Sigma^\ast$ são (informalmente): $$ p^0 = \nil, p^1 = p, p^2 = pp, \ldots, p^n = p^{n-1}p. $$
Por exemplo, $({\tt 01})^2 = {\tt 0101}$ mas ${\tt 01}^2 = {\tt 011}$, seguindo as regras normais de precedência das operações.
Inversa
Finalmente, as palavras (enquanto sequências de símbolos) podem ser escritas “de trás para a frente”:
Inversa. A inversa de $p \in \Sigma^\ast$, representada por $p^R$ (ou $p^{-1}$) é calculada pelas seguintes regras:
- base Se $p = \nil$ então $p^R = p$.
- passo Se $|p| = n > 0$ então $p = qa, a \in \Sigma$ e $p^R = a q^R$.
Por exemplo, se $p = {\tt abcd}$ então $p^R = {\tt dcba}$.
Propriedades das Operações de Palavras
O que acontece à inversa de duas palavras concatenadas?
Para quaisquer palavras $u, v \in \cl{\Sigma}$, $$ (uv)^R = v^R u^R$$
Demonstração (informal): Se $u=\nil$ a conclusão é evidente. Caso contrário $u = u_1 u_2 \ldots u_n$ e $v = v_1 v_2 \ldots v_m$ com todos os $u_i, v_j \in \Sigma$. Então: $$ \begin{aligned} (uv)^R &= (u_1 u_2 \ldots u_n v_1 v_2 \ldots v_m)^R \cr &= v_m \ldots v_2 v_1 u_n \ldots u_2 u_1 \cr &= (v_m \ldots v_2 v_1)(u_n \ldots u_2 u_1) \cr &= v^R u^R\qquad\qquad\square \end{aligned} $$
O fecho também tem propriedades interessantes.
Se $\Sigma, \Gamma$ forem alfabetos,
- $\cl{\Sigma} = \cup_{n \geq 0} \Sigma^n$.
- $\Sigma \subseteq \cl{\Sigma}$.
- $\cl{\emptyset} = \set{\nil}$.
- Se $\Sigma \neq \emptyset$ então $\cl{\Sigma}$ é infinito.
- Se $\Sigma \subset \Gamma$ então $\cl{\Sigma} \subset \cl{\Gamma}$.
Por fim, a concatenação tem propriedades semelhantes às do produto (de números).
Sejam $u, v, w \in \cl{\Sigma}$.
- associativa $u(vw) = (uv)w$.
- elemento neutro $u\nil = \nil u = u$.
- não comutativa Em geral, $uv \neq vu$.
- aditiva $\len{uv} = \len{u} + \len{v}$.
- unicidade Cada palavra só pode ser escrita de uma única forma como concatenação de símbolos. Isto é, se $u = v$ e $u = u_1 \ldots u_n$ e $v = v_1 \ldots v_m$ então $n = m$ (mesmo comprimento) e $u_i = v_i$ para cada $i =1, \ldots, n$ (mesmos símbolos) .
Ordenações de Palavras
Uma palavra pode “conter” outra. Por exemplo, palavra contém pala no início, ala no “meio” e lavra no fim. Estes três casos ilustram as definições que se seguem:
Subpalavra, prefixo, sufixo. Sejam $p, q, u, v \in \cl{\Sigma}$.
- subpalavra $p \leq q$ se $q = upv$.
- prefixo $p \leq_P q$ se $q = pv$.
- sufixo $p \leq_S q$ se $q = up$.
Fica claro que os prefixos são casos particulares das subpalavras (quando $u = \nil$) e que cada palavra é subpalavra de si própria (quando $u = \nil = v$).
Outro caso importante é a ordem lexicográfica (dos dicionários), onde se usa a ordem das letras para ordenar as palavras.
Ordem Lexicográfica. Supondo que o alfabeto está ordenado, $\Sigma = \set{a_1 < a_2 < \cdots < a_n}$. Então $p \leq_L q$ se:
- $p \leq_P q$.
- Caso contrário, $p = us_iv$ e $q = us_jw$ com $s_i < s_j$.
Esta definição abrange dois casos:
por < porqueporqueporé um prefixo deporque.porque < portugalporque, comoporque = por_q_ueeportugal = por_t_ugalentãoportugaleporquetêm um prefixo comum,por, e “divergem primeiro” nas letrasqet. Comoq < tentãoporque < portugal.
A ordem lexicográfica tem um problema interessante: Quantas palavras existem entre $\tt 0$ e $\tt 1$, num alfabeto binário?
Por exemplo ${\tt 00} <_L {\tt 1}$ [Exercício: porquê?]. Mas também ${\tt 000} < {\tt 1}$. De facto, ${\tt 0}^n < {\tt 1}$ para qualquer $n > 0$. Portanto, seguindo a ordem lexicográfica, há infinitas palavras entre $\tt 0$ e $\tt 1$.
Esta conclusão, embora dramática, mostra que a ordem lexicográfica é inútil na importante tarefa de enumerar (isto é, listar) todas as palavras por ordem. Para resolver este problema é necessária mais uma ordem entre palavras:
Ordem Mista. Dadas duas palavras $p, q \in \cl{\Sigma}$, $p \leq_M q$ se $\len{p} < \len{q}$ ou ($\len{p} = \len{q}$ e $p \leq_L q$).
Dito de outra forma, a ordem mista define o seguinte processo:
- Primeiro, as palavras são agrupadas por comprimentos iguais: todas as palavras de comprimento 0 antes das de comprimento 1, todas as de comprimento 1 antes das de 2, etc.
- Depois, em cada grupo, as palavras (todas com o mesmo comprimento) são ordenadas lexicograficamente.
Revisitando o exemplo anterior:
- $\tt 0$ e $\tt 1$ têm o mesmo comprimento. Portanto, são comparadas lexicograficamente: ${\tt 0} <_M {\tt 1}$ porque ${\tt 0} <_L {\tt 1}$ .
- O comprimento de $\tt 00$ é maior que o de $\tt 1$. Portanto, ${\tt 1} <_M {\tt 00}$.
- $\tt 01$ e $\tt 10$ têm o mesmo comprimento. Lexicograficamente, ${\tt 01} <_L {\tt 10}$ portanto ${\tt 01} <_M {\tt 10}$.
De facto a ordem mista é uma ferramenta essencial porque permite “avançar passo-a-passo” no conjunto de todas as palavras, sem deixar nenhuma de fora. Mais concretamente:
A ordem mista define uma sequência de todas as palavras. No caso do alfabeto binário, com $\tt 0 < 1$:
$$ \nil <_M {\tt 0} <_M {\tt 1} <_M {\tt 00} <_M {\tt 01} <_M {\tt 10} <_M {\tt 11} <_M {\tt 000} <_M \cdots $$
Sucessor
A ordem mista permite começar na primeira palavra, avançar para a seguinte, depois para a seguinte, etc. da mesma forma são contados os números: 0, 1, 2, etc.
A passagem de um número para o seguinte (x++) tem nome, sucessor, que também se aplica às palavras:
Sucessor. Seja $\Sigma = \set{a_1 < a_2 < \cdots < a_n}$ um alfabeto ordenado. A função sucessor tem assinatura $\sigma: \cl{\Sigma} \to \cl{\Sigma}$ e calcula-se pelas seguintes regras:
- base $\sigma(\nil) = a_1$.
- passo Se $i < n$ então $\sigma(pa_i) = pa_{i + 1}$. Caso contrário, $\sigma(pa_n) = \sigma(p)a_1$.
Voltando ao exemplo anterior: $$ \sigma(\nil) = {\tt 0}, \sigma({\tt 0}) = {\tt 1}, \sigma({\tt 1}) = \sigma(\nil){\tt 0} = {\tt 00}, \ldots $$
Visto de outra forma, usando o sucessor obtém-se uma sequência que começa na palavra vazia e percorre todas as palavras:
$$ \nil \stackrel{\sigma}{\rightarrow} {\tt 0} \stackrel{\sigma}{\rightarrow} {\tt 1} \stackrel{\sigma}{\rightarrow} {\tt 00} \stackrel{\sigma}{\rightarrow} \cdots $$
Há uma clara relação entre a ordem mista e a função sucessor.
Seja $p_0 <_M p_1 <_M p_2 <_M \ldots$ a sequência de todas as palavras de $\cl{\Sigma}$ que se obtém com a ordem mista e $p \in \cl{\Sigma}$ uma palavra qualquer.
- $p <_M \sigma(p)$.
- Se $p \neq \nil$ então existe uma palavra $q\in\cl{\Sigma}$ tal que $p = \sigma(q)$.
- $p_{i+1} = \sigma(p_i)$.
O que este teorema afirma, especialmente na igualdade $p_{i+1} = \sigma(p_i)$, é que a ordem mista e a função sucessor são aspetos diferentes da mesma enumeração das palavras.
Linguagens
Numa linguagem de programação nem todas as palavras possíveis correspondem a programas válidos. Por exemplo:
2 return) *
: dobro def (x
é uma palavra que pode ser formada com o alfabeto do python, mas não é um programa.
É necessário, de alguma forma, distinguir as palavras que são “válidas” das outras que não o são. De novo, encontramos na matemática exatamente as ferramentas necessárias.
Linguagem. Uma linguagem é um conjunto de palavras sobre um certo alfabeto. Isto é, $A$ é uma linguagem sobre $\Sigma$ se $A \subseteq \cl{\Sigma}$.
Esta definição de linguagem parece dizer pouco, mas por enquanto serve exatamente para o que se pretende.
Por exemplo, se $\Pi$ for a linguagem dos programas python então ${\tt print(2 + 40)} \in \Pi$ mas ${\tt +)\ 40 print\ 2\ (} \not \in \Pi$.
Mais tarde será enunciado e tratado o Problema Principal de ALP:
Problema Principal de ALP (versão 0). Dada uma linguagem $A$ e uma palavra $p$ no mesmo alfabeto, determinar se $p \in A$.
Entretanto, como uma linguagem é (apenas) um conjunto de palavras, tem um certo número de elementos, que pode ser infinito (quantos programas python existem?): Se $A$ for uma linguagem, $\len{A}$ representa o número de elementos de $A$.
Outros exemplos de linguagens são:
- binárias $\set{\tt 0, 1}$, $\set{\tt \nil, 0, 00, 000, \ldots}$, etc.
- As palavras do português, sobre o alfabeto romano. Por exemplo,
a,aba,abade, etc. mas nãoaa,prof,tásse,xkcd, etc. - Os programas de uma linguagem de programação.
- As frases do português, sobre o alfabeto formado pelas palavras do português. Por exemplo
bom dia,a aula é longa, etc. mas nãodia dia dia,aula a é longa, etc.
Muitas vezes é útil visualizar-se uma linguagem de forma a explorar a estrutura das suas palavras. Isso pode ser feito através de árvores:
Árvore de uma Linguagem. Seja $A \subseteq \cl{\Sigma}$ uma linguagem sobre $\Sigma$.
Os vértices (ou nós) da árvore de $A$ (ou diagrama de $A$) são palavras de $\cl{\Sigma}$ e cada aresta (ou arco) tem um símbolo de $\Sigma$. Além disso, todas as arestas são da seguinte forma: se $p\in\cl{\Sigma}$ e $a \in \Sigma$ então $p \stackrel{a}{\rightarrow} pa$ é uma aresta. A raíz da árvore é a palavra vazia.
Cada vértice é representado por um círculo com a respetiva palavra lá dentro. Uma palavra da linguagem $A$ é representada por um círculo duplo.
Por exemplo, $A = \set{\tt 01, 011, 11, 101} \subseteq \cl{\set{\tt 0, 1}}$ tem a seguinte árvore (onde os vértices irrelevantes foram omitidos):
| Árvore (parcial) de $A = \set{\tt 01, 011, 11, 101}$ |
|---|
 |
| As palavras de $A$ estão em círculos duplos. |
Operações com Linguagens
Como conjuntos, as linguagens podem ser combinadas pelas operações comuns: união, intersecção, etc. Além disso, como os seus elementos são palavras, podem ser definidas operações adicionais, específicas das linguagens (concatenação, fecho, etc).
Operações com Linguagens. Sejam $A, B$ linguagens sobre $\Sigma$. Estão definidas as seguintes operações de conjuntos:
- união $A \cup B = \set{p: p \in A \lor p \in B}$.
- intersecção $A \cap B = \set{p: p \in A \land p \in B}$.
- subtração $A \setminus B = \set{p: p \in A \land p \not\in B}$.
- complemento $\overline{A} = \cl{\Sigma} \setminus A$.
Adicionalmente, usando as operações de palavras:
- concatenação $A B = \set{pq: p \in A \land q \in B}$.
- potências $A^0 = \set{\nil},\ A^1 = A,\ A^2 = AA,\ \ldots,\ A^{n+1} = A A^n$.
- fechos $\cl{A} = A^0 \cup A^1 \cup A^2 \cup \cdots,\ A^+ = A\cl{A}$.
- inversão $A^R = \set{p^R: p \in A}$.
Alguns exemplos das operações específicas das linguagens: Sejam $A = \set{\tt a, b, ac}, B= \set{\tt \nil, a, c}$. Então:
- $AB = \set{\tt a, b, ac}\set{\tt \nil, a, c} = \set{\tt a\nil, aa, ac, b\nil, ba, bc, ac\nil, aca, acc} = \set{\tt a, aa, ac, b, ba, bc, aca, acc}$.
- As palavras de $AB$ foram formadas escolhendo primeiro uma palavra de $A$ e depois uma palavra de $B$.
- A palavra $\tt ac$ pode ser obtida de suas formas: $\tt a \cdot c$ e $\tt \nil \cdot ac$.
- $B^2 = BB = \set{\tt \nil, a, c}\set{\tt \nil, a, c} = \set{\tt \nil, a, c, aa, ac, ca, cc}$.
- $A^0 = \set{\nil}; A^2 = \set{\tt aa, ab, aac, ba, bb, bac, aca, acb, acac}, \ldots$.
- $A^R = \set{\tt a, b, ca},\ B^R=\set{\tt \nil, a, c} = B$.
Confusões com a palavra vazia, o conjunto vazio, etc.
- A palavra vazia, $\nil$, não é um símbolo. Qualquer símbolo, como palavra, tem comprimento 1. A palavra vazia tem comprimento 0.
- O conjunto vazio, $\emptyset$, tem 0 elementos. Para tornar este facto mais explícito também se escreve $\emptyset = \set{}$.
- O conjunto $\set{\nil}$ tem um elemento, $\nil$. Portanto, não é o conjunto vazio.
Exemplo. Aqui (e só no âmbito deste exemplo) estamos a distinguir explicitamente os símbolos usando plicas, como em 'a', e as palavras usando aspas, como em "ab".
- O alfabeto
{a, b}tem dois símbolos:'a'e'b'. - Uma palavra é uma (qualquer) sequência finita de símbolos.
- Por exemplo
"abba","baba","aa", etc.
- Por exemplo
- Todas as palavras de comprimento 2 são
"aa","ab","ba","bb". - Também poderíamos listar todas as palavras de comprimento 3 (num total de oito palavras), etc.
- Todas as palavras de comprimento 1 são
"a"e"b".- Se quiséssemos ser terrivelmente rigorosos, teríamos de dizer que
'a'e"a"são diferentes porque'a'é um símbolo e"a"é uma sequência de símbolos, tal como, por exemplo, o inteiro1é completamente diferente de[1], que é uma lista de inteiros. - Raramente é necessário distinguir explicitamente os símbolos das palavras de comprimento um.
- Se quiséssemos ser terrivelmente rigorosos, teríamos de dizer que
- Só há uma palavra com comprimento zero. Como sequência,
""é a (única) com zero símbolos. Em vez de""escreve-seλ(ouεouϵ).λnão é um símbolo mas uma palavra. Escrita por extenso é"".
- Usando a concatenação de palavras podemos escrever, por exemplo:
"abba" = "ab" · "ba".- Outras formas de obter
"abba"são"abba" = "a" · "bba","abba" = "abb" · "a", etc. - Em particular também
"abba" = "abba" · λou"abba" = λ · "abba"ou mesmo"abba" = λ · "a" · λ · "bba". - Nestes exemplos o
λnunca aparece entre"..."pois isso é o equivalente a um erro sintático. Também não escrevemos2 */ 3quando fazemos contas…
- Outras formas de obter
- Em geral não se escrevem os símbolos como
'a', as palavras como"abab"nem as concatenações como"aa" · "ba".- Portanto, em vez de
"abba" = λ · "a" · λ · "bba"o que escrevemos é simplesmenteabba = λaλbba. - Este abuso de notação pode facilitar a leitura errada de
λcomo um símbolo, à semelhança deaeb.
- Portanto, em vez de
Linguagens e Expressões Regulares
Uma forma de especificar linguagens formalmente.
Na secção anterior observou-se que para definir uma linguagem de programação o fecho, $\cl{\Sigma}$, não é adequado porque tem “demasiadas” palavras.
Mais precisamente, a situação é a seguinte:
Para definir uma linguagem de programação começa-se for escolher um certo alfabeto e, sobre esse alfabeto, define-se uma linguagem cujas palavras são exatamente os programas válidos da linguagem de programação.
O Problema Principal de ALP (versão 0) – Dada uma linguagem $A$ e uma palavra $p$ no mesmo alfabeto, determinar se $p \in A$ – não desenvolve condições para determinar $p \in A$. É necessário um “sistema” que permita definir linguagens formais e que seja:
- Computável: Existe um algoritmo que recebe como entrada uma palavra $p$ e ao fim de um número finito de passos produz uma resposta
simounãoconforme $p \in A$ ou não. - Eficiente: O número de passos referido no passo anterior não deve ser “muito maior” que o comprimento da palavra.
- Adequado: Deve ser possível definir (os programas de) qualquer linguagem de programação.
Portanto:
Problema Principal de ALP (versão 1): Determinar um sistema computável e eficiente para determinar se $p \in A$ e que seja adequado (i.e., $A$ é uma linguagem de programação).
Linguagens Regulares
As operações entre linguagens (principalmente, a união, a concatenação e o fecho) permitem começar por linguagens muito simples e definir formalmente, rigorosamente, sem ambiguidades, linguagens mais complexas. Por exemplo, a partir do alfabeto binário $\set{\tt 0, 1}$, a linguagem das palavras com um número par de $\tt 1$ é $\cl{\set{\tt 0, 11}}$.
O ênfase em “formal, rigoroso, não ambíguo” é necessário para resolver algoritmicamente o Problema Principal de ALP. Mais especificamente, pretende-se obter um programa que tem como entrada uma especificação formal de uma linguagem e que produz um segundo programa que tem como entrada uma palavra e que determina se essa palavra pertence, ou não, à linguagem dada ao primeiro programa. Isto é, pretende-se definir um programa Super tal que
- Se
efor uma especificação formal de uma linguagem de programaçãoL:PL = Super(e). - Seja
puma palavra.PL(p)éverdadeoufalsoconformep in Lou não. - Tanto
SuperquantoPLdevem ser eficientes.
O Problema Principal de ALP, nas suas várias versões, trata de encontrar uma “especificação formal” adequada e obter os programas Super e PL. De facto, a resolução seguida em ALP até vai mais longe: A resposta a $p \in A$ é calculada de forma que quando $p$ for um programa válido (isto é, “$p \in A$” é verdade) também se obtém uma “representação intermédia” de $p$, apta a ser executada.
Por enquanto define-se a classe das linguagens regulares:
Linguagem Regular (LR). Seja $\Sigma$ um alfabeto. Uma linguagem regular sobre $\Sigma$ define-se recursivamente pelas seguintes regras:
- base Os conjuntos $\empty, \set{\nil}$ e, para cada $a \in \Sigma,\ \set{a}$ são linguagens regulares.
- passo Se $A$ e $B$ forem linguagens regulares então $A\cup B, AB, \cl{A}$ também são linguagens regulares.
- fecho Um conjunto de palavras é uma linguagem regular se, e só se, pode ser definido através de um número finito de aplicações do passo a partir dos conjuntos da base.
Alguns exemplos de linguagens regulares:
- $\set{\tt 001, 110} = \set{\tt 0}\set{\tt 0}\set{\tt 1} \cup \set{\tt 1}\set{\tt 1}\set{\tt 0}$.
- Qualquer linguagem finita.
- O conjunto das palavras que começam em $\tt 0$ é infinito mas regular: $\set{\tt 0}\cl{\set{\tt 0, 1}}$.
Expressões Regulares
A notação usual dos conjuntos, com $\set{}, \del{}$, etc. torna difícil escrever e ler linguagens regulares. Para aliviar esse problema usa-se uma notação específica.
Expressão Regular (ER). Seja $\Sigma$ um alfabeto. Uma expressão regular sobre $\Sigma$ define-se recursivamente pelas seguintes regras:
- base As expressões vazio $\empty$, palavra vazia $\nil$ e, para cada $a \in \Sigma,\ a$ são expressões regulares.
- passo Se $a$ e $b$ forem expressões regulares então a união $a \cup b$, a concatenação (ou produto) $a\cdot b$ e a iteração $\cl{a}$ também são expressões regulares.
- fecho Uma expressão é uma expressão regular se, e só se, pode ser definida através de um número finito de aplicações do passo a partir das expressões da base.
Alguns exemplos de expressões regulares:
- $001\cup 110 \simeq (0 \cdot (0 \cdot 1)) \cup ((1\cdot 1) \cdot 0)$.
- Qualquer palavra de $\cl{\Sigma}$.
- $0 \cdot \cl{(0 \cup1)}$.
Antes de avançar no estudo das ER e LR é importante esclarecer o seguinte ponto importante sobre a notação das expressões regulares:
Regras de Simplificação das Expressões Regulares. A escrita completa de uma expressão regular pode (ainda) ser confusa, por causa dos parêntesis:
$$ (\cl{0} \cup (1 \cdot 0 \cdot (\cl{0}))) \cdot 1 \cdot (\cl{0}) \cdot (((0 \cdot (\cl{1}) \cup (\cl{1})))) $$
Para simplificar esta escrita usam-se as seguintes regras de simplificação:
- Sempre que possível não se usa o símbolo da concatenação. Isto é, em vez de $x \cdot y$ escreve-se $xy$.
- A iteração $\cl{}$ tem precedência sobre $\cdot$ e sobre $\cup$. Isto é, $0\cdot \cl{1}$ é $0\cdot (\cl{1})$, não $\cl{(0\cdot 1)}$. Igualmente,$0\cup \cl{1}$ é $0\cup (\cl{1})$, não $\cl{(0\cup 1)}$.
- A concatenação $\cdot$ tem precedência sobre a união $\cup$. Isto é, $a\cup b\cdot c$ é $a \cup (b \cdot c)$, não $(a \cup b) \cdot c$.
Com estas regras a ER acima fica com o seguinte aspeto: $$ (\cl{0}\cup 10\cl{0})1\cl{0}(0\cl{1}\cup\cl{1}) $$
Diagramas das Expressões Regulares
As expressões regulares podem ser representadas por um diagrama gráfico cuja visualização pode ajudar a entender a sua estrutura.
Diagrama de uma Expressão Regular (Diagrama de Wirth). O diagrama de uma expressão regular é um grafo orientado definido para as operações base e passo da seguinte forma:
Forma da Expressão Regular Tipo Sub-Grafo $a$ símbolo ou $\lambda$ $xy$ concatenação $x\cup y$ união $\cl{x}$ iteração
Por exemplo, o diagrama da expressão regular $\cl{(11 \cup 0)}\cl{(00 \cup 1)}$ pode ser obtido da seguinte forma:
| Operação | Diagrama |
|---|---|
| Início |  |
| Concatenação |  |
| Iterações |  |
| Uniões |  |
No diagrama final há várias arestas que podem ser eliminadas e ainda continuar a representar a expressão regular inicial. Por exemplo, uma das duas arestas $\nil$ consecutivas, no cento do diagrama, pode ser eliminada.
| Operação | Diagrama |
|---|---|
| Simplificação |  |
Neste caso foi simples detetar uma aresta que podia ser eliminada. Em geral, quais são as arestas que podem ser eliminadas?
Teorema da Eliminação de Arestas Vazias. A aresta
pode ser eliminada se:
- O vértice $\alpha$ não é final e não saem mais arestas de $\alpha$ ou
- O vértice $\beta$ não é inicial e não entram mais arestas em $\beta$.
Alternativamente, a aresta não pode ser eliminada se:
- O vértice $\alpha$ é final ou saem mais arestas de $\alpha$ e
- O vértice $\beta$ é inicial ou entram mais arestas em $\beta$.
Usando o teorema da eliminação de arestas vazias:
| Operação | Diagrama |
|---|---|
| Simplificação (II) |  |
Semântica das Expressões Regulares
O número quatro pode ser referido de várias formas: IV, 100, 4, quatro, 2+2, etc. Todas essas formas são expressões – texto, sintaxe – cuja interpretação – significado, semântica – é um certo objeto abstrato.
Esta é também a relação entre as linguagens regulares e as expressões regulares: As linguagens são conjuntos (objetos matemáticos, abstratos) que podem ser representados por certas expressões. Isto é, a semântica das ER são as LR. Reciprocamente, as ER são uma sintaxe para as LR. Mais precisamente:
Linguagem Representada por uma Expressão Regular. Qualquer expressão regular sobre $\Sigma$ representa uma certa linguagem, definida pelas seguintes regras:
- $L(\empty) = \empty$.
- $L(\nil) = \set{\nil}$.
- Para cada $a \in \Sigma, L(a) = \set{a}$.
- Se $x$ for uma expressão regular então $L(\cl{x}) = \cl{L(x)}$.
- Se $x, y$ forem expressões regulares então $L(x \cup y) = L(x) \cup L(y)$.
- Se $x, y$ forem expressões regulares então $L(xy) = L(x) L(y)$.
Até aqui, e neste enunciado em particular, estão a ser usados os mesmos símbolos (sintaxe), por exemplo $\empty, \cup, \cl{}$ com significados (semântica) muito diferentes. Por exemplo, “$\cup$” numa ER é apenas um símbolo que liga outras ERs — da mesma forma que + liga \quaddois números\quad duas expressões numéricas. Mas “$\cup$” numa LR é uma operação entre conjuntos, que tem um valor bem definido — tal como 2 + 2 tem um valor bem definido (sob as convenções comuns).
Além disso, foi apenas definida uma função entre ERs e certos conjuntos de palavras – nada afirma, até aqui, que $L(x)$ é regular. Isto é, se $x$ for uma expressão regular então $L(x)$ é uma linguagem. A relação com as linguagens regulares fica esclarecida a seguir:
Equivalência de Expressões e Linguagens Regulares.
- Cada expressão regular representa uma linguagem regular. Mais especificamente: Se $x$ for uma expressão regular sobre $\Sigma$ então $L(x)$ é uma linguagem regular sobre $\Sigma$.
- Cada linguagem regular pode ser representada por uma expressão regular. Mais especificamente: Se $A$ for uma linguagem regular sobre $\Sigma$ então existe uma expressão regular sobre $\Sigma$, $x$, tal que $A = L(x)$.
Isto é, as expressões regulares denotam exatamente as linguagens regulares e a relação entre umas e outras é a função $L$. Dito de outra forma, as LR são a semântica associada às ER e, reciprocamente, as ER proporcionam uma sintaxe para as LR.
Por exemplo, a linguagem dos inteiros sem sinal e sem $0$ à esquerda (isto é, a representação binária dos números inteiros positivos):
$$ \begin{aligned} \set{0, 1, 10, 11, 100, 101, \ldots} &= \set{0} \cup \set{1}\set{\nil, 0, 1, 00, 01, \ldots} \cr &= \set{0} \cup \set{1}\cl{\set{0, 1}}\cr &= L(0 \cup 1\cl{(0 \cup 1)}) \end{aligned} $$
Há ainda outro tipo importante de equivalência: Depois de fixado o conjunto de símbolos e de operações, duas expressões (sintaxes) muito diferentes podem ter o mesmo valor (semântica).
Por exemplo o número quatro (o objeto matemático abstrato) pode ser representado pelas expressões $4$, $2+2$, $2^2$, etc. Nestes casos escreve-se $2+2 = 4$, $2^2 = 4$ etc. Mas em ALP é preciso cuidado com o sinal “$=$”. As expressões “$4$” e “$2+2$” são sintaticamente diferentes (por exemplo, porque “$4$” tem apenas um símbolo e “$2+2$” tem três) mas equivalentes (a mesma semântica).
Nas linguagens regulares “$A = B$” representa a igualdade entre conjuntos, uma relação matemática. No caso das expressões regulares é necessário esclarecer se se trata de igualdade sintática ou de uma equivalência (isto é, uma igualdade semântica). Por exemplo, $0 \cup 1$ e $1 \cup 0$ são diferentes ao nível sintático: diferem logo no primeiro símbolo. Mas ambas representam a mesma linguagem regular, o conjunto $\set{0, 1}$. Isto é, $L(0 \cup 1) = L(1 \cup 0)$.
Equivalência de Expressões Regulares. Duas expressões regulares, $x, y$, sobre $\Sigma$ são equivalentes, $x \equiv y$, se $L(x) = L(y)$.
No uso comum de expressões regulares pretende-se usar a equivalência, não a igualdade sintática, pelo que “$x = y$” normalmente representa a equivalência, apesar de esta escrita ser um abuso da notação. Isto é, escreve-se $0 \cup 1 = 1 \cup 0$ em vez de $0 \cup 1 \equiv 1 \cup 0$, porque é mais conveniente. Os casos em que se trata a igualdade sintática devem ser explicitamente assinalados como tais.
Propriedades das Expressões Regulares
Sejam $x, y, z$ expressões regulares sobre o alfabeto $\Sigma$. Considerando as operações de união e concatenação:
$$ \begin{aligned} x \cup (y \cup z) &= (x \cup y) \cup z & x(yz) &= (xy)z \cr x \cup \empty &= \empty \cup x = x & x\nil &= \nil x = x \cr && x\empty &= \empty x = \empty \cr x \cup y &= y \cup x \cr x \cup x &= x \cr x(y \cup x) &= xy \cup xz & (x \cup y)z &= xz \cup yz \end{aligned} $$
Para o fecho:
$$ \begin{aligned} \cl{\empty} &= \nil & \cl{\nil} &= \nil \cr \cl{\del{\cl{x}}} &= \cl{x} & \cl{x} &= \nil \cup x\cl{x} \cr x\cl{\del{yx}} &= \cl{\del{xy}} x \cr \cl{\del{x \cup y}} &= \cl{\del{\cl{x} \cup y}} \cr &= \cl{x}\cl{\del{x \cup y}} \cr &= \cl{\del{x \cup y\cl{x}}} \cr &= \cl{(\cl{x}\cl{y})} \cr &= \cl{(\cl{x}y)}\cl{x} \cr &= \cl{x}\cl{(y\cl{x})} \end{aligned} $$
Com estas equivalências uma ER inicialmente complicada (isto é, comprida e/ou profunda) pode ser simplificada. Um exemplo imediato é $\cl{(\cl{(\cl{a})})} = \cl{a}$. Outro exemplo:
$$ a\AST (b \cup (a\AST b\AST)\AST) \alert{a} a\AST (ba\AST)\AST \alert{b} \stackrel{?}{=} (a \cup b)\AST \alert{a}(a \cup b)\AST \alert{b} $$
Aplicando as regras de equivalência $$ \begin{aligned} &a\AST (b \cup \alert{(a\AST b\AST)\AST}) a a\AST (ba\AST)\AST b = & (x\AST y\AST)\AST = (x \cup y)\AST \cr &= a\AST \alert{(b \cup(a \cup b)\AST)} a a\AST (ba\AST)\AST b & y \cup (x \cup y)\AST = (x \cup y)\AST \text{(porquê?)} \cr &= \alert{a\AST (a \cup b)\AST} a a\AST (ba\AST)\AST b & x\AST (x \cup y)\AST = (x \cup y)\AST \cr &= (a \cup b)\AST a \alert{a\AST (ba\AST)\AST} b & x\AST (y x\AST)\AST = (x \cup y)\AST \cr &= (a \cup b)\AST a (a \cup b)\AST b & \text{aceitável… continuando:}\cr &\stackrel{?}{=} \alert{b\AST a} (b\cup a)\AST b \end{aligned} $$
$$ \begin{aligned} &= \alert{(a \cup b)\AST} a (a \cup b)\AST b & x \cup y = y \cup x \cr &= \alert{(b \cup a)\AST} a (a \cup b)\AST b & (x \cup y)\AST = x\AST (y x\AST)\AST \cr &= b\AST\alert{(ab\AST)\AST a} (a \cup b)\AST b & (xy)\AST x= x(yx)\AST \cr &= b\AST a(b\AST a)\AST \alert{(a \cup b)\AST} b & x \cup y = y \cup x \cr &= b\AST a(b\AST a)\AST \alert{(b \cup a)\AST} b & (x \cup y)\AST = (x\AST y)\AST x\AST \cr &= b\AST a\alert{(b\AST a)\AST (b \AST a)\AST} b\AST b & x\AST x\AST = x\AST \text{(porquê?)} \cr &= b\AST a\alert{(b\AST a)\AST b\AST} b & (x\AST y)\AST x\AST = (x \cup y)\AST \cr &= b\AST a (b\cup a)\AST b \end{aligned} $$
As linguagens e expressões regulares são o passo atual para resolver o Problema Principal de ALP (versão 1) – Determinar um sistema computável, eficiente e adequado para definir linguagens de programação.
Nesse sentido importa responder às seguintes questões:
- Dada uma linguagem regular $A$, como obter um sistema computável e eficiente para determinar se $p \in A$?
- As linguagens regulares são adequadas para definir todas as linguagens de programação? Por exemplo, será possível definir a sintaxe dos programas
PythonouJavausando apenas expressões regulares?
Estas questões são resolvidas no próximo capítulo, Autómatos Finitos, onde é definido e estudado um modelo abstrato de computador simples e como este se relaciona com as ER e LR.
Palavras, Linguagens e Expressões Regulares — Exercícios
| Otimização Prematura |
|---|
 |
| O xkcd obrigatório. |
Indicações gerais para os exercícios de implementação
Quase todos os exercícios de implementação descrevem uma função ou estrutura de dados sujeita a algumas condições. É da sua responsabilidade testar os casos suficientes para assegurar o comportamento esperado.
A linguagem de programação que usar é indiferente, desde que não dê tiros nos pés com opções aberrantes tipo “C” ou “COBOL”. Ou “JavaScript”. Principalmente “JavaScript”.
Também não é fundamental a maneira como organiza o código, seja em classes ou de outra forma, desde que o organize logicamente.
Mais alguns princípios gerais importantes:
- Os atributos das estruturas devem ter permissões tão restritas quanto possível. Se não for necessário alterar um atributo, não o permita. Se o atributo não tem de ser lido, esconda-o.
- DRY, Don’t Repeat Yourself, Não se repita. Se está a escrever código repetido está a fazer um disparate. Grande. Pare imediatamente e pense como vai evitar as repetições repetições.
- Premature optimization is the root of all evil, A otimização prematura é a raiz de todos os males. O seu código pode ser sempre melhorado: mais rápido, mais geral, mais específico, mais isto e aquilo. Se a melhoria não for necessária não perca tempo com ela.
- Use as ferramentas e adquira os conhecimentos do Engenheiro Informático que vai ser:
- Escolha e use ferramentas com boas comunidades e suporte. Torne-se fluente no seu ambiente de trabalho, na linha de comandos, no editor/ide, a usar repositórios, debuggers, testes, linters, profilers, etc.
- Se ainda não o fez, instale um sistema operativo no seu computador. Infelizmente, em geral, os computadores quando vêm da loja trazem instalada uma coisa que mal serve para utilizadores amadores. Instale e use um sistema operativo baseado em unix, como o linux, o bsd ou o macos.
- Este curso é de Engenharia Informática. Não permita que se confunda com uma qualquer “furmassão avançada de web-bonecos e insta-qualquer-coisa” daquelas que abundam nos motores de pesquisa — basicamente porque GIGO: Garbage In, Garbage Out.
- Invista tempo e esforço a identificar, compreender e resolver as dificuldades. Procure as melhores referências, fale com colegas e com professores — nada com valor é rápido ou fácil.
Os exercícios assinalados com “✓” serão resolvidos nas aulas práticas; Os assinalados com “†” têm elevada dificuldade. Todos os restantes devem ser resolvidos pelos alunos.
Alfabetos, Palavras e Linguagens
Exercício 01
- Defina alfabetos para:
- Escrever os números naturais $0, 1, 2, \ldots$ em notação hexadecimal.
- Representar a configuração de um semáforo, no que diz respeito aos automóveis.
- Escrever as palavras da língua portuguesa.
- Escrever frases em português.
- Seja $\Sigma = \set{0, 1, 2}$ um alfabeto, $u = 012$ e $v = 22021$ palavras sobre $\Sigma$. Escreva por extenso as seguintes palavras:
- $uv$
- $vu$
- $v^R$
- $u^3$
- $012^3$
- $(012)^3$
- $v^0u$
- $(v^2)^R$
Exercício 02
Liste todas as sub-palavras, todos o prefixos e todos os sufixos das seguintes palavras sobre o alfabeto $\Sigma=\set{0, 1, 2, 3}$:
- $01023$
- $11111$
- $\nil$
Exercício 03
Seja $\Sigma = \set{a, b}$. Construa definições recursivas dos seguintes conjuntos:
- $C_1 = \set{\text{palavras sobre } \Sigma \text{ tais que o símbolo } a \text{ ocorre aos pares}}$. $C_1$ inclui, por exemplo, $bbaab$ e $aaaa$ mas não inclui $aaa$ nem $aabaaaba$.
- $C_2 = \set{p \in \cl{\Sigma} \st \len{p} \text{ é par }, p \text{ começa por } a \text{ e, em }p\text{, os } a \text{ e os } b \text{ ocorrem alternados}}$.
- $C_3 = \set{p \in \cl{\Sigma} \st p\ \text{é capicua}}$.
- ✓ $C_4 = \set{a^nb^n \in \cl{\Sigma} \st n > 0}$.
- $C_5 = \set{a^ib^j \in \cl{\Sigma} \st 0 \leq i < j}$.
- ✓ $C_6 = \set{p \in \cl{\Sigma} \st \len{p}_a = \len{p}_b}$. Sugestão: Use a concatenação no passo recursivo.
Exercício 04
Encontre a menor palavra sobre o alfabeto $\Sigma = \set{0}$ que não está em $\set{\nil, 0, 0^2, 0^5}^3$.
Exercício 05
- † Demonstre as propriedades do fecho de linguagens.
- † Demonstre as propriedades da concatenação de expressões regulares.
Exercício 06
Na ordem lexicográfica, quantas palavras estão entre $0$ e $1$? E na ordem mista?
Exercício 07
Desenhe os diagramas das seguintes linguagens:
- $\set{0^n \st n\ \text{é par}}$.
- $\set{p \in \cl{\set{0, 1}} \st \len{p} \leq 4}$.
- $\set{0^n1^n \st n \geq 0}$.
- $\set{0^n1^m \st n, m \geq 0}$.
Exercício 08
Descreva recursivamente o conjunto das palavras sobre o alfabeto $\set{a, b}$…
- com número par de símbolos.
- com número par de ocorrências de $a$.
- com número par de ocorrências de $a$ e número ímpar de ocorrências de $b$.
- com número ímpar de símbolos ou com menos de $n$ símbolos.
- com número ímpar de símbolos ou com, pelo menos, $n$ símbolos.
- com número ímpar de símbolos e com menos de $n$ símbolos.
- com número ímpar de símbolos e com, pelo menos, $n$ símbolos.
- de comprimento menor do que $n$ e com numero par de ocorrências de $b$.
- formadas por um certo número de $a$, seguido de um único $b$, seguido do mesmo número de $a$.
Exercício 09
- Calcule $\set{0, 1}\set{1, 2}$ e compare com $\set{1, 2}\set{0, 1}$. Enuncie o que observou como uma propriedade geral das operações de linguagens.
- É verdade que $\len{AB} = \len{A}\len{B}$?
- Sejam $A = \set{ (01)^n \st n\geq 0}$ e $B = \set{01, 010}$. Calcule $AB$ e $ABA$.
- Verifique que $\cl{\set{0, 10}}$ é a linguagem das palavras binárias que não têm $11$ como subpalavra e que terminam em $0$.
- † Confirme que $A^+ = \cl{A}$ se e só se $\nil \in A$.
- † Confirme que $\del{AB}^R = B^R A^R$ e que $\del{A \cup B}^R = A^R \cup B^R$.
Exercício 10
Mostre que, se $A, B$ forem linguagens então $\clpar{A \cup B} = \cl{A} \clpar{B\cl{A}}$.
Lembre-se que para provar que dois conjuntos $X, Y$ são iguais tem de provar as duas inclusões $X \subseteq Y$ e $Y \subseteq X$.
Exercício 11
Sejam $A = \set{\tt anti, pro, \nil}, B=\set{\tt pesso, soci}, C= \set{\tt al}$. O que são $ABC$ e $\cl{A}BC$?
Exercício 12
† Seja $A$ uma linguagem sobre $\set{0, 1}$ e $p \in \cl{\set{0, 1}}$. Encontre condições necessária e suficientes para que se verifique $\cl{A}\setminus\set{x} = A^+$.
Exercício 13
Verifique, com demonstrações ou contra-exemplos, quais das seguintes igualdades são válidas para todas as linguagens:
- $\clpar{A^R} = \del{\cl{A}}^R$.
- $\clpar{A^+} = \cl{A}$.
- $\clpar{A\cup A^R} = \cl{A} \cup \del{\cl{A}}^R$.
- $A^2 \cup B^2 = \del{A\cup B}^2$.
- $\cl{A} \cap \cl{B} = \clpar{A\cap B}$.
Exercício 14
Mostre que para $n \geq 1$:
- $\bigcup_{i=0}^n A^i = \del{\set{\nil} \cup A}^n$.
- $\del{\cl{A}}^n = \cl{A}$.
- Se $\nil \not\in A$ então $\del{A^+} = A^n \cl{A}$.
Exercício 15
Demonstre as seguintes igualdades:
- $A\clpar{BA} = \clpar{AB}A$.
- $\clpar{A \cup B} = \clpar{\cl{A}\cl{B}}$.
- $A\del{B\cup C} = AB \cup AC$.
- $\del{A \cup B}C =AC \cup BC$.
- $\cl{A}B\clpar{D\cl{A}B\cup C} = \clpar{A \cup B\cl{C}D}B\cl{C}$.
Expressões Regulares
Exercício 16
✓ Considere a expressão regular $\clpar{11 \cup 0}\clpar{00 \cup 1}$ e o respetivo diagrama.
- Encontre uma palavra incompatível com esta expressão regular.
- O que acontece se remover a aresta $\nil$ central do diagrama simplificado?
Exercício 17
- Desenhe e simplifique o diagrama de $\cl{a}b\clpar{c \cup d\cl{a}}$.
- Encontre a mais curta palavra não vazia das linguagens das seguintes expressões:
- $10\cup \del{0 \cup 11}\cl{0}1$.
- $\clpar{00 \cup 11 \cup \del{01 \cup 10}\clpar{00 \cup 11}\del{01 \cup 10}}$.
- $\clpar{\clpar{00 \cup 11} \cup \clpar{001 \cup 110}}$.
- Defina informalmente um algoritmo para encontrar a menor palavra numa linguagem regular definida por:
- Uma expressão regular.
- O diagrama de uma expressão regular.
Exercício 18
-
Desenhe os diagramas das seguintes expressões regulares:
- $\del{00 \cup 10}\clpar{101}\cup 01$.
- $\clpar{\clpar{00 \cup 11} \cup \clpar{001 \cup 110}}$.
- $\clpar{a \cup b\cl{c}d}b\cl{c}$.
-
Determine as expressões regulares definidas pelos seguintes diagramas:
-
Determine o menor diagrama que representa $\nil$.
-
Encontre exemplos que mostram a necessidade de cada uma das condições do teorema da remoção das arestas $\nil$.
Exercício 19
Construa uma expressão regular para representar os números reais sem sinal, de acordo com as seguintes regras:
- Um número real tem sempre uma vírgula decimal.
- Um número real começa por 0 se e só se a sua parte inteira é 0.
- Um número real termina em 0 se e só se a sua parte decimal é 0.
Exercício 20
Encontre expressões regulares para representar as seguintes linguagens:
- ✓ A linguagem das palavras sobre $\set{a,b,c}$ em que todos os $a$’s precedem todos os $b$’s que, por sua vez, precedem todos os $c$’s (donde que todos os $a$’s precedem todos os $c$’s), podendo não haver nem $a$’s, nem $b$’s, nem $c$’s.
- ✓ A linguagem da alínea anterior sem a palavra vazia.
- As palavras sobre $\set{a,b,c}$ de comprimento inferior a 3.
- As palavras sobre $\set{a,b,c}$ que começam por $a$, acabam em $cc$ e têm exatamente dois $b$’s.
- A linguagem das palavras sobre $\set{a,b}$ que têm $aa$ e $bb$ como subpalavras.
- As palavras sobre $\set{a,b}$ de que $bba$ não é subpalavra.
- ✓ A linguagem das palavras sobre $\set{a,b}$ que não têm prefixo $aaa$.
- ✓ A linguagem das palavras sobre $\set{a,b}$ que não têm $aaa$ como subpalavra.
- As palavras sobre $\set{a,b}$ em que $ab$ não ocorre.
- As palavras sobre $\set{a,b}$ em que $ab$ ocorre.
- As palavras sobre $\set{a,b}$ em que $ab$ ocorre só uma vez.
Exercício 21
Descreva informalmente as linguagens representadas pelas seguintes expressões regulares:
- $(a \cup b \cup c)(a \cup b \cup c)\AST $.
- $(a \cup b)((a \cup b)(b \cup a))\AST $.
- $5 \cup (1 \cup 2 \cup \cdots \cup 9)(0 \cup 1 \cup \cdots \cup 9)\AST (0 \cup 5)$.
- $c\AST (a \cup b)(a \cup b \cup c)\AST $.
- $(a(b \cup c)\AST a \cup b \cup c)\AST $.
Exercício 22
Simplifique as seguintes expressões regulares:
- ✓ $\emptyset\AST \cup a\AST \cup b\AST (a \cup b)\AST $
- $aa\AST b \cup b$
- ✓ $b\AST (a \cup (b\AST a\AST )\AST )ab\AST (ab\AST )\AST b$
- † $(a\AST b)\AST \cup (b\AST a)\AST $
Exercício 23
Encontre uma expressão regular para as seguintes linguagens binárias:
- Que representam as potências de $4$.
- Com, pelo menos, uma ocorrência de $001$.
- † Que não têm $001$ como subpalavra.
- Com, quanto muito, uma ocorrência de $00$ e, quanto muito, uma ocorrência de $11$.
- Em que nenhum prefixo tem mais dois $0$s que $1$s nem mais dois $1$s que $0$s.
Exercício 24
Verifique as igualdades $$ \begin{aligned} \cl{0}\clpar{0 \cup 1} &= \clpar{0 \cup \cl{10}} \cr \del{10}^+\del{ \cl{0} \cl{1} \cup \cl{ 0}} &= \clpar{10} \cl{10^+ 1} \end{aligned} $$
Exercício 25
-
Descreva em linguagem natural as linguagens das seguintes expressões regulares:
- $\clpar{ \cl{0} \cl{1}} 0$.
- $\clpar{ \cl{0 1}} 0$.
- $\clpar{00 \cup 11 \cup \del{01 \cup 10}\clpar{00 \cup 11} \del{01 \cup 10}}$.
- $\cl{0} \cup \del{\cl{0} 1 \cup \cl{0} 11}\clpar{0^+ 1 \cup 0^+ 11} \cl{0}$.
-
Simplifique as seguintes expressões regulares:
- $\del{00}\AST 0 \cup \del{00\AST}$.
- $\del{0\cup 1}\del{\nil \cup 00}^+ \cup \del{0 \cup 1}$.
- $\del{0\cup \nil}0\AST 1$.
-
Mostre que $\del{0^2 \cup 0^3}\AST = \del{0^2 0\AST}\AST$.
Exercício 26
Defina expressões regulares para as linguagens binárias das palavras que:
- O quinto símbolo a contar da direita é $0$.
- Têm $000$ ou $111$ como subpalavra.
- Não têm $000$ nem $111$ como subpalavra.
- Não têm $010$ como subpalavra.
- Têm um número ímpar de $0$s.
- Têm um número par de ocorrências de $011$.
Exercício 27
Defina uma ER para as datas de acordo com a Norma ISO 8601. Considere só o caso YYYY-MM-DD:
- Permita que sejam representadas datas incorretas, como
2014-34-96. - Restrinja os valores para os meses e para os dias, mas permita ainda dias inconsistentes com o mês. Por exemplo,
2014-02-31. - Restrinja os valores para os dias de forma a serem consistentes com o mês, mas ignore o anos bissextos (isto é, assuma que fevereiro tem sempre 28 dias). Por exemplo
2004-02-29não é válida. - Trate dos anos bissextos.
Um ano bissexto é um ano múltiplo de 4 (por exemplo, 1948 é bissexto), exceto se também é múltiplo de 100 (por exemplo, 1900 não é bissexto) mas os múltiplos de 400 são sempre bissextos (por exemplo, 1600 é bissexto).
Implementação
Programa 00
Escreva uma função, listWords(fileName) que lê o ficheiro de texto fileName e produz a lista de palavras que ocorrem (sequencialmente) nesse ficheiro. Descarte os símbolos de pontuação e converta as letras para minúsculas. Sugestão: consulte a documentação de str e de string do python.
Programa 01
Escreva uma função, symbolsIn(word), que tem como entrada uma string e que devolve uma lista de símbolos. Assuma que, por omissão, os símbolos da string são separados por underscore (_) mas, opcionalmente, a função tem o argumento sep para usar um separador alternativo.
| Entrada | Resultado |
|---|---|
"a_b_color_b_a" | ["a", "b", "color", "b", "a"] |
"single" | ["single"] |
"" | [""] |
"_" | ["", ""] |
Programa 02
Escreva uma função, alphabetFor(word), que tem como argumento uma string e que devolve o menor alfabeto para gerar essa palavra. Assuma que, por omissão, os símbolos da string são separados por underscore (_) mas, opcionalmente, a função tem o argumento sep para usar um separador alternativo.
Note bem que no resultado não devem aparecer elementos repetidos.
| Entrada | Resultado (sep="_") | Resultado (sep="") |
|---|---|---|
"a_b_color_b_a" | ["a", "b", "color"] | ["a", "_", "b", "c", "o", "l", "r"] |
"single" | ["single"] | ["s", "i", "g", "l", "e"] |
"" | [] | [] |
"_" | [] | ["_"] |
Programa 03
Escreva uma função, generated(word, alphabet), em que word é uma string e alphabet uma lista de string e que determina se os símbolos de word estão todos em word (isto é, o resultado é booleano). Assuma que, por omissão, os símbolos da string são separados por underscore (_) mas, opcionalmente, a função tem o argumento sep para usar um separador alternativo.
Entrada word | Entrada alphabet | Resultado |
|---|---|---|
"a_b_color_b_a" | ["a", "b", "color"] | true |
"single" | ["single"] | true |
"" | [] | true |
Programa 04
Use uma biblioteca de expressões regulares (do python3, por exemplo) e escreva expressões para reconhecer palavras que:
- Começam pela letra
a; Não começam pela letraa; Terminam na letraa; Não terminam na letraa. - Têm pelo menos uma ocorrência de
a; Não têm ocorrências dea; O número de ocorrências deanão é 1; O número de ocorrências deaé exatamente 1. - Têm um
aou umb; Têm umae umb; Têm umae, mais à frente, umb. - Se têm um
aentão também têm umb; Se têm umaentão também têm umbque ocorre antes doa; Se têm umaentão também têm umbque ocorre depois doa; Se têm umaentão não têm umb.
O pressuposto geral nas bibliotecas de ER é que vai ser feita uma pesquisa de subpalavras. Isto é, a ER é usada como um padrão que vai “percorrer” uma palavra “maior” para detetar subpalavras compatíveis com a ER dada.
Não é esse o pressuposto neste capítulo, onde as ER definem “palavras inteiras”.
Programa 05
- Escreva uma função
countRE(expr, words)em queexpré uma das funções acima ewordsuma lista destringe que devolve o número de palavras emwordsaceites pela ER deexpr. - Repita este exercício para a função
filterRE(expr, words)que devolve a lista das palavras emwordsaceites porexpr. Re-escrevacountRE = len(filterRE). - Escreva o predicado
allRE(expr, words)para testar se todas as palavras dewordssão aceites porexpr. O mesmo paraanyRE(expr, words)para testar se alguma palavra é aceite.
Programa 06
- Use os comandos
greppara substituir a funçãofilteracima ewcpara substituirlen. - Aplique os filtros e contagens às palavras portuguesas com as ER dos exercícios anteriores.
- Quantas palavras têm
caldepois de umvsem que ocorra umono meio? Quais estão em comum combritish_english?
Na linha de comandos, em geral, tem a seguinte documentação sobre cada comando, aqui ilustrado com
grep:
grep -hougrep --help, um resumo curto das principais operações.man grep, uma “página” com uma descrição curta do comando e uma lista das operações (a.k.a cheat sheet).info grep, um “livro” com a descrição completa do comando e operações.
Programa 07
Se observar as contagens de palavras portuguesas (no ficheiro portuguese):
- Há 431114 palavras.
- Das quais 355762 com a letra
a - E 75352 em que
anão ocorre.
Use o grep e o wc para obter exatamente estes três números.
Autómatos Finitos
 |
No capítulo anterior definiram-se as linguagens e expressões regulares com vista a resolver o Problema Principal de ALP (versão 1) – Determinar um sistema computável, eficiente e adequado para definir linguagens de programação. – onde:
- Computável: Existe um algoritmo que recebe como entrada uma palavra $p$ e ao fim de um número finito de passos produz uma resposta
simounãoconforme $p \in A$ ou não. - Eficiente: O número de passos referido no passo anterior não deve ser “muito maior” que o comprimento da palavra.
- Adequado: Deve ser possível definir (os programas de) qualquer linguagem de programação.
As linguagens regulares são uma classe de linguagens formais. Será que resolvem o Problema Principal de ALP? É necessário esclarecer:
- Como definir um algoritmo,
Super, que dada uma EReproduza um programaPL = Super(e)tal que, para cada palavrap, o resultadoPL(p)ésimounãoconformep in L(e)ou não? - Se as computações
Super(e)ePL(p)são eficientes? - Se as linguagens regulares são adequadas para definir (os programs de) qualquer linguagem de programação?
O programa
Supertem como entrada uma ERe, que especifica uma certa linguagem regular, e devolve um programaPL, que reconhece as palavras da linguagem definida pore.Isto é semelhante ao trabalho de um compilador. Por exemplo,
javacé um programa que tem como entrada ficheiros que especificam um certo programa e devolve esse programa em bytecode.
Autómatos Finitos Deterministas
Um modelo computacional simples, com memória limitada.
Introdução
| Exemplo de um Autómato Finito |
|---|
 |
| O que acontece quando a entrada é $a\AST$? |
Para resolver o Problema Principal de ALP é necessário formalizar a noção de “computador/programa”, de forma a representar
PL = Super(e).
Os Autómatos Finitos são modelos formais de “computadores/programas” simples de descrever mas capazes de resolver vários problemas teóricos e com algumas aplicações práticas (ver o artigo na wikipedia).
Um autómato tem como entrada uma palavra que é processada símbolo a símbolo até que termina num certo estado. Em certos estados do autómato a palavra, depois de completamente “lida”, é aceite e noutros é rejeitada.
Um autómato pode ser representado por um grafo orientado. Os vértices “são” os estados do autómato e as “arestas” indicam como são “lidos” os símbolos.
Autómato Finito Determinista
Autómato Finito Determinista (AFD). Um Autómato Finito Determinista (AFD) ou Autómato de Estados Finitos (Em inglês: Determinist Finite State Machine (DFSM) ou Determinist Finite State Automaton (DFSA)) é um tuplo $\del{Q, \Sigma, \delta, q_I, F}$ onde:
- Estados de Controlo $Q$ é um conjunto finito.
- Alfabeto de Entrada $\Sigma$ é um alfabeto.
- Transição $\delta: Q \times \Sigma \to Q$ é uma função.
- Estado Inicial $q_I \in Q$.
- Estados Finais ou de Aceitação $F \subseteq Q$.
Intuitivamente, um AFD “anda” de estado em estado, conforme “processa” os símbolos de uma palavra, de acordo com a transição. Esse “passeio” começa no estado inicial e “consome” um símbolo da palavra de cada vez. Quando todos os símbolos estão processados, o AFD fica num certo estado. Se for um dos estados finais a palavra é aceite, caso contrário é rejeitada.
Por exemplo, seja $A = \del{\set{q_0, q_1, q_2, q_3}, \set{0, 1}, \delta, q_0, \set{q_1, q_2}}$ em que a transição $\delta$ é definida pela seguinte tabela: $$ \begin{array}{c|cc} \delta & 0 & 1 \cr \hline q_0 & q_1 & q_2 \cr q_1 & q_2 & q_3 \cr q_2 & q_2 & q_2 \cr q_3 & q_3 & q_3 \end{array} $$
- Os estados de controlo são os elementos de $Q = \set{q_0, q_1, q_2, q_3}$.
- O alfabeto de entrada é $\Sigma = \set{0, 1}$.
- A transição é a função $\delta(q,s) = q’$ em que $q’$ está na linha $q$ e coluna $s$ da tabela acima.
- O estado inicial é $q_I = q_0$.
- Os estados finais são os elementos de $F = \set{q_1, q_2}$.
A função de transição de um AFD é quase sempre representada por uma tabela como no exemplo acima. Mas por vezes é conveniente apresentá-la como um conjunto de triplos: $$\set{\del{i, a, j} \st j = \delta\at{i, a}, i \in Q, a \in \Sigma}.$$
A transição acima como um conjunto de triplos fica: $$\set{\del{q_0, 0, q_1}, \del{q_0, 1, q_2}, \del{q_1, 0, q_2}, \del{q_1, 1, q_3}, \ldots}$$
Configuração, Computação, Aceitação
A computação da palavra $p = 000$ por este autómato é a sequência $$q_0 \trf{0} q_1 \trf{0} q_2 \trf{0} q_2 \in F.$$
A notação $q \trf{a} q’$ indica que o autómato passa do estado $q$ para $q’$ lendo o símbolo $a$. Concatenado todos esses símbolos, da esquerda para a direita, obtém-se a palavra processada, neste caso $p = 000$. Também é indicado que o último estado é final, pelo que a palavra $p$ é aceite pelo autómato $A$.
Configuração. Computação. Palavra Aceite. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFD.
Uma configuração de $A$ é um par $\del{q, s}\in Q \times \cl{\Sigma}$ onde $q$ é o estado atual e $s$ é o sufixo restante.
A computação da palavra $p = a_1 a_2 \ldots a_n \in \cl{\Sigma}$ pelo AFD $A$ é a sequência de configurações $$\del{q_0, a_1 a_2 \ldots a_n} \vdash_A \del{q_1, a_2 \ldots a_n} \vdash_A \cdots \vdash_A \del{q_n, \nil}$$ em que:
- base (configuração inicial) $q_0 = q_I$.
- passo (processamento do símbolo ativo) $q_i = \delta\del{q_{i-1}, a_i}, i \geq 1$.
Se $q_n\in F$ a palavra $p$ é aceite pelo autómato $A$. Caso contrário, $p$ é rejeitada por $A$.
Por exemplo, aplicando estas definições ao autómato anterior:
- De acordo com a base, a configuração inicial é $\del{q_0, \underline{0}00}$. O “símbolo ativo” está sublinhado.
- Aplicando o passo obtém-se a configuração $\del{q_1, \underline{0}0}$ porque $q_1 = \delta\del{q_0, 0}$.
- O passo é repetidamente aplicado, consumindo o símbolo ativo de cada vez, até que o sufixo restante é $\nil$:
- $\del{q_1, \underline{0}0} \vdash \del{q_2, \underline{0}}$.
- $\del{q_2, \underline{0}} \vdash \del{q_2, \nil}$.
A computação pode ser visualizada numa tabela, com uma configuração por linha
$$ \begin{array}{c|l} q & s \cr \hline q_0 & 000 \cr q_1 & 00 \cr q_2 & 0 \cr q_2 & \nil \end{array} $$ ou de forma ainda mais compacta: $$ \begin{array}{l} q_0 000 \cr q_1 00 \cr q_2 0 \cr q_2 \nil \end{array} $$ ou ainda $$ q_0 \trf{000} q_1 \trf{00} q_2 \trf{0} q_2 \in F. $$
A computação termina quando não é possível fazer mais transições. Neste exemplo o autómato fica no estado $q_2 \in F$. Portanto $p = 000$ é aceite por $A$.
O que acontece com $p=010$? A computação é a sequência: $$ q_0 \trf{010} q_1 \trf{10} q_3 \trf{0} q_3 \not\in F. $$
Neste caso a computação termina no estado $q_3 \not\in F$. Portanto $010$ é rejeitada por $A$.
Diagramas dos Autómatos Finitos Deterministas
Tal como com as expressões regulares, a visualização gráfica dos autómatos finitos deterministas é uma ferramenta útil.
Diagrama de um AFD. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFD. O diagrama de $A$ é um grafo orientado em que:
- Os vértices são os estados de controlo $q\in Q$.
- Os arcos são definidos pela transição. Se $q’ = \delta\del{q, a}$ então o diagrama tem o arco
- O (único) vértice com o estado inicial é assinalado por um arco órfã a entrar:
- Os (vários) vértices com estados finais são assinalados por um círculo duplo:
Por exemplo, o AFD usado nos exemplos acima tem o seguinte diagrama:
| Diagrama de um AFD |
|---|
 |
Transição Estendida
A transição de um AFD está definida para cada símbolo do alfabeto de entrada: $\delta: Q \times \Sigma \to Q$. No entanto é mais conveniente estender as transições a palavras: $\hat{\delta}: Q \times \cl{\Sigma} \to Q$.
Transição Estendida. Seja $A=\del{Q, \Sigma, \delta, q_I, F}$ um AFD. A função de transição estendida tem assinatura $\hat{\delta}: Q \times \alert{\cl{\Sigma}} \to Q$ e fica definida pelas seguintes regras recursivas:
- base - palavra vazia $\hat{\delta}\del{q, \nil} = q$.
- base - símbolos Para cada $a \in \Sigma, \hat{\delta}\del{q, a} = \delta\del{q, a}$.
- passo Se $p\in\cl{\Sigma}, a \in\Sigma$ então $\hat{\delta}\del{q, pa} = \delta\del{\hat{\delta}\del{q, p}, a}$.
Intuitivamente, $\hat{\delta}\del{q, p}$ é o estado em que o AFD fica depois de processar a palavra $p$ a partir do estado $q$.
Por exemplo, usando o AFD anterior: $$ \begin{aligned} \hat{\delta}\del{q_0, 000} &= \delta\del{\hat{\delta}\del{q_0, 00}, 0} \cr &= \delta\del{\delta\del{\hat{\delta}\del{q_0, 0}, 0}, 0} \cr &= \delta\del{\delta\del{\delta\del{q_0, 0}, 0}, 0} \cr &= \delta\del{\delta\del{q_1, 0}, 0} \cr &= \delta\del{q_2, 0} \cr &= q_2 \end{aligned} $$ e $$ \begin{aligned} \hat{\delta}\del{q_0, 010} &= \delta\del{\hat{\delta}\del{q_0, 01}, 0} \cr &= \delta\del{\delta\del{\hat{\delta}\del{q_0, 0}, 1}, 0} \cr &= \delta\del{\delta\del{\delta\del{q_0, 0}, 1}, 0} \cr &= \delta\del{\delta\del{q_1, 1}, 0} \cr &= \delta\del{q_3, 0} \cr &= q_3 \end{aligned} $$
Com transições estendidas a escrita de certas definições e condições fica mais compacta e intuitiva:
- Computação $\hat{\delta}\del{q, p} = q’ \Leftrightarrow \del{q, p} \alert{\vdash_A^{\ast}} \del{q’, \nil}$.
- Aceitação $p\in\cl{\Sigma}$ é aceite pelo AFD $A$ se, e só se $\hat{\delta}\del{q_I, p}\in F$. Se $\hat{\delta}\del{q_I, p} \not\in F$ então $p$ é rejeitada.
Linguagens Reconhecidas pelos AFD
É altura de começar a fazer a ligação entre as linguagens regulares e os AFD.
Linguagem Reconhecida por um AFD. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFD.
A linguagem reconhecida (ou aceite) por $A$ é $$L\at{A} = \set{p \in \cl{\Sigma}\st \hat{\delta}\at{q_I, p} \in F}.$$
Dois AFD são equivalentes se aceitam a mesma linguagem.
Tal como com as expressões regulares, a definição de “equivalência” depende das linguagens associadas.
Conclusão
Nesta secção definiu-se um modelo de “computação” simples, os autómatos finitos deterministas e associou-se uma linguagem a cada AFD.
A intenção aqui é obter-se um modelo de computação das linguagens regulares. Portanto é preciso responder afirmativamente a estas duas questões:
- Qualquer linguagem regular é aceite por um AFD?
- Qualquer linguagem aceite por um AFD é regular?
Estas duas questões são tratadas na próxima secção.
Computação Não Determinista
Generalização dos autómatos deterministas.
Introdução
Com vista a obter-se um modelo de computação das linguagens regulares, estão por responder duas questões:
- Qualquer linguagem regular é aceite por um AFD?
- Qualquer linguagem aceite por um AFD é regular?
Formalmente, para responder a estas questões, mostra-se como obter um AFD “equivalente” a uma ER dada e, reciprocamente, como obter uma RE “equivalente” a um dado AFD.
Para construir estas equivalências é necessária estudar uma variante não determinista dos AFD.
Autómatos Finitos Não Deterministas
Nos AF deterministas há sempre exatamente uma transição para cada combinação $(q,a) \in Q \times \Sigma$. Isto é, no diagrama, de cada estado $q$ sai sempre exatamente uma aresta $a$, para cada $a \in \Sigma$.
| Diagrama de Um AFD. |
|---|
 |
| De cada vértice sai exatamente uma aresta para cada símbolo. |
Para os diagramas das expressões regulares o caso é diferente:
- Algumas arestas “são” $\nil$.
- Não é necessário sair uma aresta para cada símbolo.
- Podem sair várias arestas com o mesmo símbolo.
Por exemplo, para a expressão regular $\clpar{11 \cup 0}\clpar{00 \cup 1}$ tem-se o diagrama
| Diagrama de uma ER. |
|---|
 |
| Não se verificam as restrições dos AFD. |
Intuitivamente, as arestas dos AFD são caminhos obrigatórios enquanto que as arestas das RE são caminhos possíveis.
Os Autómatos Finitos Não Deterministas generalizam os AFD com todos os tipos de arestas das ER. Desta forma obtém-se um modelo computacional das ER que pode “correr” e ser analisado em termos de desempenho.
Autómato Finito Não Determinista (AFND). Um Autómato Finito Não Determinista (AFND) é um tuplo $A = \del{Q, \Sigma, \delta, q_I, F}$ em que
- Estados de Controlo $Q$ é um conjunto finito.
- Alfabeto de Entrada $\Sigma$ é um alfabeto.
- Transição $\alert{\delta: Q \times \del{\Sigma \cup \set{\nil}} \to \mathcal{P}\at{Q}}$ é uma função.
- Estado Inicial $q_I \in Q$.
- Estados Finais ou de Aceitação $F \subseteq Q$.
A diferença entre as definições de AFD e AFND está na assinatura da transição:
- A assinatura da transição dos AFD é $\delta: Q \times \Sigma \to Q$.
- Nos AFND acrescenta-se a palavra vazia $\nil$ a $\Sigma$. Desta forma, nos diagramas algumas arestas também podem ser $\nil$, além de $a\in\Sigma$.
- Em vez de $\delta\del{q, x}$ ser um único estado de controlo, nos AFND é um conjunto de possíveis estados, incluindo nenhum. Isto é, em vez de $\alert{\delta\del{q, x} \in Q}$, nos AFND $\alert{\delta\del{q, x}\subseteq Q}$.
É necessário replicar nos AFND o percurso feito com os AFD. Em particular, definir para os AFND o que é uma configuração, computação, palavra e linguagem aceite. Porém, é mais útil começar por definir o diagrama de um AFND.
Diagrama de um AFND. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFND. O diagrama de $A$ define-se como no caso dos AFD, tendo em conta que algumas arestas podem ser $\nil$.
Por exemplo, dado o AFND com estado inicial $q_I = 0$, estados finais $F=\set{2}$ e transição $$ \begin{array}{c|ccc} q & 0 & 1 & \nil \cr \hline 0 & \empty & \set{0,\ 1} & \set{1} \cr 1 & \set{2} & \set{1,\ 2} & \empty \cr 2 & \set{2} & \empty & \set{1} \end{array} $$ o diagrama que se obtém é
| Exemplo de Diagrama de um AFND |
|---|
 |
Note-se que:
- A tabela da transição tem uma coluna adicional, $\nil$.
- As “células” da tabela são subconjuntos de estados de controlo. Um valor possível é o conjunto vazio $\empty$.
- Neste primeiro exemplo os conjuntos foram denotados com $\set{\ldots}$ mas sempre que possível será usada uma notação mais compacta:
- Em vez de se escrever “$\set{0,\ 2}$” escreve-se apenas “$02$”, “$0\ 2$” ou “$0,2$” se a vírgula for mesmo necessária.
- O conjunto vazio é representado por nada: em vez de “$\empty$” escreve-se apenas “”.
- Os estados finais podem ser assinalados com o prefixo “$f$” e o estado inicial com um prefixo “$i$”. Se nada for indicado o estado inicial é sempre $q_0$ ou $0$ e dispensa-se a indicação de que é inicial.
De acordo com estas convenções a tabela da transição acima fica $$ \begin{array}{r|c|c|c} & 0 & 1 & \nil \cr \hline 0 & & 0\ 1 & 1 \cr 1 & 2 & 1\ 2 & \cr f2 & 2 & & 1 \end{array} $$ e define completamente o AFND $A$. Isto é, lendo a tabela determinam-se $Q, \Sigma, \delta, q_I, F$ todos os atributos que definem um AFND.
Tal como observado para os AFD, a função de transição de um AFND é quase sempre representada por uma tabela mas por vezes é conveniente apresentá-la como um conjunto de triplos: $$\set{\del{i, a, J} \st J = \delta\at{i, a}}.$$
A transição acima, como um conjunto de triplos, fica: $$\set{\del{0, 0, \empty}, \del{0, 1, \set{0, 1}}, \del{0, \nil, \set{1}}, \del{1, 0, \set{2}}, \del{1, 1, \set{1, 2}}, \del{1, \nil, \empty}, \ldots}$$
Observação: No caso dos AFD os triplos são $\del{i, a, j} \in Q \times \Sigma \times \alert{Q}$ e para os AFND os triplos são $\del{i, a, J} \in Q \times \Sigma \times \alert{\mathcal{P}\at{Q}}$. Enquanto que nos AFD $j \in Q$, nos AFND $J \subseteq Q$, podendo $J$ ser vazio, ter zero, um, dois, $n$ elementos de $Q$.
Configuração. Computação AFND. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFND.
A definição de configuração como um par $\del{q, s} \in Q \times \cl{\Sigma}$ permanece igual ao caso dos AFD.
A computação da palavra $p = a_1 a_2 \ldots a_n \in \cl{\Sigma}$ pelo AFND $A$ é uma sequência de configurações $$\del{q_0, p_0} \vdash_A \del{q_1, p_1} \vdash_A \cdots \vdash_A \del{q_n, p_n}$$ em que:
- base (configuração inicial) $q_0 = q_I$ e $p_0 = p$.
- passo (processamento do símbolo ativo): $q_{i+1}\ \alert{\in}\ \delta\del{q_i, a}$ e $p_i = ap_{i+1}$.
- passo (transição vazia): $q_{i+1}\ \alert{\in}\ \delta\del{q_i, \alert{\nil}}$ e $p_i = p_{i+1}$.
- fim $p_n = \nil$ ou não há mais passos possíveis.
Ao contrário do que acontece com os AFD, nos AFND cada palavra pode ter mais do que uma computação possível.
Por exemplo, a palavra $01$ tem três computações possíveis:
- $0 \trf{\nil} 1 \trf{0} 2 \trf{\nil} 1 \trf{1} 1 \not\in F$: rejeita?
- $0 \trf{\nil} 1 \trf{0} 2 \trf{\nil} 1 \trf{1} 2 \in F$: aceita?
- $0 \trf{\nil} 1 \trf{0} 2 \trf{\nil} 1 \trf{1} 2 \trf{\nil} 1 \not\in F$: rejeita?
Esta situação, em que as computações de uma palavra podem terminar em vários estados, alguns finais e outros não, torna a definição de palavra aceite um pouco mais complicada do que para os AFD:
Palavra Aceite. Linguagem Reconhecida (AFND). Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFND.
Uma palavra $p\in \cl{\Sigma}$ é aceite por $A$ se existe alguma computação de $p$ por $A$ que termina num estado final $q \in F$ depois de terem sido lidos todos os símbolos de $p$. Isto é, se entre todas as computações de $p$ por $A$ alguma termina numa configuração $\del{q, \nil}$ com $q\in F$.
A linguagem reconhecida (ou aceite) por $A$ é o conjunto de todas as palavras aceites por $A$: $$L(A) = \set{p : \exists \del{q_I, p} \vdash_A^{\ast} \del{q, \nil}, q \in F}$$
Neste ponto a situação em relação ao Problema Principal de ALP é a seguinte :
- As Linguagens e as Expressões Regulares são candidatas para formalizar rigorosamente as linguagens de programação. Idealmente, cada linguagem de programação poderia ser representada por uma ER.
- Os Autómatos Finitos Deterministas são candidatos para resolver computacionalmente a questão de saber se um palavra dada está, ou não, numa certa linguagem regular.
- Mas os AFD parecem ser demasiado restritivos para representar as ER. Comparando os respetivos diagramas, não há arestas vazias, etc.
- Os Autómatos Finitos Não Deterministas generalizam os AFD de forma a suportarem todos os tipos de arestas das ER.
De forma a resolver a questão da representação computacional das linguagens regulares, há que responder afirmativamente às seguintes duas questões;
- Qualquer linguagem regular é aceite por um AFND?
- Qualquer linguagem aceite por um AFND é regular?
Equivalência entre Expressões Regulares e Autómatos Finitos Não Deterministas
Para estabelecer a equivalência entre ER e AFND têm de ser resolvidos dois problemas:
- ER → AFND (Construção de Thompson): Dada uma ER qualquer, $e$, encontrar um AFND $A$ tal que $L(A) = L(e)$ (isto é, Qualquer linguagem regular é aceite por um AFND?).
- AFND → ER (Algoritmo de Kleene): Dado um AFND qualquer, $A$, encontrar uma ER $e$ tal que $L(e) = L(A)$ (isto é, Qualquer linguagem aceite por um AFND é regular?).
A resolução do primeiro problema usa a “Construção de Thompson” descrita já a seguir. Para resolver o segundo problema usa-se o “Algoritmo de Kleene”, que remove um a um os vértices do diagrama do AFND.
Construção de Thompson
O primeiro problema é de resolução muito fácil, considerando os diagramas das ER e dos AFND:
Construção de Thompson. Dada uma ER $e$ sobre $\Sigma$, o diagrama de $e$ pode ser interpretado como o diagrama de um AFND $A$. Nesse caso $L(A) = L(e)$.
Por exemplo, seja $e = a \cup b\clpar{a \cup b}$. Numerando os vértices do seu diagrama da esquerda para a direita (mas serve qualquer critério desde que cada vértice fique com um “nome” diferente dos restantes) obtém-se:
| Exemplo de um Diagrama da ER $a \cup b\clpar{a \cup b}$ |
|---|
 |
Seja $A$ o AFND que se obtém deste diagrama, descrito pela tabela
$$ \begin{array}{r|c|c|c} & a & b & \nil \cr \hline 0 & 3 & 1 \cr 1 & & & 2 \cr 2 & 2 & 2 & 3 \cr f3 \end{array} $$
A “equivalência” entre $e$ e $A$ depende de se verificarem as seguintes duas condições:
- $L(e) \subseteq L(A)$: Cada palavra de $L(e)$ é aceite por $A$ ou, equivalentemente, $\overline{L(A)} \subseteq \overline{L(e)}$: cada palavra rejeitada por $A$ não está em $L(e)$.
- $L(A) \subseteq L(e)$: Cada palavra aceite por $A$ está em $L(e)$ ou, equivalentemente, $\overline{L(e)} \subseteq \overline{L(A)}$: cada palavra que não está em $L(e)$ é rejeitada por $A$.
A demonstração completa e formal de cada um dos pontos anteriores sai do âmbito de ALP. Mas a verificação de alguns casos é um exercício importante.
- Palavras de $L(e)$: $a, b, ba, baba$. Estas palavras são aceites por $A$?
- Palavras que não estão em $L(e)$: $\nil, aa, ab$. Estas palavras são rejeitadas por $A$?
Para verificar que a palavra $p$ é aceite por $A$, basta que uma computação de $p$ por $A$ processe todos os símbolos $p$ e termine num estado final.
Por exemplo, $p = a$ tem a seguinte computação por $A$: $0 \trf{a} 3\in F$. Portanto $p = a$ é aceite por $A$.
Para $p = b$ há a seguinte computação: $0 \trf{b} 1 \trf{\nil} 2 \trf{\nil} 3 \in F$. Todos os símbolos de $p = b$ foram processados e a computação termina num estado final. Portanto $p = b$ é aceite.
Exercício. Verifique que as restantes palavras de $L(e)$ listadas acima também são aceites por $A$.
Para verificar que a palavra $p$ é rejeitada por $A$ é necessário que nenhuma computação de $p$ por $A$ processe todos os símbolos $p$ e termine num estado final.
Por exemplo, $p=\nil$ tem apenas uma computação por $A$: $0 \not\in F$ (começa no estado inicial e não avança mais).
Embora esta computação processe todos os símbolos de $p=\nil$, não termina num estado final. Como não há mais computações de $p = \nil$ por $A$ conclui-se que $A$ rejeita $p=\nil$.
Se $p = aa$ também só há uma computação possível: $0\trf{a} 3 \in F$ e daqui não é possível avançar mais. Neste caso, embora a computação tenha terminado num estado final, faltou processar todos os símbolos de $p = aa$. Portanto esta palavra é rejeitada.
Exercício. Verifique que as restantes palavras listadas acima que não estão em $L(e)$ também são rejeitadas por $A$.
Algoritmo de Kleene
Com a Construção de Thompson fica estabelecido que qualquer linguagem regular é aceite por um AFND. Falta verificar que qualquer linguagem aceite por um AFND é regular.
Para esse efeito apresenta-se um método, o “Algoritmo de Kleene”, que transforma o diagrama de um AFND numa expressão regular “equivalente”.
Neste processo o diagrama é transformado por uma sequência de passos onde se remove um vértice de cada vez. O vértice removido é substituído por certas ER. No fim do processo fica apenas o vértice inicial e um vértice final, ligados por uma aresta com a ER final.
Um exemplo, ainda informal
-
Dado o seguinte AFND na forma de um diagrama:
-
Representa-se por $E_{ij}$ a expressão da aresta que liga o vértice $i$ ao vértice $j$. Por exemplo, $E_{12} = a, E_{23} = \nil$.
-
Neste diagrama:
- Nenhuma aresta entra no vértice inicial.
- Existe apenas um vértice final.
- Nenhuma aresta sai do vértice final.
-
Para eliminar o vértice $1$:
- Que caminhos “passam em $1$”? Há dois: $0 \to 1 \to 2$ e $2 \to 1 \to 2$.
- Seja $i \to k \to j$ um desses caminhos. Adiciona-se ao diagrama a aresta $i \to j$ com $E_{ij} \cup E_{ik} \clpar{E_{kk}} E_{kj}$.
- Repete-se o passo anterior para todos os caminhos que passam no vértice a eliminar.
-
O novo diagrama, sem o vértice $1$, é:
-
Eliminado o vértice $2$, obtém-se:
-
Restam apenas o vértice inicial e o final. A expressão regular “equivalente” ao AFND é $a\clpar{ba}$.
O núcleo do processo está no passo 4 mas antes de começar é preciso que o diagrama do AFND esteja “bem preparado”, conforme as condições do passo 3.
Diagrama Bem Preparado. Um diagrama está bem preparado se
- Nenhuma aresta entra no vértice inicial.
- Existe apenas um vértice final.
- Nenhuma aresta sai do vértice final.
Nem todos os diagramas estão bem preparados mas é sempre possível transformar um diagrama de forma a obter-se outro equivalente e bem preparado:
Autómato Bem Preparado. Seja $A=\del{Q, \Sigma, \delta, q_I, F}$ um AFND.
O AFND $A’ = \del{Q\cup \set{q’_I, q_f}, \Sigma, \delta’, q’_I, \set{q_F}}$ em que:
- $q’_I \not= q_F$ e $\set{q’_I, q_F}\cap Q = \empty$.
- $\delta’\at{q’_I, \nil} = \set{q_I}$.
- $\delta’\at{q, \nil} = \set{q_F}$ para cada $q \in F$.
- $\delta’\at{q, x} = \delta\at{q, x}$ nos restantes casos.
está bem preparado e é equivalente a $A$.
Por exemplo, se $A$ for dado pela tabela $$ \begin{array}{r|c|c|c} \delta & a & b & \nil \cr \hline 0 & 1 \cr f1 & & 0 \cr \end{array} $$ não está bem preparado porque o estado inicial, $0$, recebe uma aresta de $1$ e, também, porque sai uma aresta do estado final. Um AFND equivalente e bem preparado é $$ \begin{array}{r|c|c|c} \delta’ & a & b & \nil \cr \hline iq’_I &&&0\cr 0 & 1 \cr 1 & & 0 & q_F \cr fq_F & \end{array} $$ que está bem preparado. Em termos de diagramas:
| Diagrama Mal Preparado | Diagrama Equivalente Bem Preparado |
|---|---|
 |  |
Com autómatos bem preparados pode aplicar-se o processo de eliminação de vértices.
Algoritmo de Kleene. Sejam $A$ um AFND bem preparado e $E_{ij}$ a ER da aresta $i\to j$ no diagrama de $A$.
O caminho $i \to k \to j$ passa no vértice $k$ se $i,j \not= k$ (pode ser $i = j$) e no diagrama existem arestas $i \to k$ e $k \to j$.
A eliminação do vértice $k$ produz um novo diagrama idêntico ao anterior exceto:
- O novo diagrama não tem o vértice $k$.
- Para cada caminho $i \to k \to j$ do diagrama original, o novo diagrama tem a aresta $i \to j$ com valor
$$E_{ij} \cup E_{ik}\clpar{E_{kk}}E_{kj}.$$
No diagrama que se obtém quando foram eliminados todos os vértices exceto o inicial e final, a expressão regular $E_{IF}$ que está na aresta $q’_I \to q_F$ é “equivalente” ao AFND $A$ no sentido em que $$ L\at{E_{IF}} = L\at{A}.$$
Um exemplo mais complicado, passo a passo. Seja $A$ o seguinte diagrama/AFND, que não está bem preparado:
Uma versão equivalente, bem preparada é
Eliminar $0$. Caminhos que passam em $0$:
- $I \to 0 \to 1$. ER resultante: $\nil \cup a$.
- $I \to 0 \to 2$. ER resultante: $b$.
Eliminar $2$. Caminhos que passam em $2$:
- $I \to 2 \to 3$. ER resultante: $b$.
- $3 \to 2 \to 3$. ER resultante: $a \cup b$.
Eliminar $3$. Caminhos que passam em $3$:
- $I \to 3 \to 1$. ER resultante: $\nil \cup a \cup b\clpar{a \cup b} a$.
- $1 \to 3 \to 1$. ER resultante: $b \cup b\clpar{a \cup b}a$.
Eliminar $1$. Caminhos que passam em $1$:
- $I \to 1 \to F$. ER resultante, e final: $$x = \del{\nil \cup a \cup b\clpar{a \cup b} a} \clpar{b \cup b\clpar{a \cup b}a}.$$
A ER final pode ser um pouco simplificada: $$x = \del{\nil \cup a} \clpar{b \cup b\clpar{a \cup b}a}.$$
Exercícios:
- Aplique a Construção de Thompson à ER $x$ acima.
- Escolha palavras de $L(x)$ e verifique que $A$ as aceita.
- Encontre palavras de $L(A)$ e verifique que estão em $L(x)$.
- O que se passa com a palavra $aa$? Está em $L(x)$? E em $L(A)$?
Equivalência entre AFND e AFD
A Construção de Thompson e o Algoritmo de Kleene asseguram que os AFND são “equivalentes” às ER, no sentido em que os AFND e as ER definem exatamente as mesmas linguagens.
Mas os AFND são um mau modelo computacional porque pode ser necessário um número exponencial (no número de estados do autómato) para decidir se $p \in L\at{A}$.
Para computar $p \in L(A)$ não se sabe, à partida, quantos “passos” vão ser necessários. No caso em que $p \not\in L(A)$ é preciso testar todas computações de $p$ por $A$.
O problema da eficiência da computação não se coloca nos AFD: Demora sempre exatamente $\len{p}$ passos, o que é um desempenho ótimo (no sentido em que não há melhor).
Como os AFND generalizam os AFD, todas as linguagens aceites por AFD são também aceites por AFND.
Nesta secção mostra-se que os AFD e os AFND são equivalentes: As linguagens aceites pelos AFD são exatamente as linguagens aceites pelos AFND.
Com as transições vazias, um AFND pode percorrer vários estados sem processar símbolos, ao contrário do que acontece com os AFD. Esta situação fica representada com o fecho vazio e com a transição de entrada.
Fecho Vazio. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFND e $q\in Q$.
O fecho vazio de $q$, $\ecl\at{q}$, é o conjunto de todos os estados que podem ser alcançados a partir de $q$ com zero ou mais transições vazias. Formalmente:
- base $q\in\ecl\at{q}$.
- passo Se $p \in \ecl\at{q}$ e $p’ \in \delta\at{p, \nil}$ então também $p’ \in \ecl\at{q}$.
Também devido às transições vazias, $\delta\at{q,a}$ não contém todos os estados que podem ser alcançados a partir de $q$ lendo o símbolo $a$. Para esse efeito tem-se a transição de entrada:
Transição de Entrada. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFND.
A transição de entrada é a função de assinatura $\delta_\nil: Q\times \Sigma \to \mathcal{P}\at{Q}$ que, para cada $q\in Q, a\in\Sigma$, define o conjunto dos estados que podem ser alcançados a partir de $q$ lendo o símbolo $a$. Isto é: $$\delta_{\nil}\at{q,a} = \bigcup_{q’ \in \ecl\at{q}} \ecl\at{\delta\at{q’, a}}.$$
Por exemplo, seja $A$ o AFND definido pela tabela $$ \begin{array}{r|c|c|c||l} q & a & b & \nil & \ecl\at{q}\cr \hline 0 & & 01 & 1 & 01\cr 1 & 2 & 12 & & 1\cr f2 & 2& & 1 & 21 \end{array} $$ com o fecho vazio de cada estado já calculado e com o seguinte diagrama
| Transição de Entrada: Diagrama do AFND acima |
|---|
 |
A transição de entrada de alguns casos: $$ \begin{aligned} \delta_{\nil}\at{0, b} &= \set{0, 1, 2} \cr \delta_{\nil}\at{0, a} &= \set{2, 1} \end{aligned} $$ Neste caso, por exemplo, $2 \in \delta_{\nil}\at{0, a}$ porque $0 \trf{\nil} 1 \trf{a} 2$ é uma computação de $A$. Já $1 \in \delta_{\nil}\at{0, a}$ de duas maneiras diferentes: $1 \trf{a} 1$ e $1 \trf{a} 2 \trf{\nil} 1$.
Exercício: Calcule todas as transições de entrada deste exemplo.
Este “desvio” pelo fecho vazio e transição de entrada serve para formalizar as ferramentas que faltam para o objetivo desta secção: Mostrar que para cada AFND $A$ existe um AFD $A’$ “equivalente” no sentido em que $L(A) = L(A’)$.
Simulação de Não Determinismo. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFND.
O AFD equivalente a $A$ é o AFD $A’=\del{Q’, \Sigma, \delta’, q’_I, F’}$ em que:
- Estado Inicial $q’_I = \ecl\at{q_I}$.
- Transição $\delta’\at{q, a} = \bigcup_{p \in q} \delta_{\nil}\at{p, a}$.
- Estados de Controlo $Q’$ é definido recursivamente por
- base $q’_I \in Q’$.
- passo Se $q \in Q’$ então, para cada $a \in \Sigma, \delta’\at{q, a}\in Q’$.
- fecho Mais nenhum estado está em $Q’$.
- Estados Finais $F’ = \set{q \in Q’ \st q \cap F \not= \empty}$.
Neste caso $$L(A) = L(A’).$$
Por exemplo, para o AFND
| Um AFND para $\cl{a}\cl{b}\cl{c}$ |
|---|
 |
o cálculo de $\delta’$ e de $Q’$ é feito em conjunto:
$$ \begin{array}{r|c|c|c} \delta’ & a & b & c\cr \hline ifq’_I = \ecl\at{0} = \underline{02} & 02 & \alert{12} & \alert{1}\cr f\underline{12} & \alert{\empty} & 12 & 1 \cr f\underline{1} & \empty & \empty & 1 \cr \empty & \empty & \empty & \empty \end{array} $$
Os estados de $A’$ são conjuntos de estados de $A$. Para evitar uma notação muito pesada (por exemplo, $\set{0, 2}$) omitem-se as chavetas e as vírgulas (e escreve-se apenas $02$). O texto vermelho $\alert{xyz}$ representa estados “novos” na tabela e os estados finais de $A$ estão sublinhados. O respetivo diagrama é
| Um AFD equivalente ao AFND para $\cl{a}\cl{b}\cl{c}$ |
|---|
 |
O teorema/método da Simulação de Não Determinismo assegura que estes dois autómatos são equivalentes, isto é, reconhecem a mesma linguagem.
Conclusão
Uma vantagem dos AFD é que a computação é linear no comprimento da palavra pois executa exatamente $\len{p}$ passos para computar a resposta a $p \in L(A’)$ enquanto que para o AFND a computação da resposta $p \in L(A)$ é exponencial.
Este ganho no número de passos tem um custo: se o AFND $A$ tem $n$ estados então $A’$, o AFD equivalente, pode ter até $2^n$ estados.
Estão determinadas três equivalências:
- As ER e os AFND são equivalentes devido à Construção de Thompson e ao Algoritmo de Kleene.
- Os AFND e os AFD são equivalentes devido à Definição de AFND e à Simulação de Não Determinismo.
- Portanto, também as ER e os AFD são equivalentes.
Portanto
Os AFD proporcionam um bom modelo computacional para as ER.
Mas ainda há questões importantes a resolver. A próxima secção trata de formas de reduzir o tamanho dos AFD e de facilitar a construção automática de AFD e AFND antes de ser tratada a questão final, saber se “as linguagens regulares são adequadas para todas as linguagens de programação?”
Minimização e Composição de AFD
Principais operações com autómatos.
Introdução
Nas secções anteriores ficou provado que os AFD, AFND e as ER são equivalentes no sentido em que todos definem exatamente a classe das Linguagens Regulares.
Essa demonstração usa algoritmos para:
- Converter uma ER num AFND (Construção de Thompson).
- Converter um AFND numa ER (Algoritmo de Kleene).
- Simular um AFND por um AFD (Teorema da Simulação).
Comparando os AFD com os AFND:
| Autómato | Número de Estados | Comprimento das Computações |
|---|---|---|
| Determinista | Ineficiente | Eficiente |
| Não Determinista | Eficiente | Ineficiente |
Em termos de eficiência “absoluta” nenhum dos modelos (AFD e AFND) é superior. Mas enquanto não há nada a fazer em relação às computações não deterministas, em certos casos é possível reduzir o número de estados de um AFD.
Também interessa definir operações com autómatos que permitam acompanhar as operações das ER (união, concatenação, iteração) e também explorar outras possibilidades como a negação, a interseção e o processamento paralelo.
Minimização de AFD
Seja $L$ a linguagem das palavras binárias (sobre $\set{a, b}$) cujo quinto símbolo a contar do fim é $a$. Esta linguagem é definida pela ER $\clpar{a \cup b}a(a \cup b)(a \cup b)(a \cup b)(a \cup b)$ a que corresponde o diagrama e AFND seguinte:
| AFND para $\clpar{a \cup b}a(a \cup b)(a \cup b)(a \cup b)(a \cup b)$ |
|---|
 |
Exercício: A aplicação direta do teorema da simulação determinista a este AFND produz um autómato com $32$ estados de controlo.
A simulação de um AFND com $n$ estados de controlo pode produzir até $2^n$ estados no autómato determinista equivalente (exercício: porquê?).
Estados Indistintos
Dois AFD são equivalentes se aceitam a mesma linguagem. Por exemplo, para a linguagem $\cl{a}$:
| Autómato $A$ | Autómato $B$ |
|---|---|
 |  |
No Autómato $B$ os estados $I$ e $1$ são indistintos no seguinte sentido: Qualquer palavra processada a partir do estado $I$ é aceite SSE também for aceite se processada a partir do estado $1$.
Por exemplo, se $p=\nil$ e o autómato estiver no estado $I$ então $p$ é “aceite”. Também é “aceite” se o autómato estiver no estado $1$. Por outro lado $p=b$ é rejeitada quer o autómato esteja no estado $I$ quer no $1$.
Portanto, tanto $I$ como $1$ definem sempre os mesmos resultados em termos de aceitação/rejeição de palavras. Formalmente:
Estados Indistintos. Sejam $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFD e $i, j \in Q$ dois estados. Então $i$ é indistinto de $j$ se, para cada palavra $p \in \cl{\Sigma}$, $$\hat{\delta}\at{i, p} \in F \Leftrightarrow \hat{\delta}\at{j, p} \in F.$$ Em particular, se $i\in F$ e $j \in Q\setminus F$ não são indistintos.
Agrupando estados indistintos obtém-se um novo AFD com o número mínimo de estados para aquela linguagem regular, isto é, um Autómato Mínimo. Antes da respetiva definição formal é conveniente descrever um algoritmo para particionar os estados indistintos.
O objetivo é particionar o conjunto de estados em grupos de forma que dois estados estão no mesmo grupos se e só se são indistintos.
Partição dos Estados Indistintos. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFD:
- Iniciar a partição $P = \set{Q\setminus F, F}$.
- Enquanto existirem grupos $X, Y \in P$ com $i, j \in X$ e $a \in \Sigma$ tais que $\alert{\delta\at{i, a} \in Y, \delta\at{j, a} \not\in Y}$ ($X$ é inconsistente):
- Retirar $X$ da partição $P$: $P \to P \setminus \set{X}$.
- Acrescentar os estados de $X$ concordantes com $i$ em $a$: $P \to P \cup \set{k \in X\ :\ \delta\at{k, a} \in Y}$.
- Acrescentar os estados de $X$ discordantes de $i$ em $a$: $P \to P \cup \set{k \in X\ :\ \delta\at{k, a} \not\in Y}$.
Os passos deste ciclo refinam $X$ de forma a eliminar discordâncias de $i\in X$ sobre $a \in \Sigma$. O resultado é que a partição $P$ troca o grupo inconsistente $X$ por dois grupos mais pequenos mas “menos” inconsistentes, isto é, onde os estados estão “mais próximos” de serem indistintos.
A partição final é formada apenas por grupos consistentes, isto é, em que todos os estados são indistintos (no limite esses grupos têm apenas um estado). Os grupos dessa partição são os estados do AFD mínimo equivalente ao AFD inicial.
Autómato Mínimo. Sejam $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFD e $P$ a partição dos estados indistintos.
Para cada grupo $X \in P$ e cada $a \in \Sigma$ $$\delta’\at{X, a} = Y$$ em que $Y \in P$ é o grupo que contém $\delta\at{i, a}$ com $i \in X$.
O AFD Mínimo (ou reduzido) equivalente a $A$ é $A’ = \del{P, \Sigma, \delta’, q’_I, F’}$ em que:
- O estado inicial, $q’_I$, é o grupo de $P$ que contém o estado inicial $q_I$ de $A$.
- Os estados finais, $F’$, são os grupos de $P$ que estão contidos em $F$. Isto é
$$F’ = \set{X \in P \st X \subseteq F}.$$
A construção do autómato mínimo a partir da definição está sujeita a erros, pelo que são ilustrados de seguida dois métodos com vista a sistematizar e facilitar esse processo.
Dado o AFD $A$ pela seguinte tabela:
$$ \begin{array}{r|c|c} \delta & a & b\cr \hline i0 & 1 & 4 \cr f1 & 4 & 2 \cr 2 & 3 & 5 \cr f3 & 5 & 2 \cr 4 & 5 & 5 \cr 5 & 4 & 5 \end{array} $$
Construção do Autómato Mínimo por Tabelas de Transição
Iniciar grupos, detetar e assinalar inconsistências:
$$ \begin{array}{rll||r|ll||r|ll} \ & \delta & \ & \ & a & \ & \ & b \cr \hline 0 & \fbox{A} & \ & 1 & \alert{B} & \ & 4 & A & \ \cr f1 & B & \ & 4 & A & \ & 2 & A & \ \cr 2 & \fbox{A} & \ & 3 & \alert{B} & \ & 5 & A & \ \cr f3 & B & \ & 5 & A & \ & 2 & A & \ \cr 4 & \fbox{A} & \ & 5 & \alert{A} & \ & 5 & A & \ \cr 5 & \fbox{A} & \ & 4 & \alert{A} & \ & 5 & A & \ \end{array} $$
Separar inconsistências, detetar e assinalar novas inconsistências:
$$ \begin{array}{rll||r|ll||r|ll} \ & \delta & \ & \ & a & \ & \ & b\cr \hline 0 & A & A & 1 & B & B & 4 & A & \alert{C} \cr f1 & B & B & 4 & A & \alert{C} & 2 & A & A \cr 2 & A & A & 3 & B & B & 5 & A & \alert{C} \cr f3 & B & B & 5 & A & \alert{C} & 2 & A & A \cr \fbox{4} & \xcancel{A} & \alert{C} & 5 & A & \alert{C} & 5 & A & \alert{C} \cr \fbox{5} & \xcancel{A} & \alert{C} & 4 & A & \alert{C} & 5 & A & \alert{C} \end{array} $$
Não existem mais inconsistências: Agrupar e escrever a tabela do AFD mínimo:
$$ \begin{array}{r|c|c} \delta & a & b \cr \hline q’_I = A = \set{0, 2} & B & C \cr fB = \set{1, 3} & C & A \cr C = \set{4, 5} & C & C \end{array} $$
Construção do Autómato Mínimo por Diagramas
O diagrama do AFD dado é:
| AFD dado, com a partição inicial. |
|---|
 |
| $0, 2$ e $4,5$ discordam em $a$. |
 |
| Todos os grupos são consistentes. |
| Diagrama do ADF Mínimo |
 |
Foram descritos dois métodos para reduzir o número de estados de um AFD (minimizar). Ambos produzem o mesmo resultado: um autómato determinista com o menor número possível de estados e que seja equivalente a um AFD dado.
Embora isto não resolva completamente o potencial aumento exponencial do número de estados na passagem de AFND para AFD, produz um resultado ótimo, no sentido em que não existe melhor (isto é, por vezes o ótimo pode ainda ser “mau”).
Composição
A representação é importante. Intuitivamente, a numeração romana é equivalente à árabe no sentido que representam os mesmos números. Considere o Problema A: “Multiplicar
DXXXIXporXVII” e o Problema B: “Multiplicar89por17”. Embora os problemas A e B sejam o mesmo, é muito mais simples resolver B porque a representação árabe dos números “é compatível com” a multiplicação, ao contrário da representação romana.
As ER são construídas a partir da base ($\empty, \nil, a \in \Sigma$) usando operações bem definidas ($\cdot, \cup, \cl{}$). Desta forma é possível decompor uma ER nas suas componentes, o que proporciona uma importante forma de análise com vista a explorar as suas propriedades.
Por outro lado, em geral, os autómatos “surgem” completamente definidos e é difícil relacionar um autómato com outro. Dado que as ER, os AFD e os AFND são “equivalentes”, seria estranho que não fosse possível fazer também um estudo estruturado dos autómatos.
As operações com autómatos usam os Autómatos Bem Preparados pois estes têm uma forma adequada a serem “operados”.
Começando pela concatenação, a ideia intuitiva para $AB$ é “correr” primeiro $A$ e continuar em $B$:
Concatenação de AFND. Sejam $A = \del{Q^A, \Sigma, \delta^A, q^A_I, \set{q^A_F}}$ e $B = \del{Q^B, \Sigma, \delta^B, q^B_I, \set{q^B_F}}$ dois AFND bem preparados sobre um alfabeto comum, $\Sigma$, e com os estados de controlo disjuntos, $Q^A \cap Q^B = \empty$.
Então, a concatenação de $A$ com $B$ é o AFND $AB$, definido por $\del{Q^A \cup Q^B, \Sigma, \delta^{AB}, q^A_I, \set{q^B_F}}$ em que
$$\delta^{AB} = \delta^A \cup \delta^B \cup \set{\del{q^A_F, \nil, q^B_I}}.$$
A linguagem reconhecida por $AB$ é a concatenação da linguagem reconhecida por $A$ com a linguagem reconhecida por $B$: $$L\at{AB} = L\at{A}L\at{B}.$$
Exercício: $AB$ está bem preparado?
Por exemplo, se $A = \del{\set{0, 1}, \set{a, b}, 0, \set{\del{0, a, 1}}, \set{1}}$ e $B = \del{\set{2, 3}, \set{a, b}, \set{\del{2, b, 3}}, 2, \set{3}}$ (exercício: verifique que ambos são bem preparados e identifique as respetivas linguagens) então $$ AB = \del{\set{0, 1, 2, 3}, \set{a, b}, \set{\del{0, a, 1}, \del{2, b, 3}, \alert{\del{1, \nil, 2}}}, 1, \set{3}}. $$
Exercício: Traduza este exemplo para diagramas. Qual é a linguagem aceite por $AB$?
A união de autómatos é semelhante à concatenação. Intuitivamente, o primeiro “passo” é decidir se “corre” $A$ ou $B$. A computação da união termina a seguir a terminar a computação do autómato “escolhido” no início.
União de AFND. Sejam $A = \del{Q^A, \Sigma, \delta^A, q^A_I, \set{q^A_F}}$ e $B = \del{Q^B, \Sigma, \delta^B, q^B_I, \set{q^B_F}}$ dois AFND bem preparados sobre um alfabeto comum, $\Sigma$, e com os estados de controlo disjuntos, $Q^A \cap Q^B = \empty$.
Então, a união de $A$ com $B$ é o AFND $A\cup B$, definido por $\del{Q^A \cup Q^B \alert{\cup \set{q_I, q_F}}, \Sigma, \delta^{A\cup B}, q_I, \set{q_F}}$ em que
$$\delta^{A\cup B} = \delta^A \cup \delta^B \cup \set{\del{q_I, \nil, \set{q^A_I, q^B_I}}, \del{q^A_F, \nil, \set{q_F}}, \del{q^B_F, \nil, \set{q_F}}}.$$
A linguagem reconhecida por $A\cup B$ é a união da linguagem reconhecida por $A$ com a linguagem reconhecida por $B$: $$L\at{A\cup B} = L\at{A}\cup L\at{B}.$$
Continuando com os autómatos do exemplo acima: $$ A\cup B = \del{\set{0, 1, 2, 3, \alert{I, F}}, \set{a, b}, \set{\del{0, a, 1}, \del{2, b, 3}, \alert{\del{I, \nil, \set{1, 2}}, \del{1, \nil, F}, \del{3, \nil, F}}}, I, \set{F}}. $$
Exercício: Desenhe o diagrama do autómato $A\cup B$ acima.
Também a iteração segue o mesmo padrão:
Iteração de AFND. Sejam $A = \del{Q^A, \Sigma, \delta^A, q^A_I, \set{q^A_F}}$ um AFND bem preparado.
Então, a iteração de $A$ é o AFND $\cl{A}$, definido por $\del{Q^A \alert{\cup \set{q_I, q_F}}, \Sigma, \delta^{\cl{A}}, q_I, \set{q_F}}$ em que
$$\delta^{\cl{A}} = \delta^A \cup \set{\del{q_I, \nil, \set{q^A_I, q_F}}, \del{q^A_F, \nil, \set{q^A_I, q_F}}}.$$
A linguagem reconhecida por $\cl{A}$ é o fecho da linguagem reconhecida por $A$: $$L\at{\cl{A}} = \cl{L\at{A}}.$$
Exercício: Usando os exemplos acima, explicite as transições de $\cl{A}, A \cup \cl{B}, \cl{B}B \cup A\cl{B}$ e desenhe os respetivos diagramas.
A composição, união e iteração de AFND bem preparados são semelhantes em termos de requisitos e resultados. Para a negação e interseção é preciso sair desse padrão.
Intuitivamente, pensando em termos de autómatos deterministas, uma palavra é aceite se a computação termina num estado final e rejeitada se termina num estado não final. Portanto, basta trocar os estados finais com os não finais para se definir a linguagem complementar.
Quanto à interseção, uma vez definida a negação e a união, basta lembrar que para conjuntos, $A \cap B = \overline{\overline{A} \cup \overline{B}}$ e a mesma igualdade é válida para as linguagens regulares. Mas este processo é pouco prático.
Começando pela negação, é importante destacar que se aplica a autómatos deterministas ao contrário do que foi feito para a concatenação, união e iteração.
Negação de AFD. Sejam $A = \del{Q^A, \Sigma, \delta^A, q^A_I, F^A}$ um AFD.
Então, a negação de $A$ é o AFND $\overline{A}$, definido por $\del{Q^A, \Sigma, \delta^A, q^A_I, Q^A \setminus F^A}$.
A linguagem reconhecida por $\overline{A}$ é o complementar da linguagem reconhecida por $A$: $$L\at{\overline{A}} = \cl{\Sigma} \setminus L\at{A}.$$
| Um AFD e a sua negação |
|---|
| AFD para $\cl{a}$ |
 |
| AFD para $\cl{\Sigma} \setminus L\at{\cl{a}}$ |
 |
Paralelismo
É relativamente simples definir um autómato determinista que processa em paralelo outros dois (ou mais) autómatos também deterministas. Melhor, este método é suficientemente simples e geral para ter várias aplicações incluindo a união e interseção de AFD.
Em geral,
Autómato Paralelo. sejam $A = \del{Q^A, \Sigma, \delta^A, q^A_I, F^A}$ e $B = \del{Q^B, \Sigma, \delta^B, q^B_I, F^B}$ dois AFD sobre o mesmo alfabeto, $\Sigma$.
Seja $P^{A,B}_F = \del{Q^C, \Sigma, \delta^C, q^C_I, F}$ o AFD tal que:
- Estados de Controlo: $Q^C = Q^A \times Q^B$, isto é: um estado de controlo de $C$ é um par ordenado com um estado de $A$ e um estado de $B$.
- Transição: $\delta^C\at{ \del{i^A, i^B}, a} = \del{j^A, j^B}$ em que $j^A = \delta^A\at{i^A, a}, j^B = \delta^B\at{i^B, a}$, isto é: a transição de um estado é feira componente a componente.
- Estado Inicial: $q^C_I = \del{q^A_I, q^B_I}$, isto é: o estado inicial é o par de estados iniciais.
- Estados Finais: $F \subseteq Q^A \times Q^B$.
O conjunto dos estados finais fica como parâmetro porque proporciona uma grande flexibilidade aos autómatos paralelos. Por exemplo:
- União: Sejam $A, B$ dois AFD com estados finais $F^A, F^B$ respetivamente. Fazendo $F = \set{\del{i^A, i^B} \st i^A \in F^A \lor i^B \in F^B}$ tem-se $L\at{A} \cup L\at{B} = L\at{P^{A,B}_F}$. Note-se que uma palavra é aceite por $P^{A,B}_F$ se e só se é aceite por $A$ ou se é aceite por $B$.
- Interseção: Nas condições acima, seja $G = \set{\del{i^A, i^B} \st i^A \in F^A \land i^B \in F^B}$. Então $L\at{P^{A,B}_G} = L\at{A} \cap L\at{B}$. Note-se que uma palavra é aceite por $P^{A,B}_G$ se e só se é aceite por $A$ e por $B$.
Conclusão
Esta secção aprofundou o estudo dos AFD e AFND. Especificamente:
- Mostram-se dois métodos para minimizar um dado AFD, de modo a obter-se um AFD equivalente com o menor número possível de estados.
- Definiram-se as operações de concatenação, união e iteração de AFND, replicando as operações das ER.
- Definiu-se a negação e composição paralela de AFD. Com o processamento paralelo de AFD ficou trivial definir as operações de união e a interseção de AFD.
O Problema Principal de ALP — Dada uma linguagem $A$ e uma palavra $p$ no mesmo alfabeto, determinar se $p \in A$ — continua em aberto. As expressões regulares e os autómatos finitos (deterministas e não deterministas) verificam duas das três condições fundamentais:
- São computáveis (existe um algoritmo que recebe uma palavra e num número finito de passos “responde” se essa palavra está ou não na linguagem pretendida) e eficientes (um AFD processa uma palavra com $n$ símbolos em exatamente $n$ passos).
- Além disso é (relativamente) simples encontrar ER, AFND, AFD equivalentes.
Resta verificar se as linguagens regulares são adequadas para definir as linguagens de programação.
O Pumping Lemma
Os limites das linguagens regulares.
Introdução
Nas secções anteriores avançou-se na resolução do Problema Principal de ALP — Dada uma linguagem $A$ e uma palavra $p$ no mesmo alfabeto, determinar se $p \in A$ — com linguagens regulares.
As expressões regulares e os autómatos finitos (deterministas e não deterministas) são computáveis e eficientes mas ainda falta saber se são adequadas isto é, suficientemente expressivas para definir qualquer linguagem de programação.
As expressões algébricas, de uma forma ou outra, estão presentes em quase todas as linguagens de programação. Uma expressão algébrica é uma palavra como, por exemplo, 2 * (3 + 4) em que certas sub-palavras representam números (2, 3, 4), outras representam operações (+, *) e outras definem a estrutura da expressão ((, )).
A estrutura de uma expressão pode ser visualizada por uma árvore:
| Árvore de uma Expressão Algébrica |
|---|
 |
| Forma Alternativa |
 |
Naturalmente, pretende-se que no lugar de 2, 3 e 4 possam estar outras expressões algébricas e que as operações incluam, pelo menos, - e /. Conforme as expressões ficam mais complexas, maior a necessidade e a importância dos parêntesis.
A estrutura de um programa é semelhante à estrutura de uma expressão algébrica: Organiza-se como uma árvore com certos vértices “recursivos”. Em vez de números e operações, nas árvores dos programas os vértices têm instruções, expressões, diretivas, etc.
if x > 2:
a = double(x)
for i in range(a):
a = a + i
else:
a = 0
| Árvore de um Fragmento de Programa |
|---|
 |
Uma propriedade importante das expressões algébricas é que “os parêntesis têm de estar equilibrados”. Descartando os números e as operações, restam apenas os parêntesis e obtêm-se palavras como
(),()(),(())()(()()), que são “válidas” enquanto que as palavras)(,()), etc devem ser rejeitadas.
A “linguagem dos parêntesis equilibrados” é um excelente teste às linguagens regulares:
- Se for regular, as linguagens regulares são adequadas para definir as linguagens de programação. De facto, o
LISP(ver a página na wikipédia) é uma linguagem de programação que usa parêntesis e pouco mais. - Se não for regular, as linguagens regulares não permitem representar árvores de estruturas sintáticas como as expressões algébricas ou os programas
python. Nesse caso será necessário tentar outra abordagem para as linguagens de programação.
O problema que se coloca agora é o seguinte: Como saber se uma dada linguagem é, ou não, regular?
Consideremos alguns exemplos (sobre o alfabeto $\Sigma = \set{a, b}$):
- $A = \set{a^n \st n \geq 0} = L\at{\cl{a}}$ é regular.
- $\overline{A} = \cl{\Sigma}\setminus A$ também é regular porque é o complementar de uma linguagem regular (na secção anterior viu-se como fazer a negação de um AFD).
- $B = \set{b^n \st n \geq 0} = L\at{\cl{b}}$ também é regular, assim como são $AB, B\cl{A}(A \cup \overline{B})$, etc.
Neste casos o “exercício” é simples porque ou se encontra uma ER adequada ou são aplicados os resultados teóricos das secções anteriores para construir linguagens regulares.
Quanto a uma versão simples dos parêntesis equilibrados:
$$ E = \set{a^n b^n \st n \geq 0}. $$
As palavras de $E$ são $\nil, ab, aabb, aaabbb, \ldots, a^{91537}b^{91537}, \ldots$ Esta linguagem é regular?
De facto, como se prova que uma linguagem não é regular? O problema é o seguinte: Supondo que $A$ é uma linguagem regular. Como se prova que $A$ é regular? Basta encontrar uma ER (ou AFD ou AFND), $x$, adequada: $A = L(x)$.
Mas, se $A$ não for regular nenhuma ER é adequada. É preciso outro método para provar que $A$ não é regular.
Entra o Pumping Lemma.
O Pumping Lemma
Uma observação muito simples:
Um AFD com $n$ estados, quando processa uma palavra com mais do que $n$ símbolos, tem de “passar” mais do que uma vez em alguns estados, porque há mais símbolos do que estados.
Por exemplo, um AFD para $\cl{a}$, ilustrado abaixo, tem exatamente dois estados.
| AFD para $\cl{a}$ |
|---|
 |
Contando as entradas nos estados deste autómato:
| Palavra | Comprimento | Entradas em $I$ | Entradas em $E$ |
|---|---|---|---|
| $\nil$ | 0 | 0 | 0 |
| $a$ | 1 | 1 | 0 |
| … | … | … | … |
| $aaa$ | 3 | 3 | 0 |
| $aab$ | 3 | 2 | 1 |
| $aba$ | 3 | 1 | 2 |
| $abb$ | 3 | 1 | 2 |
| $baa$ | 3 | 0 | 3 |
| $bab$ | 3 | 0 | 3 |
| $bba$ | 3 | 0 | 3 |
| $bbb$ | 3 | 0 | 3 |
| … | … | … | … |
Todas as palavras de comprimento $3$ entram mais do que uma vez em algum estado do autómato. Claramente, o mesmo acontece para palavras de comprimento $4, 5, \ldots$
Em geral, seja $p$ uma palavra que entra duas (ou mais) vezes no estado $i$. Então pode escrever-se $p = uvw$ em que:
- $u$ é o prefixo de $p$ que entra pela primeira vez em $i$.
- $v$ é uma sub-palavra de $p$ que parte de $i$ e entra de novo em $i$.
- $w$ é o restante sufixo de $p$.
Como (o caminho de) $v$ começa e termina em $i$, a sub-palavra $v$ pode ser indefinidamente repetida, inclusivamente eliminada, que o estado final da computação não se altera. Isto é, o estado final para $p = p_1 = uvw$ é o mesmo que para $p_0 = uw, p_2 = uvvw, \ldots, p_{9375} = uv^{9375}w$.
Se $p$ for aceite, também são $p_0, p_1, p_2, \ldots$. E, se $p$ for rejeitada, também são $p_0, p_1, p_2, \ldots$
Formalmente:
Pumping Lemma. Seja $L$ uma linguagem regular e $k$ o número de estados de um AFD que a aceita.
Qualquer palavra $p \in L$ com $\len{p} > k$ pode ser escrita como $p = uvw$ em que:
- $\len{uv} < k$.
- $\len{v} > 0$.
- Para qualquer $n \geq 0$ também $uv^nw \in L$.
O Pumping Lemma é uma propriedade de todas as linguagens regulares. Dito de outra forma,
Se as conclusões do Pumping Lemma levarem a uma contradição é porque as hipóteses do Pumping Lemma não se verificam. Especificamente: a linguagem considerada não pode ser regular.
Revisitando a linguagem simplificada dos parêntesis equilibrados, $E = \set{a^mb^m \st m \geq 0}$.
- Supondo que $E$ é regular, também é aceite por um certo AFD.
- Seja $k$ o número de estados desse AFD.
- A palavra $p = a^kb^k \in E$.
- Pelo Pumping Lemma, como $\len{p} > k$ então $p = uvw$ em que:
- $\len{uv} < k$. Portanto, $uv$ só tem $a$.
- $\len{v} > 0$. Portanto $v$ tem pelo menos um $a$ e nenhum $b$.
- Para cada $n \geq 0$ também $p_n = uv^nw \in E$.
Em $p_n = uv^nw$, quando $v$ é repetido,o número de $a$ é alterado. Mas o número de $b$ continua a ser $k$. Portanto, quando $n \not = 1$, o número de $a$ deixa de ser igual ao número de $b$.
Isto é uma contradição. Por um lado, se $p_n = uv^nw\in E$ então tem o mesmo número de $a$ e de $b$ mas por outro, ao repetir $v$, $p_n$ fica com um número diferente de $a$ e de $b$.
Portanto a suposição inicial, de que a linguagem $E$ é regular, é falsa. A única conclusão possível é que $E$ não é uma linguagem regular.
O facto de $E$ não ser uma linguagem regular tem consequências profundas:
- Primeiro, encontrou-se uma linguagem que não é regular.
- Segundo, as linguagens regulares não são adequadas para definir linguagens de programação.
A incapacidade das linguagens regulares para definir a linguagem simplificada dos parêntesis equilibrados implica a incapacidade para definir as estruturas recursivas (como árvores) necessárias nas linguagens de programação.
Conclusão
O Pumping Lemma aplicado à linguagem $E= \set{a^mb^m \st m \geq 0}$ mostra que as linguagens regulares não são adequadas para definir linguagens de programação.
Portanto, é necessária outra abordagem para resolver o Problema Principal de ALP — Dada uma linguagem $A$ e uma palavra $p$ no mesmo alfabeto, determinar se $p \in A$ de forma computável, acessível e adequada.
Nem tudo está perdido. De facto, os conceitos introduzidos até aqui, as ER, os AFD e os AFND, vão continuar presentes no resto do curso e nas suas aplicações. O que muda é a importância que têm: Perdem o título de “candidato preferido” e passam a “contribuição necessária”.
O próximo capítulo define certas gramáticas formais que, como vai ser mostrado, generalizam as linguagens regulares e estão associadas aos autómatos de pilha, uma forma simples de autómato com memória ilimitada.
Autómatos Finitos — Exercícios
Os exercícios assinalados com “✓” serão resolvidos nas aulas práticas; Os assinalados com “†” têm elevada dificuldade. Todos os restantes devem ser resolvidos pelos alunos.
Autómatos Finitos Deterministas
Exercício 01
Para o AFD $A = \del{\set{q_0, q_1, q_2}, \set{a, b}, \delta, q_0, \set{q_2}}$ com a transição $\delta$ dada pela tabela
$$ \begin{array}{c|cc} \delta & a & b \cr \hline q_0 & q_0 & q_1 \cr q_1 & q_2 & q_1 \cr q_2 & q_2 & q_0 \end{array} $$
- Desenhe o diagrama de estados.
- Escreva as computações de $A$ para as palavras $abaa$ e $bbbabb$ referindo se são, ou não, aceites.
- Escreva uma expressão regular que represente a linguagem reconhecida por $A$.
Exercício 02
| AFD Exercício 02 |
|---|
 |
Seja $A$ o AFD dado pelo diagrama acima.
- Qual é o estado inicial, e quais são os estados finais?
- As palavras $0001$, $010101$ e $001110101101$ são aceites?
- Que palavras de $\del{01}^\ast$ estão em $L(A)$?
Exercício 03
Seja $A = \del{\set{0, 1, 2}, \set{x, y}, \set{\del{0,x,1}, \del{0,y,0}, \del{1,x,1}, \del{1,y,2}, \del{2,x,1}, \del{2,y,0}}, 0, \set{0}}$ um AFD.
- desenhe o diagrama de estados
- ✓ escreva uma expressão regular que represente a linguagem reconhecida por $A$
- ✓ repita a alínea anterior para o AFD $A’$ que apenas difere de $A$ no conjunto dos estados de aceitação, que no caso de $A’$ é $\set{0, 1}$
Exercício 04
Construa um autómato finito determinista que reconheça a linguagem das palavras…
- sobre $\set{a, b, c}$ em que todos os $a$’s precedem todos os $b$’s que, por sua vez, precedem todos os $c$’s (donde que todos os $a$’s precedem todos os $c$’s), podendo não haver nem $a$’s, nem $b$’s, nem $c$’s.
- sobre $\set{a, b}$ que não têm $aa$ como subpalavra.
- sobre $\set{a,b,c}$ em que cada $b$ é seguido imediatamente por $cc$.
- não vazias sobre $\set{a,b}$ em que o número de $a$’s é divisível por $3$.
Exercício 05
Construa um autómato finito determinista que reconheça a linguagem da ER $(ab)^\ast(ba)^\ast$.
Exercício 06
Calcule ER das linguagens reconhecidas pelos autómatos seguintes.
| a) | b) | |
 |  | |
| c) | d) | |
 |  | |
| e) | ||
 |
Exercício 07
Encontre um AFD que aceite a linguagem das palavras em $\del{0 \cup 1}^\ast$…
- com prefixo $01$.
- com subpalavra $00101$.
- expansões binárias dos naturais congruentes zero módulo $5$.
- com subpalavra $00$ e sufixo $01$.
- com subpalavra $00$ e não têm sufixo $01$.
- em que cada bloco de quatro letras consecutivas contém $01$.
Exercício 08
Encontre um AFD que aceite a linguagem das palavras…
- com prefixo $010$.
- com sufixo $101$.
- com subpalavra $010$ ou $101$.
- em que as últimas cinco letras têm três $0$s.
- $w$ tais que $\len{w}_1 + 2\len{w}_0$ é múltiplo de cinco.
- sobre o alfabeto $\set{1,2,3}$ onde a soma dos símbolos é múltiplo de cinco.
Computação Não Determinista
Exercício 09
Determine a linguagem (ER) dos AFND acima.
| a) | b) | c) |
 |  |  |
Exercício 10
Considere a linguagem de todos os números inteiros sem sinal, escritos em base $3$, em que o último algarismo ocorre anteriormente no número. Por exemplo, $1202$ e $00$ pertencem a esta linguagem, mas $1002$ e $1$ não. (Os números escritos em base $3$ só podem ter os algarismos $0, 1$ e $2$.)
- escreva uma expressão regular que a represente.
- defina um autómato finito que a reconheça.
- $\dagger$ apresente um autómato finito determinista que a reconheça (Sugestão: tente construí-lo diretamente, sem recorrer a qualquer algoritmo).
Exercício 11
 |
Considere o autómato definido no diagrama acima.
- Calcule o $\fecho\at{\set{0}}$ e o $\fecho\at{\set{1,2,3}}$.
- Calcule $\delta\at{\set{0},0}$ e $\delta\at{\set{2,3},1}$.
- Desenhe as árvores das computações de $011$ e $101$, indicando se são aceites ou rejeitadas.
Exercício 12
Seja $A = \del{\set{0,1,2}, \set{a,b,c}, \delta, 0, \set{1,2}}$ um autómato finito não determinista cuja função de transição é
$$ \begin{array}{c|cccc} \delta & a & b & c & \nil \cr \hline 0 & \set{0} & & \set{1} & \set{2} \cr 1 & & & \set{1} \cr 2 & & \set{1,2} \end{array} $$
Construa um autómato finito determinista equivalente a $A$, usando o algoritmo dado nas aulas, e apresente uma ER que represente a linguagem por ele reconhecida.
Exercício 13
✓ Repita o exercício anterior para o autómato finito não determinista $$B = \del{\set{0,1,2,3}, \set{m,n}, \delta, 0, \set{1}}$$ cuja função de transição é
$$ \begin{array}{c|ccc} \delta & m & n & \nil \cr \hline 0 & \set{1} & \set{2} & \set{1} \cr 1 & & \set{1,3} \cr 2 & & & \set{3} \cr 3 & \set{1,3} & \set{2} \end{array} $$
Exercício 14
✓ Considere a linguagem de todas as palavras sobre $\set{a,b}$ em que o antepenúltimo símbolo é $b$.
- defina um autómato finito (não determinista) que reconheça esta linguagem.
- aplicando o algoritmo dado nas aulas, construa um autómato finito determinista equivalente ao autómato finito da alínea anterior.
Exercício 15
$\dagger$ Repita o exercício anterior para a linguagem de todas as palavras sobre $\set{a,b}$ em que o terceiro e o antepenúltimo símbolos são $b$. São exemplos de palavras que pertencem a esta linguagem as palavras $aababaa$, $abbbbbbbb$, $abba$ e $bbb$.
Exercício 16
Sejam $A_1 = \del{Q_1, T, \delta_1, q_{01}, F_1}$ e $A_2 = \del{Q_2, T, \delta_2, q_{02}, F_2}$ dois autómatos finitos tais que $Q_1$ e $Q_2$ são disjuntos. Defina um autómato finito $B$ tal que $L\at{B} = L\at{A_1} \cup L\at{A_2}$.
Exercício 17
Defina um AFD equivalente ao AFND
$$N=\del{\set{p,q,r},\set{0,1},\delta,p,\set{q,r}}$$
em que
$$ \begin{array}{c|cc} \delta & 0 & 1 \cr \hline p & \set{p,q} & \set{p} \cr q & \emptyset & \set{r} \cr r & \emptyset & \emptyset \end{array} $$
Minimização e Composição de AFD
Exercício 18
✓ Aplicando o algoritmo dado nas aulas, construa o autómato finito determinista mínimo equivalente a $A = \del{\set{A,B,C,D,E,F}, \set{a,b}, \delta, A, \set{B,D}}$, com a função de transição
$$ \begin{array}{c|cc} \delta & a & b \cr \hline A & B & E \cr B & E & C \cr C & D & F \cr D & F & C \cr E & F & F \cr F & E & F \end{array} $$
e apresente uma expressão regular que represente $L\at{A}$.
Exercício 19
Considere o autómato finito não determinista $A = \del{\set{1,2,3,4,5}, \set{x,y}, \delta, 1, \set{5}}$, com a função de transição
$$ \begin{array}{c|cc} \delta & x & y \cr \hline 1 & \set{1} & \set{1,2} \cr 2 & \emptyset & \set{3} \cr 3 & \set{3} & \set{3,4} \cr 4 & \emptyset & \set{5} \cr 5 & \set{5} & \set{5} \end{array} $$
- construa o AFD equivalente a $A$.
- construa o AFD mínimo equivalente a $A$.
Exercício 20
✓ Considere a linguagem representada por $(aaa)^\ast$ reunida com $(aa)^\ast$.
- defina um autómato finito (não determinista) que reconheça aquela linguagem.
- construa um AFD equivalente ao autómato finito definido na alínea anterior.
- construa um AFD mínimo equivalente ao AFD obtido na alínea anterior.
Exercício 21
Repita o exercício anterior para a linguagem das palavras sobre $\set{a,b,c}$ que têm $ababc$ como subpalavra.
Exercício 22
✓ Construa um AFND que aceita a linguagem das palavras
- binárias com, pelo menos, três ocorrências de $010$;
- binárias com subpalavras $010$ e $101$;
- binárias (com subpalavra $010$ ou $101$) e (com sufixo $111$ ou $000$);
- binárias em que o $3n$-ésimo símbolo é $0$, para $n\geq 1$;
- binárias, de tamanho $3n$, e em que, para cada $1\leq k \leq n$, algum dos $3k-2$, $3k-1$ ou $3k$-ésimo símbolo é $0$;
- $0^n 1 0^m 1 0^q$ em que $q\equiv nm \bmod 3$;
Exercício 23
Encontre um AFND que aceite as palavras…
- com prefixo $010$ ou sufixo $110$.
- com pelo menos, duas ocorrências de $01$ e sufixo $11$.
- $0^n 1 0^m$ em que $n \equiv m\del{\bmod 3}$.
Exercício 24
- Sejam $A_1$ e $A_2$ dois AFND. Encontre um AFND $A$ tal que $L\at{A} = L\at{A_1}L\at{A_2}$.
- Seja $A$ um AFND. Encontre um AFND $B$ tal que $L\at{B} = L\at{A}^\ast$.
Exercício 25
Seja $A=\del{\set{p,q,r,s},\set{0,1},\delta,p,\set{q,s}}$ um AFND em que
$$\begin{array}{c|cc} \delta & 0 & 1 \cr \hline p & \set{q,s} & \set{q} \cr q & \set{r} & \set{q,r} \cr r & \set{s} & \set{p} \cr s & \emptyset & \set{p} \end{array}$$
Construa um AFND que aceite a linguagem complementar de $L\at{A}$.
Exercício 26
- Construa um AFD que aceite a linguagem binária das palavras em que o quinto símbolo a partir do fim é $0$.
- Converta (simule) cada um dos AFND seguintes num AFD:
-
$N = \del{ \set{p,q,r}, \set{0,1}, \delta,p, \set{q,r} }$ com transição $$ \begin{array}{c|cc} \delta & 0 & 1 \cr \hline p & p & pq \cr q & r &\emptyset \cr r & \emptyset & \emptyset \end{array}$$
-
Dados nos diagramas abaixo:
-
| 26.2 A | 26.2 B | 26.2 C |
|---|---|---|
 |  |  |
Exercício 27
Construa um AFD que aceite a linguagem das palavras que:
- Contêm as sub-palavras $010$ e $101$;
- Com sufixo $00$ ou $01$ ou $10$ (de duas maneiras);
- Ou (contêm as sub-palavras $001$ e $110$) ou (não contêm nem $001$ nem $110$);
- A quarta letra a partir do fim, e a quarta letra a partir do princípio são ambas $0$ (nota: $0110$ e $10101$ estão nesta linguagem);
O Pumping Lemma
Exercício 28
Mostre que as seguintes linguagens não são regulares:
- ✓ $L = \set{1^n+1^m=1^{n+m} \st n,m \geq 0}$.
- A linguagem das palavras capicua sobre $\set{a,b}$.
- $L = \set{aa^n b^n \st n \geq 0}$.
- $L = \set{0^n 1^{n+1} \st n \geq 0}$.
- $L = \set{a^n c b^n \st n \geq 0}$.
- $L = \set{a^nb^m \st m > n \geq 0}$.
Implementação
As indicações gerais para os exercícios de implementação são válidas aqui.
Uma Biblioteca para AFD
A biblioteca para AFD tem de verificar as condições indicadas a seguir.
- Os estados são números inteiros, os símbolos de entrada são
stringe as palavras são listas de símbolos. - Represente. Um AFD é representado por uma estrutura de dados
FSA(pode ser uma classe, umastruct, etc) com os seguintes atributos, que devem ser visíveis mas não modificáveis:initialStateo estado inicial.finalStateso conjunto dos estados finais.deltauma lista de triplos(q, s, p)que define a transição $\delta(q,s) = p$.
- Construção. Um AFD é construidos pela função/método
makeFSA(t,i,f)em que:té uma lista de triplos(q, s, p)como acima.ié o estado inicial.fé a lista dos estados finais.
- Sanidade. A função
wellFormed(fsa)oufsa.wellFormed()testa se os atributost,i,fdo argumento definem, de facto, um AFD. Quais são essas condições? - Implemente. A função
step(fsa, q, s)oufsa.step(q, s)devolve o estadopquandofsaestá no estadoqe lês.Se não existe transição para
(q, s)esta função devolve “não definido”.Em python “não definido” é
None, emjava/kotlinénull, em rust éOption::None, outras linguagens podem ou não definir “não definido” :D - Implemente. A função
proc(fsa, q, w)oufsa.proc(q, w)devolve o estado em quefsatermina se começar emqe ler a palavraw. Use o critério destepse a computação não continuar até ao fim. - Implemente. A função
accepts(fsa, q, w)oufsa.accepts(q, w), testa sewé aceite porfsa. Esta função deve devolver sempre um booleano. - Escrita. A função
repr(fsa)oufsa.repr()devolve umastringcom várias linhas:- A primeira linha tem o formato
i <Q>;em que<Q>é o estado inicial. - A segunda linha tem o formato
f <Q1> ... <Qn>;em que os<Qi>são os estados finais. - As restantes linhas têm o formato
<Q> <S> <P>;para representar a transição $\delta(q, s) = p$ dofsa. Deve existir uma linha destas para cada “aresta” do autómato. - N.B. todas as linhas terminam em “
;” e valores na mesma linha são separados por espaços.
- A primeira linha tem o formato
- † Leitura. A função
parseFSA(s)tem como argumento umastringno formato acima e devolve oFSAcorrespondente. A leitura do argumento deve descartar carateres “espaço” (\n\r\t) mas com cuidado. - † Escrita. Consulte a documentação da linguagem
dotusada para definir grafos. Implemente uma funçãoreprDOT(fsa)oufsa.reprDOT()para gerar um grafo numastringemdot. - † Sanidade. As funções
repreparseFSAdevem ser “inversas” uma da outra, no sentido em queparseFSA(s).repr() == separseFSA(fsa.repr()) == fsa. Embora estas igualdades não sejam exatamente igualdades, nem fáceis de implementar, teste-as com alguns casos simples.
Gramáticas e Autómatos de Pilha
 |
O Pumping Lemma aplicado à linguagem $E= \set{a^mb^m \st m \geq 0}$ mostra que as linguagens regulares não são adequadas para definir linguagens de programação.
Portanto, é necessária outra abordagem para resolver o Problema Principal de ALP — Dada uma linguagem $A$ e uma palavra $p$ no mesmo alfabeto, determinar se $p \in A$ de forma computável, acessível e adequada.
Neste capítulo definem-se certas gramáticas formais que generalizam as linguagens regulares e estão associadas aos autómatos de pilha, uma forma simples de autómato com memória ilimitada.
Gramáticas Independentes de Contexto
Uma especificação formal de linguagens mais capaz do que as expressões regulares.
Introdução
Nos capítulos anteriores desenvolveu-se, para as ER, AFD e AFND, um conjunto de técnicas computacionais eficientes, com vista a resolver o Problema Principal de ALP. Porém, com o Pumping Lemma, conclui-se que é necessária uma forma mais geral de definir linguagens.
As linguagens naturais têm uma certa estrutura que resulta de regras gramaticais. Por exemplo, “O gato bebe leite.” é válida em português mas “bebe. gato leite O” não. (N.B: neste exemplo os símbolos do alfabeto são as palavras da língua portuguesa — por exemplo, de um dicionário — e as palavras são sequências desses símbolos.)
Como descrever essas regras gramaticais? Por exemplo:
Frase : Sujeito Predicado
Sujeito : Artigo Substantivo
Predicado : Verbo Advérbio
Artigo : "o"
| "as"
Substantivo : "gato"
| "galinhas"
Verbo : "bebe"
| "voam"
Advérbio : "devagar"
| "baixinho"
Os termos Assim são variáveis e "entre aspas" são terminais.
Aplicando estas regras, obtém-se, por exemplo:
Frase : Sujeito Predicado
: Artigo Substantivo Predicado
: o Substantivo Predicado
: o gato Predicado
: o gato Verbo Advérbio
: o gato bebe Advérbio
: o gato bebe devagar
Também se obtêm frases com pouco sentido, como as gato voam devagar. Esses problemas, em princípio, podem ser tratados com regras mais sofisticadas. No entanto, também este exemplo sem sentido mantém a estrutura entre as diferentes partes da palavra: o Artigo está no início, etc. Isto é, usando aquelas regras nunca se obtém, por exemplo, devagar bebe o gato.
Gramáticas e Linguagens Independentes de Contexto
As Gramáticas Independentes do Contexto são uma forma simples de representar rigorosamente regras gramaticais como as ilustradas acima.
Gramática Independente do Contexto (GIC). Uma Gramática Independente do Contexto é um tuplo $G = \del{V, \Sigma, P, S}$ em que:
- Variáveis (ou Não Terminais): $V$ é um conjunto de símbolos, designados variáveis ou não terminais.
- Terminais: $\Sigma$ é um conjunto de símbolos, disjunto de $V$ (isto é, $V \cap \Sigma = \empty$), designados terminais.
- Produções (ou Regras): $P \subset V \times \clpar{V \cup \Sigma}$ é um conjunto finito. Os seus elementos são pares da forma $(A, p)$ com $A \in V$ e $p \in \clpar{V \cup \Sigma}$, designados produções ou regras e denotados $A \to p$.
- Símbolo Inicial: $S \in V$.
Numa GIC há dois tipos de símbolos: Os terminais, sem produções associadas e as variáveis, com produções associadas. Intuitivamente, as variáveis vão ser sucessivamente transformadas, até restarem apenas símbolos terminais.
É importante notar que o alfabeto das palavras é $\clpar{V \cup \Sigma}$ isto é, as palavras têm terminais e variáveis.
Esta mistura justifica a definição seguinte:
Prefixo (resp. Sufixo) Terminal. Seja $p \in \clpar{V \cup \Sigma}$ uma palavra formada por (zero ou mais) terminais e (zero ou mais) variáveis. Então, escrevendo $p = u q v$ em que $u, v \in \cl{\Sigma}$ e $q$ começa e termina por variáveis.
- O prefixo terminal de $p$ é $u$.
- O sufixo terminal de $p$ é $v$.
Isto é, $u$ é o maior prefixo só de terminais de $p$ e $v$ é o maior sufixo só de terminais.
Por exemplo, em $p = abSaB$ o prefixo terminal é $ab$ e o sufixo terminal é $\nil$.
A aplicação de regras de uma GIC transforma palavras. Formalmente:
Derivação. Sejam $G = \del{V, \Sigma, P, S}$ uma GIC, $u, v \in \clpar{V \cup \Sigma}$.
- Se $A \to p \in P$, então $uAv$ deriva diretamente $uwv$ e escreve-se $uAv \der upv$.
- Se existem $p_0, p_1, \ldots, p_n \in \clpar{V \cup \Sigma}$ tais que $$p = p_0 \der p_1 \der \cdots \der p_n = q$$ então $p$ deriva $q$ em $n$ passos e escreve-se $p \nder{n} q$.
- Se existe $n$ tal que $p \nder{n} q$ então $p$ deriva $q$ e escreve-se $p \ider q$.
As regras de uma gramática são aplicadas às variáveis de uma palavra e o resultado é uma nova palavra. A esse processo chama-se “derivação direta”. Se forem aplicadas $n$ derivações diretas obtém-se uma “derivação em $n$ passos”. Por fim, se o número exato de passos não for importante, tem-se uma “derivação”.
Por exemplo, dada a gramática $G = \del{ \set{S, A}, \set{a, b}, \set{ S \to bAb, S \to b, A \to AAa, A \to \nil}, S}$:
- $abSbAb \der abSbb$ pela regra $A \to \nil$.
- Também $abSbAb \der abbbAb$ pela regra $S \to b$.
- $abSbAb \der abbAbbAb$ pela regra $S \to bAb$.
Em certas circunstâncias é necessário especificar a GIC de onde estão a ser usadas as derivações. Nesse caso acrescenta-se o índice $_G$ e a notação das derivações fica $p \derg{G} q, p \nderg{n}{G} q, p \iderg{G} q$ para indicar que são usadas apenas produções de $G$.
Para escrever uma GIC é comum usarem-se as seguintes regras para simplificar a notação:
- Os terminais são representados por minúsculas e as variáveis por maiúsculas.
- Se nada for dito, $S$ é o símbolo inicial.
- As produções de cada variável ficam agrupadas e, entre si, separadas por “$\alt$”.
Por exemplo, a gramática acima fica completamente definida por $$ \begin{aligned} S &\to bAb \alt b \cr A &\to AAa \alt \nil \end{aligned} $$
As produções de uma gramática transformam palavras noutras palavras. Essa transformação tem a designação técnica de derivação e é a base para associar uma linguagem a uma GIC.
Linguagem Gerada. Seja $C = \del{V, \Sigma, P, S}$ uma GIC.
- O conjunto das palavras deriváveis a partir de $p \in \clpar{V \cup \Sigma}$ é $D\at{p} = \set{q \st p \cl{\der} q}$.
- A linguagem gerada por $G$ é $L\at{G} = \set{t \in \cl{\Sigma} \st S \ider t}$.
- Neste caso diz-se que $L\at{G}$ é uma Linguagem Independente do Contexto.
- Duas gramáticas são equivalentes se geram a mesma linguagem.
Observação. As palavras da linguagem gerada são só de terminais. Isto é: $L(G) \subseteq \cl{\Sigma}$.
Tal como foi feito para as ER, os AFD e AFND, a equivalência entre GIC assenta na linguagem associada.
Por exemplo, qual é a linguagem gerada por $G = S \to aSb \alt \nil$?
- Da produção $S \to \nil$ resulta a derivação $S \ider \nil$. Portanto $\nil \in L\at{G}$.
- Da derivação $S \nder{S \to aSb} aSb \nder{S \to \nil} ab$ resulta que $ab \in L\at{G}$.
- Igualmente, de $S \nder{S \to aSb} aSb \nder{S \to aSb} aaSbb \nder{S \to \nil} aabb$ conclui-se que $aabb \in L\at{G}$.
- Sucessivamente, $aaabbb, a^4b^4, \ldots, a^mb^m, \ldots \in L\at{G}$.
Portanto, $G = S \to aSb \alt \nil$ gera a linguagem simplificada dos parêntesis equilibrados, $E = \set{a^mb^m \st m \geq 0}$.
A linguagem $E$, usada para mostrar que as linguagens recursivas não são adequadas para definir linguagens de programação é a linguagem gerada por uma GIC com apenas duas produções.
Este exemplo é um sinal positivo para resolução do Problema Principal de ALP, pelo menos em termos da adequação. Falta ainda aprofundar casos mais complexos de adequação e tratar dos aspetos da computação e da eficiência.
Recursividade
Donde vem a capacidade das GIC para gerar tão facilmente $E$, quando as ER falharam?
Olhando de novo para a GIC em questão, $G = S \to aSb \alt \nil$, destaca-se a regra $S \to aSb$. O “$S$” em “$aSb$” permite “repetir indefinidamente” o $S$, como um ciclo.
Esta possibilidade de “repetições indefinidamente” está além da capacidade expressiva das ER. Porém, é uma espada de dois gumes, que levanta problemas novos. Por exemplo, que palavras são geradas pela GIC $S \to Sa$?
Formalmente, a produção $S \to aSb$ é “diretamente recursiva” e a recursão pode surgir de várias formas:
Produção Recursiva. Não Terminal Recursivo, Derivação Recursiva. Sejam $G = \del{V, \Sigma, P, S}$ uma GIC, $A \in V$ e $p, u, v \in \clpar{V \cup \Sigma}$.
- Uma produção da forma $A \to uAv$ é diretamente recursiva.
- Uma variável $A$ é recursiva se $A \to p \ider uAv$ (isto é, $A \ider uAv$ em um ou mais passos).
- Uma derivação da forma $A \ider p \ider uAv$ onde $A$ não ocorre em $p$ é indiretamente recursiva.
Por exemplo,
- $S \to aSb$ é uma produção diretamente recursiva.
- No exemplo anterior, $S$ é uma variável recursiva.
- Na gramática $S \to aAb, A \to cSc \alt \nil$, a derivação $S \der aAb \der acScb$ é indiretamente recursiva.
Mais tarde serão tratadas várias situações relacionadas com a recursividade mas por enquanto importa aprofundar mais aspetos das derivações.
Em primeiro lugar importa assegurar que, numa derivação $p \nder{n} q$, as sub-derivações de uma variável em $p$ não são afetadas pelas sub-derivações de outras variáveis também em $p$.
Por exemplo, supondo que numa certa CIG $aXbYc \nder{7} acccbaaac$, é intuitivamente evidente que os $ccc$ resultam de $X$ e apenas de $X$ e que os $aaa$ resultam apenas do $Y$ e que, no total, fizeram-se $7$ derivações.
Mas a evidência intuitiva precisa de um apoio rigoroso:
Independência das Sub-Derivações. Seja $G = \clpar{V, \Sigma, P, S}$ uma GIC e $p \nder{n} q$ uma derivação em $G$ onde
$$p = p_1 A_1 p_2 A_2 \cdots p_k A_k p_{k+1}$$
com os $p_i \in \cl{\Sigma}$ (portanto, palavras só de terminais) e os $A_i \in V$.
Então existem palavras $q_i \in \clpar{V \cup \Sigma}$ tais que:
- Para cada $i$, $A_i \nder{n_i} q_i$.
- $q = p_1 q_1 p_2 q_2 \ldots p_k q_k p_{k+1}$.
- $\sum_{i = 1}^k n_i = n$.
A independência está na afirmação de que o resultado $q = p_1 q_1 p_2 q_2 \ldots p_k q_k p_{k+1}$ é obtido isoladamente em cada variável, $A_i \nder{n_i} q_i$.
Por exemplo, dada a gramática $S \to cAcBc, A \to aA \alt \nil, B \to Bb \alt \nil$, a derivação em $5$ passos $$\underbrace{cAcBc}_p \der c\underline{aA}cBc \der c\underline{a}cBc \der cac\underline{Bb}c \der cac\underline{Bbb}c \der \underbrace{cac\underline{bb}c}_q$$ tem sub-derivações:
- $A \der aA \der a$ com dois passos; $A = A_1 \nder{2} a = q_1$.
- $B \der Bb \der Bbb \der bb$ com três passos; $B = A_2 \nder{3} bb = q_2$
- $q = c q_1 c q_2 c$.
Derivação Esquerda/Direita
Considerando a GIC $S \to SS \alt aSb \alt \nil$, a partir do símbolo inicial, $S$, há três opções para “escolher a produção”. Se a escolha for $S \to SS$, fica-se com a derivação $S \der SS$, se for $S \to aSb$ a derivação é $S \der aSb$ e também $S \der \nil$ é uma derivação possível.
Em $SS$ há duas opções para “escolher a variável”. A primeira $S$ ou a segunda? Se for a primeira, obtém-se $aSbS$, $SSS$ e $S$ mas se for a segunda os resultados possíveis são $SSS$, $SaSb$ e $S$.
As regras das derivações permitem duas escolhas:
- Que variável substituir?
- Com que produção dessa variável?
Se por um lado estas escolhas permitem “capacidade expressiva” (o que é bom: as ER não são suficientemente expressivas) por outro lado as escolhas têm um custo elevado (exponencial) na eficiência computacional de futuros algoritmos sobre CIG e LIC.
Uma boa solução para este dilema restringe as escolhas sem sacrificar a “capacidade expressiva”.
Derivação Esquerda. Derivação Direita.
Numa derivação esquerda é escolhida a variável mais à esquerda em todos os passos. Nas derivações esquerdas o símbolo $\derop$ é substituído por $\deropL$.
Numa derivação direita é escolhida a variável mais à direita em todos os passos. Nas derivações direitas o símbolo $\derop$ é substituído por $\deropR$.
Seja $G = \del{V, \Sigma, P, S}$ uma GIC. Para cada $p \in \cl{\Sigma}$, $$p \in L\at{G} \iff S \ider p \iff S \iderL p \iff S \iderR p.$$
Isto é, numa derivação esquerda escolhe-se sempre a primeira variável e numa derivação direita escolhe-se sempre a última. A “capacidade expressiva” não fica prejudicada porque qualquer palavra só de terminais que seja gerada pela GIC também é gerada por uma derivação esquerda e também é gerada por uma derivação direita.
Por exemplo, continuando com a gramática $S \to SS \alt aSb \alt \nil$, como derivar $abaabb$?
- Sem restrições, uma solução é $S \der SS \der aSbS \der aSbaSb \der abaSb \der abaaSbb \der abaabb$. Nuns passos foi escolhida a primeira variável, noutros a última.
- Derivação esquerda: $S \derL SS \derL aSbS \derL abS \derL abaSb \derL abaaSbb \derL abaabb$.
- Derivação direita: $S \derR SS \derR SaSb \derR SaaSbb \derR Saabb \derR aSbaabb \derR abaabb$.
Árvore de Derivação
As derivações podem ser representadas graficamente por diagramas em árvore.
Árvore de Derivação. Seja $G = \del{V, \Sigma, P, S}$ uma GIC e $S\ider p$ uma derivação de $G$.
A árvore da derivação $S \ider p$ é formada por:
- Raiz: O símbolo inicial $S$.
- Filhos: Se a produção $A \to x_1 x_2 \cdots x_n$, com $x_i \in V \cup \Sigma$ for a produção usada para substituir a variável $A$ então o vértice $A$ tem filhos $x_1, x_2, \ldots x_n$ por essa ordem.
- Folhas Vazias: Se $A \to \nil$ for a produção usada para substituir a variável $A$ então o vértice $A$ tem $\nil$ como único filho.
Uma palavra $p$ tem árvore de derivação $T$ se $p$ for a concatenação das folhas de $T$ lidas da esquerda para a direita.
Por exemplo, a derivação $S \nder{S \to aSb} aSb \nder{S \to aSb} aaSbb \nder {S \to \nil} aabb$ tem a seguinte árvore:
| Exemplo de Árvore de Derivação |
|---|
 |
Lendo as folhas da esquerda para a direita obtém-se $aabb$, a palavra derivada.
Ambiguidade
Um problema (ver Dangling Else na wikipedia) que ocorre frequentemente em várias linguagens de programação, e que é responsável por erros difíceis de detetar e com consequências graves, pode ser ilustrado no seguinte exemplo:
if (a) if (b) s1; else s2;
Este fragmento tanto pode ser tratado como
if (a) {
if (b) s1;
else s2;
}
ou como
if (a) {
if (b) s1;
}
else s2;
No primeiro caso, se a for falso não corre nem s1 nem s2. No segundo caso, se a for falso corre s2.
O que acontece se a for “inimigo detetado”, s2 “lançar mísseis” e b testa “cenário simulado”?
Este problema resulta diretamente da gramática porque a palavra if (a) if (b) s1; else s2; tem duas derivações diferentes, uma que associa o else ao primeiro if e outra que o associa ao segundo.
Formalmente,
Gramática Ambígua. Linguagem Inerentemente Ambígua.
- Uma gramática $G$ é ambígua se alguma palavra de $L\at{G}$ tem:
- duas árvores de derivação distintas ou
- duas derivações esquerdas distintas ou
- duas derivações direitas distintas.
- Uma linguagem é inerentemente ambígua se não for gerada por uma gramática não ambígua.
Nesta definição é importante lembrar e distinguir o seguinte:
- Uma linguagem pode ser gerada por várias gramáticas equivalentes. Algumas dessas gramáticas podem ser ambíguas e outras não. Por isso, “ambígua” é uma propriedade que diz respeito às gramáticas.
- Também pode acontecer que todas as gramáticas que geram uma certa linguagem sejam ambíguas. Esta situação é uma caraterística da linguagem, não das gramáticas que a geram. Por isso “inerentemente ambígua” é uma propriedade que diz respeito às linguagens.
Um exemplo de uma linguagem inerentemente ambígua é:
$$\set{a^i b^j c^k \st i, j, k \geq 0}$$
A gramática $S \to SS \alt \nil$ é ambígua porque $S \derR \nil$ e $S \derR SS \derR S \derR \nil$ são duas derivações direitas de $\nil$. Esta gramática é equivalente a $S\to \nil$ que não é ambígua (exercício: porquê?).
Como é que as LIC se relacionam com as LR? O que foi feito nos capítulos anteriores está “perdido” ou as GIC estendem as ER?
Gramáticas Regulares e Simulação de AFND
Como definir linguagens regulares com GIC?
Gramática Regular. Uma gramática $G = \del{V, \Sigma, P, S}$ é regular se todas as suas produções têm uma das formas seguintes: $$ \begin{aligned} A &\to a \cr A &\to aB \cr A &\to \nil \end{aligned} $$ com $A, B \in V$ e $a \in \Sigma$.
O interesse desta definição é que
Se $G$ é uma GIC regular então $L\at{G}$ é uma linguagem regular.
A demonstração desta afirmação está fora do âmbito de ALP. A consequência das gramáticas regulares é que as GIC podem gerar algumas linguagens regulares*. Será que podem gerar todas?
Simulação de AFND por GIC. Seja $A = \del{Q, \Sigma, \delta, q_I, F}$ um AFND. A GIC equivalente a $A$ é $G = \del{V, \Sigma, P, S}$ em que:
- variáveis - estados. $V = \set{X_q \st q \in Q}$.
- símbolo inicial - estado inicial. $S = X_{q_I}$.
- produções - estados finais. Se $q \in F$ então $X_q \to \nil \in P$.
- produções - transições $q \tof{a} p$. Para cada $a \in \Sigma$, se $p \in \delta\at{q, a}$ então $X_q \to aX_p \in P$.
- produções - transições $q \tof{\nil} p$. Se $p \in \delta\at{q, \nil}$ então $X_q \to X_p \in P$.
Neste caso $L\at{A} = L\at{G}$.
Dado um AFND qualquer, aplicando este método, obtém-se uma GIC equivalente no sentido em que a linguagem aceite pelo AFND é gerada pela GIC. Portanto as LIC incluem todas as LR.
Por exemplo, dado o AFND antes usado para ilustrar o Algoritmo de Kleene:
| AFND equivalente a $\del{\nil \cup a} \clpar{b \cup b\clpar{a \cup b}a}$ |
|---|
 |
vai construir-se a GIC em que:
- As variáveis são $X_0, X_1, X_2, X_3$.
- O símbolo inicial é $S = X_0$.
- As transições e os estados finais definem as seguintes produções: $$ \begin{aligned} X_0 &\to aX_1 \alt b X_2 \alt X_1 \cr X_1 &\to bX_1 \alt bX_3 \alt \nil \cr X_2 &\to X_3 \cr X_3 &\to aX_1 \alt a X_3 \alt b X_2 \end{aligned} $$
A palavra abaabb é aceite pelo AFND, pela computação
$$ 0 \trf{a} 1 \trf{b} 3 \trf{a} 3 \trf{a} 1 \trf{b} 1 \trf{b} 1 \in F. $$
Será gerada pela GIC? $$ X_0 \der aX_1 \der abX_3 \der abaX_3 \der abaaX_1 \der abaabX_1 \der abaabbX_1 \der abaabb. $$
Este exemplo também ilustra como a produção $X_q \to a X_p$ da GIC representa a transição $q \trf{a} p$ do AFND.
Conclusão
As GIC foram introduzidas depois de se ter constatado, no capítulo anterior, que as linguagens regulares são insuficientes para definir as linguagens de programação.
- Logo um dos primeiros exemplos de GIC permitiu definir a linguagem simplificada dos parêntesis equilibrados, o que é um indicador positivo para as GIC.
- Outro exemplo, as expressões algébricas, permitiu ilustrar como tratar o problema da ambiguidade.
- A questão da relação entre as LR e as LIC ficou resolvida com a simulação de AFND por uma GIC regular.
Embora as GIC pareçam um candidato razoável para descrever as linguagens de programação, falta tratar as questões da computação: Como responder algoritmicamente, de forma eficiente, à questão $p \in L\at{G}$?
Autómatos de Pilha
Um modelo computacional simples com memória ilimitada.
Introdução
Embora as GIC pareçam um candidato razoável para descrever as linguagens de programação, falta tratar as questões da computação: Como responder algoritmicamente, de forma eficiente, à questão $p \in L\at{G}$?
Intuitivamente, nos AFD e AFND a “memória” está representada pelos estados e portanto é limitada à priori, independentemente da palavra que vai ser processada. Por isso é que a linguagem $E = \set{a^m b^m \st m \geq 0}$ “escapa” ao reconhecimento pelos AFD e AFND — “é preciso memorizar quantos $a$ foram lidos” e esse número é arbitrariamente grande.
As “pilhas” são uma forma simples de “memória ilimitada”. Numa pilha podem ser colocados e retirados símbolos no “topo”. A transição depende não só do estado e do símbolo da palavra mas também do símbolo que está no topo da pilha.
Autómatos de Pilha e Gramáticas Independentes de Contexto
Tal como foi feito para os AFD e AFND, depois da definição de autómato segue-se a configuração e computação e palavra aceite e linguagem reconhecida.
Autómato de Pilha (AP). Um Autómato de Pilha (AP) é um tuplo $A = \del{Q, \Sigma, \Gamma, \delta, q_I, F}$ em que:
- Estados de Controlo, Alfabeto de Entrada, Estado Inicial, Estados Finais $Q, \Sigma, q_I, F$ são como nos AFD.
- Alfabeto da Pilha $\Gamma$ é um conjunto finito de símbolos.
- Transição $\delta$ é uma função com assinatura
$$\delta : Q \times \del{\Sigma \cup \set{\nil}} \times \del{\Gamma \cup \set{\nil}} \to \mathcal{P}\at{Q \times \del{\Gamma \cup \set{\nil}}}$$
Importa notar o seguinte:
A transição depende do estado de controlo, do símbolo de entrada e do símbolo no “topo” da pilha e define o novo estado de controlo e o novo símbolo no “topo” da pilha.
As computações dos AP são não deterministas, como resulta da assinatura da transição, na parte “$\mathcal{P}\at{\cdots}$”. Formalmente:
Configuração. Computação. (AP). Seja $A = \del{Q, \Sigma, \Gamma, \delta, q_I, F}$ um AP.
Uma Configuração é um triplo $\del{i, p, \alpha} \in Q \times \cl{\Sigma} \times \cl{\Gamma}$.
A Configuração Inicial para $p \in \cl{\Sigma}$ é $\del{q_I, p, \nil}$.
Uma Computação é uma sequência de passos dos seguintes tipos:
- AFND $\del{i, ap, \nil} \tr \del{j, p, \nil}$ se $\del{j, \nil} \in \delta\at{i, a, \nil}$ e $p \in \cl{\Sigma}$.
- Remove $\del{i, ap, A\alpha} \tr \del{j, p, \alpha}$ se $\del{j, \nil} \in \delta\at{i, a, A}$ e $p \in \cl{\Sigma}$.
- Acrescenta $\del{i, ap, \alpha} \tr \del{j, p, A\alpha}$ se $\del{j, A} \in \delta\at{i, a, \nil}$ e $p \in \cl{\Sigma}$.
- Troca $\del{i, ap, A\alpha} \tr \del{j, p, B\alpha}$ se $\del{j, B} \in \delta\at{i, a, A}$ e $p \in \cl{\Sigma}$.
Informalmente, os tipos de passos de uma computação são
| Tipo | Anterior | Seguinte | Condição | Observação |
|---|---|---|---|---|
| AFND | $\del{i, ap, \nil}$ | $\del{j, p, \nil}$ | $\del{j, \nil} \in \delta\at{i, a, \nil}$ | A pilha não é “usada”. |
| Remove | $\del{i, ap, A\alpha}$ | $\del{j, p, \alpha}$ | $\del{j, \nil} \in \delta\at{i, a, A}$ | $A$ no topo é substituído por $\nil$. |
| Acrescenta | $\del{i, ap, \alpha}$ | $\del{j, p, A\alpha}$ | $\del{j, A} \in \delta\at{i, a, \nil}$ | $\nil$ no topo é substituído por $A$. |
| Troca | $\del{i, ap, A\alpha}$ | $\del{j, p, B\alpha}$ | $\del{j, B} \in \delta\at{i, a, A}$ | $A$ no topo é substituído por $B$. |
O critério de aceitação de uma palavra depende da configuração final.
Palavra Aceite. Linguagem Reconhecida. (AP) Seja $A = \del{Q, \Sigma, \Gamma, \delta, q_I, F}$ um AP. A palavra $p \in \cl{\Sigma}$ é aceite por $A$ se existe uma computação $$ \del{q_I, p, \nil} \trf{\ast} \del{q, \nil, \nil},\quad q \in F.$$
A linguagem reconhecida (ou aceite) por $A$ é o conjunto das palavras aceites por $A$.
A condição $\del{q, \nil, \nil},\quad q \in F$ especifica que:
- A computação chegou a um estado final,
- Todos os símbolos de $p$ foram processados e
- A pilha está vazia.
Além disso, a condição de aceitação depende de existir uma computação naquelas condições. Outras computações podem não ser assim. Portanto, para uma palavra ser rejeitada é necessário que nenhuma computação verifique todas.
Diagramas de AP
Os diagramas dos AP seguem as mesmas regras dos AFD e AFND, sendo apenas necessário indicar as operações na pilha.
Por exemplo, o AP por
- Estados de Controlo $Q = \set{0, 1}$.
- Alfabeto de Entrada $\Sigma = \set{a, b}$.
- Alfabeto da Pilha $\Gamma = \set{X}$.
- Estado Inicial $q_I = 0$.
- Estados Finais $F = \set{1}$.
- Transição
$$ \begin{array}{c||c|c||c|c||c|c||} q & a, \nil & a, X & b, \nil & b, X & \nil, \nil & \nil, X\cr \hline 0 & 0,X & & && 1, \nil \cr f1 & & & & 1, \nil \end{array} $$
tem o seguinte diagrama
| Diagrama de AP para $\set{a^m b^m \st m \geq 0}$ |
|---|
 |
Note-se que na tabela da transição as colunas descrevem não só todas as possibilidades $\Sigma \times \Gamma$ como também os casos com $\nil$.
Descrevendo os passos das computações por $$i, ap, A\alpha \trf{a, A/B} j, p, B\alpha$$ algumas computações deste AP são:
- De $\nil$: $0,\nil,\nil \trf{\nil, \nil/\nil} 1,\nil,\nil$. Como $1$ é final e a entrada e a pilha estão vazias, $\nil$ é aceite.
- De $a$:
- $0,a,\nil \trf{a,\nil/X} \boxed{0, \nil, X} \trf{\nil, \nil/\nil} 1, \nil, X$. Esta computação poderia ter parado em $ \boxed{0, \nil, X}$, que não aceita $a$ tal como a última configuração.
- Em alternativa, $0, a, \nil \trf{\nil, \nil/\nil} 1, a, \nil$ que não aceita $a$.
- Como não há mais computações de $a$ esta palavra é rejeitada.
- De $b$: $0, b, \nil \trf{\nil, \nil/\nil} 1, b, \nil$ é a única possibilidade e rejeita $b$.
- De $ab$: $0, ab, \nil \trf{a, \nil/ X} 0, b, X \trf{\nil, \nil/\nil} 1, b, X \trf{b, X/\nil} 1, \nil, \nil$ aceita.
- De $ba$: é semelhante à computação de $b$.
A computação de $ab$ ilustra bem o uso da pilha como dispositivo de memória. Por cada $a$ lido da entrada é acrescentado uma “conta” $X$ à pilha. Quando se passa do estado $0$ para $1$ cada $b$ desconta a “conta” do topo. Se o número de $b$ for igual ao número de $a$ então no fim de processar todos os $b$ a pilha fica vazia.
Aquele AP tem mais “estrutura” do que apenas a contagem de $a$ e $b$. Por exemplo, $ba$ tem um $a$ e um $b$ mas é rejeitada devido à forma como o AP proíbe ler $a$ depois de começar a ler $b$.
Árvore das Computações
As computações dos AP, em geral, não são deterministas. Isto significa que, dada uma palavra para processar, o AP “gera uma árvore”, em vez de uma única sequência.
Árvore das Computações. Seja $A = \del{Q, \Sigma, \Gamma, \delta, q_I, F}$ um AP e $p \in \cl{\Sigma}$. A árvore das computações de $p$ por $A$ é formada por:
- Raíz: A configuração $\del{q_I, p, \nil}$.
- Filhos: Se $v$ for um vértice da árvore, para cada configuração $u$ tal que $v \tr u$ por $A$ então $u$ é um filho de $v$.
Por exemplo, no AP acima, a palavra $aabb$ tem a seguinte árvore de computação:
| Árvore das Computações de $aabb$ | Autómato de Pilha |
|---|---|
 |  |
Variantes de AP
O tipo de transições permitidas pela definição de AP é um caso intermédio entre:
- Autómato Atómico é um AP que só tem transições do tipo
- $(j, \nil) \in \delta\at{i, a, \nil}$: AFND.
- $(j, \nil) \in \delta\at{i, \nil, A}$: Remove, mas não lê da entrada.
- $(j, A) \in \delta\at{i, \nil, \nil}$: Acrescenta, mas não lê da entrada.
- Autómato Estendido é um AP que também permite transições do tipo $(j, \beta\alpha) \in \delta\at{i, a, A\alpha}$ em que o topo da pilha é substituído por mais do que um símbolo ($A/\beta$).
Estas variantes são equivalentes, no sentido em que um AP de uma variante pode ser transformado num AP doutra.
GIC e AP
Os AP definem o aspeto computacional das CIG mas essa ligação ainda não foi definida:
Simulação de GIC por AP. Seja $G = \del{V, \Sigma, P, S}$ uma GIC.
O AP $$A = \del{\set{q}, \Sigma, \Sigma \cup V, \delta, q, \set{q}}$$ em que a transição é definida por
- Para cada variável $A \in V$,
$$\delta\at{q, \nil, A} = \set{ \del{q, p} \st A \to p \in P}$$
- Para cada terminal $a \in \Sigma$,
$$\delta\at{q, a, a} = \set{ \del{q, \nil}}$$
é equivalente a $G$ no sentido em que $$L\at{G} = L\at{A}$$ se a pilha for iniciada com $S$.
Esta definição/transformação/teorema define como obter um AP equivalente a uma GIC dada. Embora o processo inverso fique fora do âmbito de ALP, para os efeitos pretendidos isto é suficiente.
Embora a condição sobre a inicialização da pilha contradiga a definição de AP, pode ser facilmente contornada. Basta definir um novo estado inicial $q_I$ e acrescentar a transição $\delta\at{q_I, \nil, \nil} = \set{ \del{q, \nil, S}}$.
Por exemplo, dada a GIC $S \to aSb \alt \nil$ o AP equivalente é
| AP da GIC $S \to aSb \alt \nil$ |
|---|
 |
As arestas associadas aos terminais e a cada variável são normalmente agrupadas de forma a facilitar a leitura do diagrama.
Este AP é equivalente ao anterior e à GIC da linguagem simplificada dos parêntesis equilibrados. Neste caso as produções da GIC podem ser “lidas” diretamente das arestas do AP.
Algumas computações deste AP:
- De $\nil$: $q_I, \nil, \nil \trf{\nil, \nil/S} q, \nil, S \trf{\nil, S/\nil} q, \nil, \nil$ aceita.
- De $a$:
- $q_I, a, \nil \trf{\nil, \nil/S} q, a, S \trf{\nil, S/\nil} q, a, \nil$. não aceita.
- $q_I, a, \nil \trf{\nil, \nil/S} q, a, S \trf{\nil, S/aSb} q, a, aSb \trf{a, a/\nil} q, \nil, Sb \trf{\nil, S/\nil} q, \nil, b$. não aceita.
- $q_I, a, \nil \trf{\nil, \nil/S} q, a, S \trf{\nil, S/aSb} q, a, aSb \trf{a, a/\nil} q, \nil, Sb \trf{\nil, S/aSb} q, \nil, aSbb$. não aceita.
- Não há mais computações de $a$, que é rejeitada.
- De $ab$: $q_I, ab, \nil \trf{\nil, \nil/S} q, ab, S \trf{\nil, S/aSb} q, ab, aSb \trf{a, a/\nil} q, b, Sb \trf{\nil, S/\nil} q, b, b \trf{b, b/\nil} q, \nil, \nil$ aceita.
A derivação de uma palavra na GIC é replicada na computação do AP.
Por exemplo, a palavra $ab$ tem a seguinte derivação: $$S \nder{S \to aSb} aSb \nder{S \to \nil} ab$$ A mesma palavra tem a seguinte computação: $$q_I, ab, \nil \trf{\nil, \nil/S} q, ab, S \trf{\boxed{\nil, S/aSb}} q, ab, aSb \trf{a, a/\nil} q, b, Sb \trf{\boxed{\nil, S/\nil}} q, b, b \trf{b, b/\nil} q, \nil, \nil$$
Hierarquia de Chomsky
As GIC não são o único tipo de gramática:
- Tipo 0 ou sem restrições as produções são da forma $p \to q$ em que $p \in \del{V \cup \Sigma}^+$ e $q \in \clpar{V \cup \Sigma}$. Isto é, o lado esquerdo pode ser qualquer palavra não vazia. A substituição de um símbolo depende da “vizinhança” desse símbolo, o seu contexto.
- Tipo 1 ou dependente de contexto são como as de tipo 0 mas $\len{p} \leq \len{q}$. Tal como no Tipo 0 a substituição de símbolos depende do contexto mas, adicionalmente, as substituições contraem a palavra.
- Tipo 2 ou independente de contexto são as gramáticas usadas aqui. A substituição de um símbolo não depende do contexto em que este ocorre.
- Tipo 3 ou regular impõe ainda mais restrições às produções e geram as linguagens regulares.
Conclusão
Os AP são um modelo computacional das GIC. Especificamente, há um algoritmo que transforma uma GIC num AP equivalente. Além disso, as derivações na GIC são replicadas pelas computações do AP.
Ficam assim resolvidas as questões da adequação e da computação no Problema Principal de ALP — Dada uma linguagem $A$ e uma palavra $p$ no mesmo alfabeto, determinar se $p \in A$.
Falta ainda tratar da eficiência. Os AP não são deterministas e, ao contrário dos AFND, não se conhece nenhuma simulação determinista que seja geral e eficiente. A esperança que resta é condicionar as gramáticas de forma a que os AP associados sejam, em termos práticos, deterministas mas sem estragar a “capacidade expressiva” das gramáticas.
O próximo capítulo começa por visitar os principais tipos de Análise Sintática (o termo técnico do Principal Problema de ALP) e segue para métodos e tipos de gramáticas adequados à sua resolução eficiente.
Exercícios — Gramáticas e Autómatos de Pilha
Os exercícios assinalados com “✓” serão resolvidos nas aulas práticas; Os assinalados com “†” têm elevada dificuldade. Todos os restantes devem ser resolvidos pelos alunos.
Gramáticas Independentes do Contexto
Exercício 01
Escolha três ou quatro linguagens de programação (como C, python, Java
ou outras mais recentes como go ou swift) ou apenas formais (como o
XML) e encontre (online) gramáticas que as definam.
Exercício 02
Defina uma gramática independente do contexto que gere a linguagem:
- $\set{wcw^{R} \st w \in \set{a,b}\AST}$.
- $\set{wc^n \st w \in \set{a,b}\AST \text{\ e\ } n=\len{w}}$.
- $\set{a^i b^j c^k \st k \geq 0 \text{\ e\ } i+j=k}$.
- ✓ $\set{a^n b^m \st m,n \geq 0 \text{\ e\ } m \not= n}$.
- dos números naturais sem zeros não significativos.
Exercício 03
Defina uma gramática independente do contexto que gere os reais (incluindo os negativos) em que: a parte inteira é não vazia e não tem zeros não significativos; a parte decimal é não vazia e só termina em zero se for constituída por um único 0; e as partes inteira e decimal são separadas por uma vírgula.
Exercício 04
✓ Seja $L$ a linguagem de todas sequências de parêntesis, curvos - ‘$($’ e ‘$)$’ - e rectos - ‘$\lbrack$’ e ‘$\rbrack$’ -, bem emparelhados. Pertencem a esta linguagem palavras como $\nil$, “$()$”, “$\lbrack\rbrack$”, “$()\lbrack()\rbrack$”, “$(\lbrack()\rbrack)$” e “$(\lbrack\rbrack\lbrack(\lbrack\rbrack)\rbrack)\lbrack\rbrack$”. Não pertencem a $L$ palavras como “$\rbrack$”, “$($”, “$(\rbrack$”, “$(\lbrack)\rbrack$”, “$)($” e “$\lbrack()\rbrack\rbrack$”.
- Mostre que $L$ não é regular;
- Defina uma gramática independente do contexto que gere $L$.
Exercício 05
✓ Considere um conjunto $V$ de variáveis e um conjunto $F$ de símbolos de função, cada um com uma aridade maior que ou igual a zero. Um termo é definido como:
- uma variável é um termo.
- um símbolo de função de aridade 0 é um termo.1
- se $t_1, t_2, \ldots, t_k, k > 0$ são termos, então, para todos os símbolos de função $f$ de aridade $k$, $f\at{t_1, t_2, \ldots, t_k}$ é um termo;
- nada mais é um termo.
Defina uma gramática independente do contexto que gere os termos descritos — use os símbolos $v$ e $f$ como representantes das variáveis e dos símbolos de função, respetivamente. Exemplos de termos são $v$, $f$, $f(v)$ e $f(v,f(f(f),f))$.
Exercício 06
Considere a gramática $G = \del{\set{A}, \set{a,b}, \set{A \to AA \alt aAb \alt \nil}, A}$.
- Construa uma derivação esquerda para a palavra $aababb$ e a respetiva árvore de derivação.
- Construa uma derivação direita para a palavra $ababab$ e a respetiva árvore de derivação.
- Determine se G é ambígua. † Em caso afirmativo, apresente uma gramática não ambígua equivalente.
Exercício 07
✓ Considere a gramática independente do contexto $$G = \del{\set{S}, \set{a}, \set{S \to aa \alt SS}, S}.$$
- Mostre que esta gramática é ambígua.
- † Apresente uma gramática equivalente não ambígua.
- Apresente uma gramática regular equivalente.
- Apresente uma expressão regular que represente a linguagem gerada pela gramática.
Exercício 08
Resolva o exercício anterior para a gramática $$G = \del{\set{S,A}, \set{a}, \set{S \to \nil \alt AS, A \to \nil \alt a}, S}.$$
Exercício 09
Defina uma gramática livre do contexto que gere a linguagem …
- $\set{0^{2k}1^{k-1} \st k\geq 1}$. Usando essa gramática, derive a palavra $00001$.
- $\set{1^{2k+1}0^{k} \st k\geq 0}$. Usando essa gramática, derive a palavra $1110$.
Exercício 10
† Defina uma gramática livre do contexto que gere todas a expressões regulares sobre o alfabeto $\set{a,b}$.
Exercício 11
Considere a gramática livre do contexto $S\to aSaa \alt B; B\to bbBcc \alt C; C\to bc$
- Derive $a^3b^3c^3a^6$.
- † Mostre que esta gramática é não ambígua.
Exercício 12
Considere a gramática livre do contexto $S\to AaSbB \alt \nil; A\to aA \alt a; B\to bB \alt \nil$;
- Mostre que esta gramática é ambígua.
- Encontre uma gramática equivalente, não ambígua.
Autómatos de Pilha
Exercício 13
✓ Defina um autómato finito que reconheça a linguagem gerada pela gramática $S \to 01S | 0S | 11 | 1$.
Exercício 14
✓ Defina um autómato de pilha que reconheça a linguagem $\set{w \st w \in \set{a,b}\AST \text{\ e\ } w = w^{R}}$. Será possível definir um autómato de pilha determinista que reconheça esta linguagem? Justifique a sua resposta.
Exercício 15
✓ Considere a linguagem de todas as palavras sobre $\set{a,b}$ em que o número de $a$ é igual ao número de $b$:
$$\set{p \in \set{a, b}\AST \st \len{p}_a = \len{p}_b}$$
- defina um autómato de pilha não determinista que a reconheça.
- † defina um autómato de pilha determinista que a reconheça.
Exercício 16
Defina um autómato de pilha que reconheça $L = \set{1^n + 1^m = 1^{m+n} \st n,m \geq 0}$ e indique se esse autómato é, ou não, determinista.
Exercício 17
Defina um autómato de pilha que reconheça $L = \set{a^{2n}b^{3n} \st n \geq 0}$.
Exercício 18
Construa um autómato de pilha que reconheça a linguagem das expressões aritméticas com o operador $+$ e com parêntesis. Use o símbolo $n$ para representar os operandos atómicos, i.e., as expressões terão o seguinte aspeto: $n$, $n+n$, $(n+(n+(n)))+n$, etc.
Implementação
 |
|---|
As indicações gerais para os exercícios de implementação são válidas aqui.
Uma biblioteca para GIC e AP
Para esta biblioteca são adotadas as seguintes convenções e orientações:
- Um símbolo é uma
stringválida: umastringnão vazia em que não ocorre' '. - Uma variável é um símbolo que começa por uma maiúscula.
- Um terminal é um símbolo que não é uma variável.
- Estão implementadas funções
is_symbol(s),is_variable(s)eis_terminal(s). - Uma palavra é uma lista de símbolos.
- As regras são representadas pela classe
Rule, com:- O construtor
Rule(var, word). - Os métodos básicos
variables(),terminals(),equals(other). - Os métodos analíticos
is_nil(),is_recursive(),is_wellformed(). - Os métodos operacionais
dderive_left(word),dderive_right(word). - O método auxiliar
__repr__()com “→” para a seta e usando “λ” quando adequado. - A função auxiliar
parse_grammar(s). Assume-se quesé umastringcom os símbolos separados por espaços, que o primeiro desses símbolos define o lado esquerdo da regra e os restantes a palavra do lado direito. Por exemplo,"A a A b"define a regraA→aAb.
- O construtor
- As gramáticas são representadas pela classe
Grammar, com:- O construtor
Grammar(rules). - Os métodos básicos
variables(),terminals(),rules_of(symbol)eset_start(symbol). - Os métodos analíticos
is_wellformed(),start()(o símbolo inicial),is_nil(symbol),nil_symbols(),is_recursive(symbol),recursive_symbols(). - Os métodos operacionais
derive_left(sequence, word),derive_right(sequence, word)ondesequenceé uma lista com indíces das regras ewordé um parâmetro opcional com valor por omissão igual ao símbolo inicial da gramática (start()). - O método auxiliar
__repr__(). - A função auxiliar
parse_grammar(s). Assume-se quesé umastringcom blocos de regras separados por';'e em que cada bloco de regras é da formaV : P1 | P2 | ...| Pn. Por exemplo"S:a A b|;A:S|c"define a gramática $S \to aAb \ |\ \nil; A \to S\ |\ c$. Note bem que as regras de uma variável podem estar “espalhadas” por vários blocos e que eventuais repetições de regras devem ser descartadas.
- O construtor
- O símbolo inicial (
start) de uma gramática é calculado da seguinte forma:- Se for usado o método
set_start(symbol)é o valor do parâmetrosymbol. - Caso contrário, se
'S'é uma variável na gramática ou se a gramática tem zero regras, o símbolo inicial é'S'. - Por fim, se nenhuma das outras situações se verifica, é o lado esquerdo da primeira regra da gramática.
- Se for usado o método
- As linhas das transições, $(q_1, s_1) \in \delta(q_0, a, s_0)$, são representadas pela classe
TrLine, com:- O construtor
TrLine(state_0, symbol, stack_0, state_1, stack_1)onde(state_0, symbol, stack_0, state_1, stack_1)é $(q_0, a, s_0, q_1, s_1)$.
- O construtor
- As configurações, $(q, p, s)$, são representadas pela classe
Configuration, com:- O construtor
Configuration(state, tape, stack)onde(state, tape, stack)é $(q, p, s)$. - Os métodos analíticos
is_final(final_symbols),is_fitting(trline)eall_fitting(transition). - Os métodos operacionais
next(trline, check)etree(delta, max_depth, check)em quechecké um parâmetro opcional que por omissão valeFalsee, sendo verdadeiro, ativa a verificaçãois_fitting(trline). Note bem que o resultado de aplicar uma linha a uma configuração incompatível é a configuração inicial.
- O construtor
Exercício 19
Sempre que possível teste a sua biblioteca com as gramáticas e os autómatos dos exercícios anteriores.
Análise Sintática
 |
A Análise Sintática trata de relacionar uma palavra com uma gramática. Especificamente, pretende-se saber se a palavra é gerada pela gramática e, se sim, qual a sua derivação.
Portanto,
A Análise Sintática é uma versão do Problema Principal de ALP quando a linguagem é gerada por uma GIC.
No capítulo anterior definiram-se as gramáticas independentes de contexto e os autómatos de pilha, para ultrapassar os limites das linguagens regulares e dos autómatos finitos no que diz respeito à definição de linguagens de programação.
Ficaram assim resolvidas as necessidades sobre um esquema formal adequado para representar as linguagens de programação e dum modelo de computação para determinar se $p \in L\at{G}$.
Mas mantém-se o problema da eficiência porque, embora os autómatos de pilha proporcionem um modelo computacional para as linguagens independentes de contexto, não se conhecem formas gerais para garantir que as suas computações sejam eficientes.
Restam duas possibilidades: Ou condicionar as gramáticas de forma a reduzir a ramificação durante as derivações ou “espreitar” os símbolos por processar para “guiar” as computações,
Este capítulo começa por visitar os principais métodos de pesquisa geral em grafos, de forma a avaliar o problema da eficiência nalguns casos concretos.
De seguida é primeiro apresentado um processo (sequência de passos) que permite transformar uma GIC noutra equivalente e melhor adaptada ao algoritmos de pesquisa geral (a Forma Normal de Greibach). Por fim são apresentadas as classes de gramáticas $LL$ e $LR$, que “espreitam” os próximos símbolos “por processar” para definir algoritmos deterministas de análise sintática.
Análise Sintática
Pesquisar o Grafo de uma GIC ou uma Árvore das Computações de um AP de forma a encontrar a derivação de uma palavra e construir uma árvore de sintaxe abstrata.
Introdução
A eficiência computacional da análise sintática tem um problema, manifesto no não determinismo dos autómatos de pilha (que, ao contrário dos AFND, deles não se conhece nenhuma simulação determinista, geral e eficiente) e, equivalentemente, nas múltiplas produções das gramáticas independentes do contexto. Ambos estes casos têm representações gráficas: o Grafo da Gramática nas GIC e as Árvores das Computações nos AP.
Nesta situação é necessário fazerem-se pesquisas, abrangendo (no pior cenário) todas as possibilidades. Este é um processo inerentemente (demasiado) demorado pelo que importa encontrar formas de o melhorar.
Conteúdo
Do Problema Principal de ALP — Dada uma linguagem $L \subseteq \cl{\Sigma}$ e uma palavra $p \in \cl{\Sigma}$, determinar se $p \in L$. resta resolver a questão da eficiência computacional, já que a adequação ficou resolvida com as GIC e a computação com os AP.
Intuitivamente, para determinar se $p \in L$ usando um AP, $A$, é necessário explorar a árvore das computações de $A$ com entrada $p$. Especificamente:
O problema de determinar se $p \in L\at{G}$ pode ser resolvido por pesquisa na árvore das computações do AP $A$.
Além disso, como os AP e as GIG são equivalentes, esta observação também sugere que
As derivações de uma GIC podem ser representadas por um grafo orientado.
Mais abaixo vai ser definida rigorosamente a representação das derivações da GIC por um grafo e como é que o problema $p \in L$ pode ser resolvido por pesquisa quer no grafo (das derivações) da GIC quer no grafo (das computações) do AP.
Entretanto, interessa fazer uma breve revisão sobre pesquisa em grafos orientados. O problema pode ser definido como:
Pesquisa em Grafos Orientados. Dado um grafo orientado, descobrir se existe algum caminho $v_0 \to v_1 \to \cdots \to v_n$ desde um vértice inicial, $v_0$, até um vértice final, $v_n$.
A resolução geral deste problema segue o seguinte código:
def pesquisa(grafo, a, b):
candidatos = [ a ]
visitados = []
while len(candidatos) > 0:
candidato = candidatos.pop(0)
visitados.append(candidato)
if candidato == b:
return True
else:
proximos = expande(grafo, candidato)
proximos_novos = remove(proximos, visitados)
candidatos = junta(candidatos, proximos_novos)
return False
N.B. Este código é muito geral e, portanto, não otimizado. Melhorias significativas podem incluir, por exemplo, um resuldado mais descritivo, com o caminho de a até b.
Há quatro variantes da resolução geral deste problema, que correspondem às combinações da seguintes opções para expande e para junta:
- Se
expande(G, v)segue a direção das arestas — devolve os filhos devemG— a pesquisa é descendente, coma = inicialeb = final. - Se
expande(G, v)segue contra a direção das arestas — devolve os pais devemG— a pesquisa é ascendente, coma = finaleb = inicial. - Se
junta(x, y)devolvex + y(xseguido dey) — a pesquisa é em largura. - Se
junta(x, y)devolvey + x(yseguido dex) — a pesquisa é em profundidade.
Resumidamente:
a | b | expande | junta(x, y) | Pesquisa |
|---|---|---|---|---|
| $v_0$ | $v_n$ | filhos | y + x | Descendente Profundidade |
| $v_0$ | $v_n$ | filhos | x + y | Descendente Largura |
| $v_n$ | $v_0$ | pais | y + x | Ascendente Profundidade |
| $v_n$ | $v_0$ | pais | x + y | Ascendente Largura |
A função remove exclui dos candidatos os vértices já visitados e não depende do tipo de pesquisa.
Grafo de uma Gramática
Todas as possíveis derivações de uma gramática podem ser organizadas num grafo orientado, que começa no símbolo inicial e “percorre” sucessivamente as produções aplicadas durante as derivações. Neste grafo “caminhos” diferentes representam derivações diferentes. Os vértices “são” as palavras intermédias e as arestas as produções aplicadas:
Grafo Esquerdo (resp. Direito) de uma GIC. Seja $G=\del{V, \Sigma, P, S}$ uma GIC. O grafo esquerdo de $G$ (resp. direito) é o digrafo com:
- Vértices: as palavras do conjunto $N = \set{p \in \clpar{V \cup \Sigma} \st S \iderL p}$ (resp. $S \iderR p$).
- Arestas: os elementos de $A = \set{\del{a,b,p} \in N \times N \times P \st a \nderL{p} b}$ (resp. $a \nderR{p} b$).
Por exemplo, para a GIC $S \to aS \alt \nil$ parte do grafo esquerdo é
| Grafo Esquerdo de $S \to aS \alt \nil$ (parcial) |
|---|
 |
O grafo (esquerdo/direito) de uma GIC representa todas as possíveis derivações (esquerdas/direitas) dessa GIC. Este grafo não tem de ser uma árvore porque no grafo de uma gramática ambígua há vários “caminhos” para o mesmo vértice.
Exemplo/Exercício: Desenhe o grafo de $S \to aS \alt Sa \alt \nil $.
As árvores e as gramáticas não ambíguas estão relacionadas:
O grafo esquerdo (resp. direito) de uma GIC não ambígua é uma árvore. Recíprocamente, se o grafo esquerdo (resp. direito) de uma GIC for uma árvore, então a GIC é não ambígua.
O grafo da GIC não deve ser confundido com as árvores de derivação, que ilustram uma possível derivação de uma palavra.
Qualquer palavra de terminais gerada pela GIC é um vértice sem filhos. Isto é, $G \ider p \in \cl{\Sigma}$ se, e só se, $p$ é um vértice sem filhos no grafo de $G$.
Isto é a reformulação do Problema Principal de ALP como um problema de pesquisa em grafos: Dada uma GIC $G = \del{V, \Sigma, P, S}$ e uma palavra $p \in \cl{\Sigma}$, existe algum caminho $S \longrightarrow p$ no grafo (esquerdo) de $G$? Nesse caso $p \in L\at{G}$; caso contrário $p \not\in L\at{G}$.
Exemplos com Expressões Algébricas Simplificadas
Para ilustrar melhor os grafos esquerdos e direitos, assim como os algoritmos de pesquisa, considere-se a seguinte gramática, para expressões algébricas simplificadas (EAS):
$$ \mathrm{EAS}: \left\lbrace \begin{aligned} S &\to U \alt S + U \cr U &\to a \alt b \end{aligned} \right. $$
Os inícios dos grafos (esquerdo e direito) são
| Grafo Esquerdo de EAS | Grafo Direito de EAS |
|---|---|
 |  |
Portanto, para já, a análise sintática pode ser feita em oito tipos de pesquisa:
| Direção | Estratégia | Grafo |
|---|---|---|
| Descendente | Largura | Grafo da GIC |
| Descendente | Largura | Árvore das Computações do AP |
| Descendente | Profundidade | Grafo da GIC |
| Descendente | Profundidade | Árvore das Computações do AP |
| Ascendente | Largura | Grafo da GIC |
| Ascendente | Largura | Árvore das Computações do AP |
| Ascendente | Profundidade | Grafo da GIC |
| Ascendente | Profundidade | Árvore das Computações do AP |
Análise Sintática Descendente em Largura no Grafo da GIC
Intuitivamente, mantém-se uma lista de candidatos, iniciada com $S$ e aplicam-se sucessivamente produções, sempre ao primeiro elemento dessa lista, o “candidato”. Há três hipóteses:
- O candidato é o alvo ou não há candidatos. A pesquisa termina.
- O candidato é incompatível com o alvo. Passa-se ao próximo candidato.
- O candidato é compatível com o alvo, mas diferente. Os filhos do candidato atual são acrescentados ao fim da lista.
Compatível significa que o prefixo terminal do candidato é um prefixo do alvo.
Por exemplo, nas EAS, a pesquisa DL de $b+a$ é:
$$ \begin{aligned} S \cr U &,& S + U \cr S + U &,& a, b \cr a &,& b, U + U, S + U + U \cr b &,& U + U, S + U + U \cr U + U &,& S + U + U \cr S + U + U &,& a + U, b + U \cr a + U &,& b + U, U + U + U, S + U + U + U \cr b + U &,& U + U + U, S + U + U + U, a + a, a + b \cr U + U + U &,& S + U + U + U, a + a, a + b, b + a, b + b \cr \vdots \cr b + a &,& \cdots \end{aligned} $$
Análise Sintática Descendente em Profundidade no Grafo da GIC
Intuitivamente, mantém-se uma lista de candidatos, iniciada com $S$ e aplicam-se sucessivamente produções, sempre ao primeiro elemento dessa lista, o “candidato”. Há três hipóteses:
- O candidato é o alvo ou não há candidatos. A pesquisa termina.
- O candidato é incompatível com o alvo. Passa-se ao próximo candidato.
- O candidato é compatível com o alvo, mas diferente. Os filhos do candidato atual são acrescentados ao início da lista.
Por exemplo, nas EAS, a pesquisa DP de $b+a$ é:
$$ \begin{aligned} S \cr U &,& S + U \cr a&,& b, S + U\cr b &,& S + U \cr S + U\cr U + U &,& S + U + U \cr a + U &,& b + U, S + U + U \cr b + U &,& S + U + U \cr b + a &,& b + b, S + U + U \end{aligned} $$
Análise Sintática Ascendente e as Computações do AP
As pesquisas anteriores percorrem o grafo da gramática, gerado pelas suas produções. Por outro lado, os autómatos de pilha, sendo equivalentes às GIC, também podem ser usados para a análise sintática.
No caso dos AP o não determinismo ocorre sempre que uma configuração tem dois ou mais sucessores. Por outro lado a própria palavra proporciona informação que pode ser usada para guiar a pesquisa.
As computações nos AP “consomem” a palavra na entrada e este processo é semelhante às pesquisas ascendentes, que começam no “alvo” e “andam para trás” até chegarem a um vértice “inicial”.
O processo de pesquisa nas computações é essencialmente descrito pelas operações de transferência e de redução de um certo AP derivado da GIC.
N.B. que este AP não foi ainda formalmente definido.
Intuitivamente, a palavra da entrada é passada para a pilha, transferindo um símbolo de cada vez. Também a palavra que está na pilha pode ser reduzida, isto é, “desfeito” o resultado de aplicar uma produção. No fim, a entrada deve ficar vazia e a pilha só com o símbolo inicial.
Redução é o inverso da aplicação de uma produção. Por exemplo, se $A \to cBc$ for uma produção então uma possível redução da palavra $bbcBcab$ será $bbAab$ porque $bb\underline{A}ab\nder{A \to cBc} bb\underline{cBc}ab$.
Por exemplo, escolhendo convenientemente as operações “transferência”, $Tr$, da entrada para a pilha e “redução”, $Red$, duma subpalavra na pilha, uma computação possível de $b+a$ é
$$ \begin{array}{lr|cl} \text{pilha} & \text{entrada} & \text{operação} & \text{produção} \cr \hline \nil & b + a & Tr\cr b & + a & Red& U \to b \cr U & + a & Red & S \to U \cr S & + a & Tr \cr S + & a & Tr \cr S + a &\nil& Red & U \to a \cr S + U &\nil& Red & S \to S + U \cr S & \nil \end{array} $$
Um resultado interessante deste método é que as reduções aplicadas mostram uma derivação direita da palavra, lida “de baixo para cima” na coluna “Produção”:
$$S \nder{S \to S + U} S + U \nder{U \to a} S + a \nder{S \to U} U + a \nder{U \to b} b + a$$
Este esquema não só determina se a palavra é gerada pela gramática como, nesse caso, encontra uma derivação da palavra.
No entanto, tem algumas fontes de não determinismo:
- Quando fazer uma redução ou uma transferência?
- Numa redução podem ser escolhidos várias subpalavras da pilha e várias produções da gramática.
Por exemplo, dada a GIC $S \to aA \alt bB, A \to a, B \to aa \alt a$ como reduzir $baa$ na pilha? Pode escolher-se:
| Subpalavra | Produção | Nova Pilha |
|---|---|---|
| $ba\underline{a}$ | $A \to a$ | $baA$ |
| $ba\underline{a}$ | $B \to a$ | $baB$ |
| $b\underline{a}a$ | $A \to a$ | $bAa$ |
| $b\underline{a}a$ | $B \to a$ | $bBa$ |
| $b\underline{aa}$ | $B \to aa$ | $bB$ |
Análise Sintática Ascendente em Largura
Intuitivamente, mantém-se uma lista de candidatos, iniciada com $p$ e aplicam-se todas as reduções possíveis, sempre ao primeiro elemento dessa lista, o “candidato”. Há duas hipóteses:
- O candidato é a produção inicial ou não há candidatos. A pesquisa termina.
- O candidato admite reduções. Os pais desse candidato são acrescentados ao fim da lista.
Por exemplo, nas EAS, a pesquisa AL de $b+a$ é:
$$ \begin{aligned} b + a \cr U + a &,& b + U \cr b + U &,& S + a, U + U \cr S + a &,& U + U, b + S, (U + U) \cr U + U &,& b + S, S + U \cr b + S &,& S + U, U + S, (S + U) \cr S + U &,& U + S, (U + S) \cr U + S &,& S, S + S \cr S &,& S + S, (S + S) \end{aligned} $$
Análise Sintática Ascendente em Profundidade
Intuitivamente, mantém-se uma lista de candidatos, iniciada com $p$ e aplicam-se todas as reduções possíveis, sempre ao primeiro elemento dessa lista, o “candidato”. Há duas hipóteses:
- O candidato é a produção inicial ou não há candidatos. A pesquisa termina.
- O candidato admite reduções. Os pais do candidato atual são acrescentados ao início da lista.
Por exemplo, nas EAS, a pesquisa AP de $b+a$ é:
$$ \begin{aligned} b + a \cr U + a &,& b + U \cr S + a&,& U + U, b + U\cr S + U&,& U + U, b + U\cr S&,& U + U, b + U\cr \end{aligned} $$
Conclusão
Depois de resolvidas as questões da adequação e da computação, está-se a tratar da eficiência no Problema Principal de ALP/Análise Sintática.
A análise sintática é representada como um problema de pesquisa em grafos orientados que, em geral, pode ser resolvido por quatro estratégias diferentes:
(ascendente ou descendente) x (largura ou profundidade). Por outro lado a pesquisa tanto pode ser feita no grafo da gramática como na árvore das computações do autómato de pilha.
Nenhuma destas estratégias gerais é eficiente. Para melhorar este problema e guiar as pesquisas na análise sintática colocam-se duas possibilidades: ou se condiciona a gramática, de forma reduzir as produções aplicáveis em cada passo ou, então, consultam-se os símbolos por processar para guiar as transições dos autómatos de pilha.
Formas Normais
Gramáticas Adaptadas para Análise Sintática por Pesquisa Geral.
Introdução
A análise sintática é representada como um problema de pesquisa em grafos orientados que, em geral, pode ser resolvido por quatro estratégias diferentes: (ascendente ou descendente) x (largura ou profundidade). Nenhuma destas estratégias gerais é eficiente.
Nesta secção é apresentado um processo (a normalização de uma gramática) que, numa sequência de passos, transforma numa gramática noutra, equivalente, e adaptada (tanto quanto possível) aos algoritmos de pesquisa: uma forma normal.
Conteúdo
O bom funcionamento (mínimo número de passos) da pesquisa no grafo de uma GIC depende da própria gramática.
Problemas como:
- Pesquisas infinitas quando a palavra não é derivada pela gramática.
- Exploração repetida de ramos quando a gramática é ambígua.
reduzem significativamente o desempenho da pesquisa.
Em certos caso é possível transformar a gramática dada noutra equivalente mas que “favorece” a pesquisa, reduzindo o número de ramificações, desambiguando, e/ou detetando “cedo” se a palavra não é gerada pela gramática.
Esta secção descreve um processo algorítmico de transformação de gramáticas. No fim a gramática que se obtém proporciona pesquisas gerais mais eficientes.
Todo este processo vai ser ilustrado com um exemplo de uma GIC (especialmente desenhada) para ilustrar a aplicação de cada passo:
$$ \begin{aligned} G^0 =& \del{\set{L, M, N, O}, \set{a, b, c, d}, \ldots, L} \cr &\begin{aligned} L &\to Mb \alt aLb \alt \nil \cr M &\to Lb \alt MLN \alt \nil \cr N &\to NaN \alt NbO \cr O &\to cO \alt \nil \end{aligned} \end{aligned} $$
1. Símbolo Inicial Não Recursivo
A recursividade é a “vantagem” das GIC sobre as ER, mas é também, uma fonte de dificuldades. Embora não seja desejável, nem sequer possível, remover completamente a recursividade das produções de uma GIC esta pode ser, em certos casos, controlada.
Símbolo Inicial Não Recursivo. Seja $G = \del{V, \Sigma, P, S}$ uma GIC. Existe uma GIC $G’ = \del{V’, \Sigma, P’, S’}$ equivalente a $G$ e onde o símbolo inicial não é recursivo.
Porque:
- Se o símbolo inicial de $G$ não for recursivo então $G’ = G$.
- Se o símbolo inicial de $G$ for recursivo então, fazendo $S’$ uma variável nova:
$$ G’ = \del{V \cup \set{S’}, \Sigma, P \cup \set{S’ \to S}, S’}. $$
Exemplo. Em $G^0$ o símbolo inicial é recursivo porque $L \to aLb$ é uma produção de $G^0$. Portanto esta gramática é transformada em
$$ \begin{aligned} G^1 =& \del{\set{\alert{L’}, L, M, N, O}, \set{a, b, c, d}, \ldots, \alert{L’}} \cr & \begin{aligned} \alert{L’} &\alert{\to L} \cr L &\to Mb \alt aLb \alt \nil \cr M &\to Lb \alt MLN \alt \nil \cr N &\to NaN \alt NbO \cr O &\to cO \alt \nil \end{aligned} \end{aligned} $$
Em $G^1$ o símbolo inicial já não é recursivo. Além disso, $L\at{G^0} = L\at{G^1}$.
2. Eliminação de Produções Vazias
Antes de tratar do segundo passo na normalização de uma gramática é necessário definir alguns conceitos e técnicas.
Quase todas as produções “aumentam” o tamanho da palavra. Por exemplo $A \to bB$ faz com que $aAa$ passe para $abBa$, isto é de comprimento três para quatro. E esta é uma propriedade desejável pois permite cortar “filhos demasiado grandes” durante a pesquisa.
Há duas exceções de nota: as produções vazias $A \to \nil$ e as produções unitárias $A \to B$. Formalmente:
Produções Vazias. Produções Unitárias. Gramática Contraível. Seja $G = \del{V, \Sigma, P, S}$ uma GIC.
- Uma produção vazia tem a forma $A \to \nil$.
- Uma produção unitária tem a forma $A \to B$.
- O conjunto dos geradores da palavra vazia é $$\Lambda = \set{A \in V \st A \ider \nil}.$$
- Numa gramática não contraível não existem geradores da palavra vazia. Isto é $\Lambda = \empty$.
- Numa gramática essencialmente não contraível o único gerador de vazio é o símbolo inicial. Isto é $\Lambda = \set{S}$.
O interesse das gramáticas essencialmente não contraíveis é que:
Numa gramática essencialmente não contraível os passos intermédios de uma derivação só podem diminuir de tamanho por aplicação de $S \to \nil$.
Não é possível, nem desejável, descartar completamente os geradores de vazio. Por exemplo, se $\nil \in L\at{G}$ então em qualquer gramática equivalente a $G$ tem de existir pelo menos uma produção vazia. Neste caso, o melhor que se pode fazer é “concentrar” todas as produções vazias em $S \to \nil$.
A transformação de uma gramática noutra equivalente envolve a introdução de novas produções e a substituição de uma produção por outras, de forma a manter a linguagem gerada.
Introdução de Produções. Substituição de Produções. Seja $G = \del{V, \Sigma, P, S}$ uma CIG.
- Se $A \ider u$ então $G’ = \del{V, \Sigma, P \cup \set{A \to u}, S}$ é equivalente a $G$.
- Se $A \to uBv \in P$ e $B \to w_1 \alt w_2 \alt \cdots \alt w_n$ são todas as produções de $B$ então a gramática $G’ = \del{V, \Sigma, P’, S}$ em que $$P’ = P \setminus \set{A \to uBv} \cup \set {A \to uw_1v \alt uw_2v \alt \cdots \alt uw_n v}$$ é equivalente a $G$.
Intuitivamente, estas duas regras permitem “saltar” passos intermédios numa derivação.
O primeiro passo para retirar as produções que reduzem o comprimento das palavras trata das produções vazias.
Eliminação de Produções Vazias. Sejam $G = \del{V, \Sigma, P, S}$ uma GIC em que o símbolo inicial não é recursivo. e $G’ = \del{V, \Sigma, P’, S}$ em que as produções são, em conjunto:
- As produções de $P$ que não são produções da palavra vazia.
- A produção $S \to \nil$ se $\nil \in L\at{G}$.
- Todas as produções que se obtêm eliminando um ou mais símbolos de $\Lambda$ do corpo $w$ de cada produção $A \to w$, desde que o resultado, $w’$, tenha pelo menos um símbolo.
Então $G’$ é equivalente a $G$ e essencialmente não contraível.
Exemplo. Na gramática $G^1$ o símbolo inicial não é recursivo. Além disso, os seus geradores da palavra vazia são $$ \Lambda = \set{L’, L, M, O}. $$
A gramática $G^2$, que resulta de $G^1$ por eliminação das produções vazias é:
$$ \begin{aligned} G^2 =& \del{\set{L’, L, M, N, O}, \set{a, b, c, d}, \ldots, L’} \cr & \begin{aligned} L’ & \to L \alt \alert{\nil} \cr L &\to Mb \alt \alert{b} \alt aLb \alt \alert{ab} \alt \xcancel{\nil} \cr M &\to Lb \alt \alert{b} \alt MLN \alt \alert{LN} \alt \alert{MN} \alt \alert{N} \alt \xcancel{\nil} \cr N &\to NaN \alt NbO \alt \alert{Nb}\cr O &\to cO \alt \alert{c} \alt \xcancel{\nil} \end{aligned} \end{aligned} $$
Note-se que:
- Foram retiradas as produções $L \to \nil$ e $M \to \nil$.
- Como $\nil \in L\at{G^1}$, foi acrescentada $L’ \to \nil$.
- De cada produção em cujo corpo ocorrem geradores da palavra vazia foram acrescentadas variantes sem esses símbolos. Por exemplo:
- Em $L \to Mb$ no corpo, $Mb$, ocorre $M \in \Lambda$. Portanto é acrescentada a produção $L \to b$, que resulta de $Mb$ removendo $M$.
- Mais interessante, no corpo da produção $M \to MLN$ tanto $M$ como $L$ são geradores da palavra vazia. As combinações possíveis sem algum desses elementos são $LN, MN, N$.
Sem os cálculos auxiliares:
$$ \begin{aligned} G^2 =& \del{\set{L’, L, M, N, O}, \set{a, b, c, d}, \ldots, L’} \cr & \begin{aligned} L’ & \to L \alt \nil \cr L &\to Mb \alt b \alt aLb \alt ab \cr M &\to Lb \alt b \alt MLN \alt LN \alt MN \alt N \cr N &\to NaN \alt NbO \alt Nb\cr O &\to cO \alt c \end{aligned} \end{aligned} $$
3. Eliminação de Produções Unitárias
As produções unitárias substituem uma variável por outra variável e podem ser eliminadas usando cadeias.
Cadeia. Seja $G = \del{V, \Sigma, P, S}$ uma GIC essencialmente não contraível.
Para cada $A \in V$, a cadeia de $A$ é o conjunto $\cadeia\at{A} = \set{B \in V \st A \ider B}$.
Qualquer gramática $G’ = \del{V, \Sigma, \ldots, S}$ cujas produções $A \to w$ são tais que:
- $w \not\in V$.
- Existe $B \in \cadeia\at{A}$ tal que $B \to w \in P$.
é equivalente a $G$.
Este enunciado pode ser difícil de interpretar. O primeiro ponto afirma que na gramática $G’$ não existem produções unitárias. O segundo ponto permite substituir a produção unitária $A \to B$ por $A \to w$ para cada $B \to w$.
Exemplo. As cadeias de $G^2$ são
$$ \begin{array}{l|l} A \in V & \cadeia\at{A} \cr \hline L’ & L’, L\cr L & L \cr M & M, N\cr N & N \cr O & O \end{array} $$
e as produções unitária são $L’ \to L$ e $M \to N$. As respetivas substituições são:
- de $L’ \to \alert{L}$, dado que $L \to Mb \alt b \alt aLb \alt ab$: $L’ \to \alert{Mb \alt b \alt aLb \alt ab}$.
- de $M \to \alert{N}$, dado que $N \to NaN \alt NbO \alt Nb$: $M \to \alert{NaN \alt NbO \alt Nb}$.
A gramática que se obtém, equivalente a $G^2$, é:
$$ \begin{aligned} G^3 =& \del{\set{L’, L, M, N, O}, \set{a, b, c, d}, \ldots, L’} \cr & \begin{aligned} L’ & \to Mb \alt b \alt aLb \alt ab \alt \nil \cr L &\to Mb \alt b \alt aLb \alt ab \cr M &\to Lb \alt b \alt MLN \alt LN \alt MN \alt NaN \alt NbO \alt Nb \cr N &\to NaN \alt NbO \alt Nb\cr O &\to cO \alt c \end{aligned} \end{aligned} $$
4. Eliminação de Símbolos Inúteis
A definição de linguagem gerada pela GIC $G = \del{V, \Sigma, P, S}$ é $$ L\at{G} = \set{p \in \cl{\Sigma} \st S \ider p} $$
Uma inspeção rápida a $N \to NaN \alt NbO \alt Nb$ mostra que a recursividade desta variável impede-a de gerar palavras só de terminais. Portanto, em termos de linguagem gerada, este é um símbolo que pode ser retirado da gramática. Também podem ser retirados os símbolos que não podem ser atingidos a partir do símbolo inicial.
Símbolo Útil. Símbolo Acessível. Gramática Limpa. Seja $G = \del{V, \Sigma, P, S}$ uma GIC.
Um símbolo $x \in V \cup \Sigma$ é:
- Útil se existe uma derivação $S \ider u\alert{x}v \ider p \in \cl{\Sigma}$.
- Inútil se não é útil.
- Acessível se existe uma derivação $S \ider u\alert{x}v$.
- Inacessível se não é acessível.
Uma variável $A \in V$ é:
- Produtiva se $A \ider p \in \cl{\Sigma}$.
- Improdutiva se não é produtiva.
Uma variável é útil se e só se for acessível e produtiva.
Uma gramática sem símbolos inúteis e inacessíveis diz-se limpa (ou reduzida).
Para limpar uma gramática de símbolos inúteis e inacessíveis:
- Eliminar as variáveis improdutivas:
- Encontrar as variáveis produtivas (por exemplo, derivando delas uma palavra só de terminais).
- Remover as produções onde ocorrem as variáveis improdutivas.
- Eliminar as variáveis inacessíveis:
- Encontrar os símbolos acessíveis (por exemplo, fazendo uma derivação a partir do símbolo inicial onde o símbolo ocorra).
- Remover as produções das variáveis inacessíveis.
Exemplo. Como foi observado acima, $N$ é inútil. Portanto as produções onde $N$ ocorre podem ser removidas. As novas produções são:
$$ \begin{aligned} L’ & \to Mb \alt b \alt aLb \alt ab \alt \nil \cr L &\to Mb \alt b \alt aLb \alt ab \cr M &\to Lb \alt b \alt \xcancel{MLN} \alt \xcancel{LN} \alt \xcancel{MN} \alt \xcancel{NaN} \alt \xcancel{NbO} \alt \xcancel{Nb} \cr \xcancel{N} &\xcancel{\to NaN \alt NbO \alt Nb}\cr O &\to cO \alt c \end{aligned} $$
Como resultado destas remoções $O$ deixou de ser acessível: Nenhuma derivação $L’ \ider \cdots$ “contém” $O$. Portanto, também as produções de $O$ podem ser removidas e o resultado é:
$$ \begin{aligned} G^4 =& \del{\set{L’, L, M}, \set{a, b}, \ldots, L’} \cr & \begin{aligned} L’ & \to Mb \alt b \alt aLb \alt ab \alt \nil \cr L &\to Mb \alt b \alt aLb \alt ab \cr M &\to Lb \alt b \end{aligned} \end{aligned} $$
Note-se que, removendo as produções de $O$, o terminal $c$ ficou inacessível, pelo que foi retirado de $\Sigma$, tal como $d$, que nunca constou nas produções.
Finalmente, é fácil de verificar que $L’, L$ e $M$ são produtivos e acessíveis. Também $a$ e $b$ são acessíveis.
Numa gramática limpa todos os símbolos “contam”. Além disso, e de se ter tratado das produções vazias e unitárias, pouco se fez para melhorar o processo de pesquisa no grafo da gramática. Para esse efeito é preciso “controlar a forma” das produções.
5. Forma Normal de Chomsky
O corpo das produções de uma CIG é uma palavra de $\clpar{V \cup \Sigma}$, pelo que pode ter vários terminais e variáveis misturados. Aqui pretende-se “arrumar” as formas possíveis que as produções podem ter.
Forma Normal de Chomsky (FNC). Uma GIC $G = \del{V, \Sigma, P, S}$ está na forma normal de Chomsky se cada uma das suas produções tem uma das formas seguintes:
- $A \to BC$ com $B, C \in V \setminus \set{S}$.
- $A \to a$ com $a \in \Sigma$.
- $S \to \nil$.
A forma normal de Chomsky é bastante fácil de obter, substituindo terminais “inconvenientes” por variáveis e usando novas variáveis para “agrupar” cadeias três ou mais símbolos.
Exemplo. Na gramática
$$ \begin{aligned} G^4 =& \del{\set{L’, L, M}, \set{a, b}, \ldots, L’} \cr & \begin{aligned} L’ & \to Mb \alt b \alt aLb \alt ab \alt \nil \cr L &\to Mb \alt b \alt aLb \alt ab \cr M &\to Lb \alt b \end{aligned} \end{aligned} $$
acrescentam-se $A \to a$ e $B \to b$ para retirar estes terminais das outras produções: $$ \begin{aligned} L’ & \to M\alert{B} \alt b \alt \alert{A}L\alert{B} \alt \alert{AB} \alt \nil \cr L &\to M\alert{B} \alt b \alt \alert{A}L\alert{B} \alt \alert{AB} \cr M &\to L\alert{B} \alt b \cr \alert{A} &\alert{\to a} \cr \alert{B} &\alert{\to b} \end{aligned} $$
Para se obter a FNC ainda falta tratar das produções $L’ \to ALB$ e $L \to ALB$. Para tal acrescenta-se a produção $X \to LB$ e substitui-se $L’, L \to AX$. O resultado final é:
$$ \begin{aligned} G^5 =& \del{\set{L’, L, M, \alert{A, B, X}}, \set{a, b}, \ldots, L’} \cr & \begin{aligned} L’ & \to MB \alt b \alt A\alert{X} \alt AB \alt \nil \cr L &\to MB \alt b \alt A\alert{X} \alt AB \cr M &\to LB \alt b \cr A &\to a \cr B &\to b \cr \alert{X} &\alert{\to LB} \end{aligned} \end{aligned} $$
6. Forma Normal de Greibach
Uma forma de reduzir o número de ramificações durante a pesquisa consiste em “olhar para o próximo símbolo” da palavra e escolher apenas produções que colocam esse símbolo no início.
Por exemplo, dadas a GIC $S \to aA \alt bB; A \to aA \alt \nil; B \to bB \alt \nil$ e a palavra $aa$, é simples de ver que a única derivação possível é $S \nder{S \to aA} aA \nder{A \to aA} aaA \nder{A \to \nil} aa$ porque em cada passo há só um candidato possível.
Neste caso, em cada passo da pesquisa é muito simples descartar todos os candidatos que não começam pelo terminal correto. Esta observação motiva a seguinte definição:
Forma Normal de Greibach (FNG). Uma GIC $G = \del{V, \Sigma, P, S}$ está na forma normal de Greibach se cada uma das suas produções tem uma das formas seguintes:
- $A \to aB_1 B_2 \cdots B_n$ com $a \in \Sigma, B_i \in V \setminus \set{S}, i \in 1\ldots n$.
- $A \to a$ com $a \in \Sigma$.
- $S \to \nil$.
Note-se que, em relação à forma normal de Chomsky, a única diferença na primeira forma das produções: $A \to aB_1 B_2 \cdots B_n$ em vez de $A \to BC$.
As gramáticas na FNG são úteis para:
- evitar recursões infinitas nos algoritmos de pesquisa.
- guiar (com o primeiro símbolo) a escolha das regras a expandir.
- produzir AP equivalente à gramática dada.
Construção de uma GIC na FNG
Ao contrário da construção da FNC, que é simples de obter, a construção de uma GIC na FNG requer alguma orientação.
Construção da FNG. Dada uma GIC $G = \del{V, \Sigma, P, S}$ na FNC:
- Ordenar as variáveis. Define-se uma ordem total nas variáveis de $G$ com uma única condição: $S$ é o primeiro elemento.
- Passo Descendente. Segue-se essa ordem para transformar todas as produções de modo que, se $\alert{A \to Bp}, B\in V, p \in \clpar{V\cup \Sigma}$ então $\alert{A \lt B}$.
- Passo Ascendente. Segue-se essa ordem invertida para substituir cada produção $\alert{A \to Bp}$ por $\alert{A \to qp}$ para cada produção $\alert{B \to q}, q \in \clpar{V\cup \Sigma}$.
Exemplo. Continuando com $G^5$, que está na FNC:
$$ \begin{aligned} L’ & \to MB \alt b \alt AX \alt AB \alt \nil \cr L &\to MB \alt b \alt AX \alt AB \cr M &\to LB \alt b \cr A &\to a \cr B &\to b \cr X &\to LB \end{aligned} $$
Ordenar as variáveis. A única condição é “$L’$ é o primeiro elemento”. Por exemplo $$L’ \lt X \lt B \lt A \lt L \lt M.$$
Passo Descendente. Ordenar as produções seguindo essa ordem.
$$ \begin{aligned} L’ & \to MB \alt b \alt AX \alt AB \alt \nil & L \lt M, A\cr X &\to LB & X < L\cr B &\to b \cr A &\to a \cr L &\to MB \alt b \alt \alert{A}X \alt \alert{A}B & L \lt M; \alert{L \not\lt A}\cr M &\to \alert{L}B \alt b & \alert{M \not\lt L} \end{aligned} $$
As produções de $L$ e de $M$ não verificam a condição do passo descendente. No caso de $L$ esse problema resolve-se facilmente substituindo o $A$ no início da produções de $L$ por $a$ (porque $A \to a$).
$$ \begin{aligned} L’ & \to MB \alt b \alt AX \alt AB \alt \nil & L \lt M, A\cr X &\to LB & X < L\cr B &\to b \cr A &\to a \cr L &\to MB \alt b \alt \underline{a}X \alt \underline{a}B & L \lt M\cr M &\to \alert{L}B \alt b & \alert{M \not\lt L} \end{aligned} $$
Resta o problema com a produção $ M \to \alert{L}B$. Segue-se também o método anterior:
$$ \begin{aligned} L’ & \to MB \alt b \alt AX \alt AB \alt \nil & L \lt M, A\cr X &\to LB & X < L\cr B &\to b \cr A &\to a \cr L &\to MB \alt b \alt aX \alt aB & L \lt M\cr M &\to \underline{\alert{M}B}B \alt \underline{b}B \alt \underline{aX}B \alt \underline{aB}B \alt b & \alert{M \not\lt M} \end{aligned} $$
Só que desta vez o problema não ficou resolvido e resultou numa Recursão Direta à Esquerda da variável $M$.
Eliminação da Recursividade Direta à Esquerda. Se
$$A \to A x_1 \alt \cdots \alt A x_n \alt y_1\alt \cdots \alt y_m$$
são as produções de $A$, organizadas de forma que:
- Cada $A x_1, \ldots, A x_n$ começa por $A$ e
- Nenhuma $y_1, \ldots, y_m$ começa por $A$.
Então obtém-se uma gramática equivalente:
- Acrescentando uma nova variável, por exemplo $Z$.
- Substituindo as produções de $A$ por
$$ \begin{aligned} A &\to y_1 Z \alt \cdots \alt y_m Z \alt y_1 \alt \cdots \alt y_m \cr Z &\to x_1 Z \alt \cdots \alt x_n Z \alt x_1 \alt \cdots \alt x_n \end{aligned} $$
Uma mnemónica para este processo é a seguinte:
Substituir $\alert{A \to A x \alt y}$ por $\alert{A \to yZ \alt y}$ e $\alert{Z \to xZ \alt x}$.
Intuitivamente percebe-se porque esta substituição é válida observando que a linguagem gerada por $A \to Ax \alt y$ é: $$ y, yx, yxx, yxxx, \ldots, yx^n, \ldots $$
Agora, outra forma de descrever esta linguagem é “Um $y$ seguido de zero ou mais $x$.” Neste caso:
- $Z \to xZ \alt x$ gera um ou mais $x$.
- $A \to yZ \alt y$ gera um $y$ seguido de zero ou um $Z$.
A eliminação da RDE de
$$ \overbrace{M}^{A} \to \overbrace{M}^{A}\ \overbrace{BB}^{x_1} \alt \overbrace{bB}^{y_1} \alt \overbrace{aXB}^{y_2} \alt \overbrace{aBB}^{y_3} \alt \overbrace{b}^{y_4} $$
define as produções
$$ \begin{aligned} M &\to bBZ \alt aXBZ \alt aBBZ \alt bZ &&\alt bB \alt aXB \alt aBB \alt b \cr Z &\to BBZ &&\alt BB \end{aligned} $$
pelo que a ordem inicialmente definida para as variáveis tem de ser estendida de forma que $Z < B$. Por exemplo:
$$L’ \lt X \lt \alert{Z} \lt B \lt A \lt L \lt M.$$
A nova gramática equivalente fica:
$$ \begin{aligned} L’ & \to MB \alt b \alt AX \alt AB \alt \nil & L \lt M, A\cr X &\to LB & X < L\cr \alert{Z} &\alert{\to BBZ \alt BB} & Z \lt B\cr B &\to b \cr A &\to a \cr L &\to MB \alt b \alt aX \alt aB & L \lt M\cr \alert{M} &\alert{\to bBZ \alt aXBZ \alt aBBZ \alt bZ \alt bB \alt aXB \alt aBB \alt b} \end{aligned} $$
No fim do passo descendente cada produção ou é vazia ou começa por um terminal ou começa por uma variável “mais abaixo”.
Passo Ascendente. Substituir, “de baixo para cima” a primeira variável de cada produção:
$$ \begin{aligned} L’ & \to \underbrace{bBZB \alt aXBZB \alt aBBZB \alt bZB \alt bBB \alt aXBB \alt aBBB \alt bB}{MB} \alt b \alt \underbrace{aX}{AX} \alt \underbrace{aB}{AB} \alt \nil \cr X &\to \underbrace{bBZBB \alt aXBZBB \alt aBBZBB \alt bZBB \alt bBBB \alt aXBBB \alt aBBBB \alt bBB \alt bB \alt aXB \alt aBB}{LB}\cr Z &\to \underbrace{bBZ}{BBZ} \alt \underbrace{bB}{BB}\cr B &\to b \cr A &\to a \cr L &\to \underbrace{bBZB \alt aXBZB \alt aBBZB \alt bZB \alt bBB \alt aXBB \alt aBBB \alt bB}_{MB} \alt b \alt aX \alt aB\cr M &\to bBZ \alt aXBZ \alt aBBZ \alt bZ \alt bB \alt aXB \alt aBB \alt b \end{aligned} $$
Sem anotações, a GIC final, $$ \begin{aligned} G^6 =& \del{\set{L’, L, M, A, B, X, Z}, \set{a, b}, \ldots, L’} \cr & \begin{aligned} L’ & \to bBZB \alt aXBZB \alt aBBZB \alt bZB \alt bBB \alt aXBB \alt aBBB \alt bB \alt b \alt aX \alt aB \alt \nil \cr X &\to bBZBB \alt aXBZBB \alt aBBZBB \alt bZBB \alt bBBB \alt aXBBB \alt aBBBB \alt bBB \alt bB \alt aXB \alt aBB\cr Z &\to bBZ \alt bB\cr B &\to b \cr A &\to a \cr L &\to bBZB \alt aXBZB \alt aBBZB \alt bZB \alt bBB \alt aXBB \alt aBBB \alt bB \alt b \alt aX \alt aB\cr M &\to bBZ \alt aXBZ \alt aBBZ \alt bZ \alt bB \alt aXB \alt aBB \alt b \end{aligned} \end{aligned} $$ está na Forma Normal de Greibach e é equivalente à GIC inicial $$ \begin{aligned} G^0 =& \del{\set{L, M, N, O}, \set{a, b, c, d}, \ldots, L} \cr &\begin{aligned} L &\to Mb \alt aLb \alt \nil \cr M &\to Lb \alt MLN \alt \nil \cr N &\to NaN \alt NbO \cr O &\to cO \alt \nil \end{aligned} \end{aligned} $$
Embora $G^6$ tenha muito mais produções do que $G^0$ e ainda por cima aparentemente redundantes (mas não o são) o facto de $G^6$ estar na FNG torna-a mais adequada e eficiente do que $G^0$ em termos de pesquisa. Por exemplo:
- A derivação de uma palavra com $n$ símbolos tem, no máximo, $n$ passos porque cada produção “produz” um terminal.
- O primeiro símbolo “filtra” as possíveis produções aplicáveis.
- A pesquisa de uma palavra não gerada pela GIC, $p \not\in L$, “falha cedo”, no máximo em $\len{p}$ passos.
Ver o exemplo no código deste capítulo.
Processo de Normalização de uma Gramática
Resumindo todos os passos, a normalização de uma GIC consiste em:
- Eliminar a recursividade do símbolo inicial.
- Eliminar as produções vazias exceto, se necessário, do símbolo inicial.
- Eliminar as produções unitárias.
- Eliminar os símbolos inúteis.
- Transformar na Forma Normal de Chomsky.
- Transformar na Forma Normal de Greibach.
Conclusão
O problema da Análise Sintática, que se está a tentar resolver, é uma reformulação do Problema Principal de ALP para as GIC e pergunta “como determinar se $p \in L$” quando $p$ é uma palavra/programa e $L$ é uma linguagem gerada por uma gramática independente de contexto.
Inicialmente tentou-se formalizar as linguagens $L$ usando expressões regulares mas o Pumping Lemma mostrou a necessidade de uma abordagem mais geral — as gramáticas independentes de contexto.
Embora as GIC resolvam a adequação (com as expressões algébricas) e os autómatos de pilha proporcionem um modelo computacional, este não é eficiente.
A Normalização de uma GIC é um processo que começa com uma GIC e que, ao longo de vários passos, produz outras GIC equivalentes, de forma a obter-se uma gramática “adequada” aos algoritmos de pesquisa geral. A Forma Normal de Greibach impõe restrições fortes às produções, que podem ser bem aproveitadas para reduzir a complexidade/ramificação da pesquisa.
Mesmo com a FNG a ajudar na pesquisa, a resposta a “$p \in L$” ainda permite ramificações ao pesquisar a árvore das derivações. Portanto o problema do não determinismo persiste e, com ele, a eficiência fica por resolver.
Os algoritmos deterministas são o próximo assunto e assentam, tanto quanto possível, nas propriedades das gramáticas e das derivações.
Gramáticas LL(k)
 |
|---|
Análise Sintática Descendente Determinista.
Introdução
A Análise Sintática por pesquisa geral não é eficiente, mesmo após a transformação para a FNG porque continua a ser possível encontrarem-se várias produções para expandir um vértice.
Na situação acima o não determinismo resulta as possíveis múltiplas expansões quando se consideram as variáveis em isolamento. Por exemplo, dada a GIC abaixo, o vértice $aS$ tem dois filhos possíveis: $aaS$ e $acA$.
$$ \begin{aligned} S &\to aS \alt cA \cr A &\to bA \alt cB \alt \nil \cr B &\to cB \alt a \alt \nil \end{aligned} $$
Mas uma observação mais cuidadosa da pesquisa, considerando o primeiro símbolo do sufixo que falta derivar mostra uma situação interessante:
| Pesquisa Descendente de $acc$ com Avanço |
|---|
 |
| Em cada vértice podam-se os ramos “incompatíveis”. |
Neste exemplo, olhando para o próximo terminal durante a pesquisa por $acc$ obtém-se uma pesquisa determinista.
Nesta secção exploram-se pesquisas deterministas com o auxílio dos “símbolos seguintes”.
Conteúdo
A apresentação intuitiva acima precisa de uma representação mais formal. Por exemplo, a derivação de $acbb$ pode ser obtida pela seguinte tabela:
$$ \begin{array}{l|r|c|l|r} \text{prefixo} & \text{\alert{avanço}resto} & \text{variável} & \text{produção} & \text{derivação} \cr \nil & \alert{a}cbb & S & S \to aS & S \der aS \cr a & \alert{c}bb & S & S \to cA & \der acA \cr ac & \alert{b}b & A & A \to bA & \der acbA \cr acb & \alert{b} & A & A \to bA & \der acbbA \cr acbb & \alert{\nil} & A & A \to \nil & \der acbb \end{array} $$
Em cada linha:
- Há uma variável ativa, que inicialmente é $S$.
- É escolhida a única produção cujo primeiro símbolo coincide com o símbolo de avanço.
- O avanço é “transferido” para o prefixo processado e a variável ativa é a primeira que ocorre na produção escolhida na linha anterior.
Interessa formalizar esta exploração com vista a definir métodos rigorosos para:
- Determinar se uma GIC é adequada, ou não, a este processo.
- Definir algoritmos eficientes baseados na pesquisa com avanço.
Começando pela definição de gramática “adequada” à pesquisa com avanço:
Gramática LL(1). A GIC $G = \del{V, \Sigma, P, S}$ com terminador $#$ é LL(1) se dadas duas derivações esquerdas $$ \begin{aligned} S \ider u_1 \alert{A} v_1 \der u_1 \alert{x} v_1 \ider u_1 a w_1 \cr S \ider u_2 \alert{A} v_2 \der u_2 \alert{y} v_2 \ider u_2 a w_2 \end{aligned} $$ em que $u_i, w_i \in \cl{\Sigma},\ a\in\Sigma$ e $A \in V$ então $\alert{x = y}$.
N.B. “LL” significa “Left-to-right Leftmost derivation”. Em português: “derivação esquerda da esquerda-para-a-direita”. Note-se que “derivação esquerda” especifica qual é a variável a tratar enquanto que “da esquerda-para-a-direita” indica que a palavra é processada sequencialmente do primeiro símbolo para o último.
N.B. O terminador ocorre exatamente uma vez nas palavras geradas e é sempre o último símbolo. A sua função é garantir que há sempre um símbolo de avanço na palavra analisada. Fica como exercício encontrar um algoritmo que transforma uma GIC qualquer, $A$, noutra, $A’$ com terminador $#$, de forma que $p \in L(A) \iff p\# \in L(A’)$.
Intuitivamente a definição de GIC LL(1) diz que não há duas produções distintas de $A$ que produzem sufixos terminais que começam pelo mesmo terminal. Ou seja, os resultados finais da aplicação de duas produções de $A$ distintas difere logo no primeiro símbolo.
As gramáticas LL(1) têm algumas propriedades interessantes:
Propriedades das Gramáticas LL(1). Seja $G = \del{V, \Sigma, P, S}$ uma GIC:
- Se $G$ é LL(1) então não é ambígua,
- Se alguma variável de $G$ for recursiva à esquerda então $L$ não é LL(1).
A generalização de LL(1) para mais do que um símbolo de avanço é representada por $LL(k)$. Este caso é pouco interessante em termos teóricos porque torna a notação mais críptica sem progredir na resolução da análise sintática.
Note-se que uma gramática na FNG quase que é LL(1). O problema está na possibilidade de várias produções começarem pelo mesmo terminal. Para ajudar a ultrapassar esta situação é preciso “arrumar” as produções que começam pelo mesmo símbolo.
Fatorização à Esquerda. Seja $G=\del{V, \Sigma, P, S}$ uma GIC. Supondo que as produções de $A\in V$ são $$ A \to \alert{p}u_1 \alt \alert{p}u_2 \alt \cdots \alt \alert{p}u_n \alt v_1 \alt v_2 \alt \cdots \alt v_m $$
em que $p, u_i, v_j \in \clpar{V \cup \Sigma}$ então a GIC $G’$ obtida de $G$
- Acrescentando uma nova variável, $Z$.
- Substituindo as produções de $A$ por $A \to \alert{p}Z \alt v_1 \alt v_2 \alt \cdots \alt v_m$.
- Acrescentado as produções $Z \to u_1 \alt u_2 \alt \cdots \alt u_n$.
é equivalente a $G$.
Com a fatorização as várias produções de $A$ que começam pelo mesmo prefixo, $A \to pu_1 \alt pu_2 \alt \cdots \alt pu_n$ ficam agrupadas numa só produção, $A \to pZ$ e a nova variável, $Z$, gera os restantes sufixos.
Por exemplo, recuperando a gramática $G^6$ que ilustrou da construção da FNG:
$$ \begin{array}{c} \text{Forma Normal de Greibach} \cr \begin{aligned} L’ & \to bBZB \alt aXBZB \alt aBBZB \alt bZB \alt bBB \alt aXBB \alt aBBB \alt bB \alt b \alt aX \alt aB \alt \nil \cr &\vdots \end{aligned} \cr \text{Fatorizada (duas aplicações)} \cr \begin{aligned} L’ & \to bZ_1 \alt aZ_2 \alt \nil \cr Z_1 &\to BZB \alt ZB \alt BB \alt B \alt \nil \cr Z_2 &\to XBZB \alt BBZB \alt XBB \alt BBB \alt X \alt B \cr &\vdots \end{aligned} \end{array} $$
A fatorização pode ser aplicada repetidas vezes até que o resultado seja adequado, por exemplo uma GIC LL(1).
Para determinar se uma GIC é LL(1) a partir da definição pode ser confuso. Para ajudar neste problema mas também para definir um algoritmo determinista de análise sintática para gramáticas LL(1) usam-se os primeiros, seguintes e os diretores.
Primeiros. Seguintes. Seja $G = \del{V, \Sigma, P, S}$ uma GIC.
Os primeiros de $u \in \clpar{V \cup \Sigma}$ são os terminais que ocorrem na primeira posição das palavras derivadas de $u$: $$\primeiros\at{u} = \set{a \in \Sigma \st u \ider ax \in \cl{\Sigma}}$$
Os seguintes de $A\in V$ são os terminais que ocorrem imediatamente a seguir a $A$ nalguma derivação de $G$: $$\seguintes\at{A} = \set{a \in \Sigma \st S \ider uAv \land a \in \primeiros\at{v}}$$
Por exemplo, para a GIC $$ \begin{aligned} S &\to aS \alt cA \cr A &\to bA \alt cB \alt \nil \cr B &\to cB \alt a \alt \nil \end{aligned} $$
| O conjunto dos … | … é … |
|---|---|
| primeiros de $ac$ | $\set{a}$ |
| primeiros de $A$ | $\set{b, c}$ |
| seguintes de $S$ | $\empty$ |
A partir da definição não é simples calcular os conjuntos dos primeiros e dos seguintes. Para esse cálculo há dois algoritmos gráficos:
Grafo dos Primeiros. Seja $G = \del{V, \Sigma, P, S}$ uma GIC. O grafo dos primeiros é um grafo em que os vértices são os símbolos de $V \cup \Sigma$ e para cada produção $A \to s_1 s_2 \ldots s_n$:
- Acrescenta-se a aresta $A \longrightarrow s_1$.
- Se $s_1 \in \Lambda$, acrescenta-se a aresta $A \longrightarrow s_2$.
- Assim sucessivamente até se esgotarem os $s_i$ ou $s_i \not\in \Lambda$.
O grafo dos primeiros tem um caminho $A \longrightarrow a \in \Sigma$ se e só se $a \in \primeiros\at{A}$.
Continuando com a GIC anterior, obtém-se
| Exemplo de Grafo dos Primeiros |
|---|
 |
| N.B. Os “cantos” das arestas são arredondados. |
e, portanto, os primeiros de cada variável são:
$$ \begin{array}{c|c} V & \primeiros\at{V} \cr \hline S & \set{a, c} \cr A & \set{b, c} \cr B & \set{a, c} \end{array} $$
ou simplificando a notação: $$ \begin{array}{c|c} & \primeiros \cr \hline S & ac \cr A & bc \cr B & ac \end{array} $$
Este método mostra apenas os primeiros das variáveis. Para as restantes palavras:
Em geral, calculam-se recursivamente os $\primeiros$:
- $\primeiros\at{\nil} = \empty$.
- Para $a\in\Sigma, \primeiros\at{a} = \set{a}$.
- Para $A\in V$ usa-se o grafo dos primeiros.
- Para $uv\in\clpar{V \cup \Sigma}$:
$$ \begin{cases}\primeiros\at{u} \cup \primeiros\at{v} & \text{se}\ u \ider \nil \cr \primeiros\at{u} & \text{caso contrário} \end{cases} $$
Depois dos primeiros (das variáveis) podem calcular-se os seguintes.
Grafo dos Seguintes. Seja $G = \del{V, \Sigma, P, S}$ uma GIC. O grafo dos seguintes é um grafo em que os vértices são os símbolos de $V \cup \Sigma$ e para cada produção $A \to uBv$ com $B\in V, u,v \in \clpar{V \cup \Sigma}$:
- Acrescenta-se uma aresta $B \longrightarrow a$ para cada $a \in \primeiros\at{v}$.
- Se $v \ider \nil$, acrescenta-se a aresta $B \longrightarrow A$.
O grafo dos seguintes tem um caminho $A \longrightarrow a \in \Sigma$ se e só se $a \in \seguintes\at{A}$.
Continuando com o mesmo exemplo:
| Exemplo de Grafo dos Seguintes |
|---|
 |
donde resulta $$ \begin{array}{c|c} & \seguintes \cr \hline S & \empty \cr A & \empty \cr B & \empty \end{array} $$
O próximo passo consiste em determinar os primeiros símbolos que cada produção gera.
Diretores. Seja $G=\del{V, \Sigma, P, S}$ uma GIC e $A \to p \in P$. O conjunto dos diretores de $A \to p$ é: $$\diretores\at{A \to p} = \begin{cases} \primeiros\at{p} \cup \seguintes\at{A} & \text{se}\ p \ider \nil\cr \primeiros\at{p} & \text{caso contrário} \end{cases} $$
Depois de calculados os primeiros e os seguintes, os diretores são facilmente encontrados: $$ \begin{array}{l|cr} & \diretores \cr \hline S \to aS & a \cr S \to cA & c \cr S \to \nil & \empty & \checkmark\cr \hline A \to bA & b \cr A \to cB & c\cr A \to \nil & \empty & \checkmark\cr \hline B \to cB & c \cr B \to a & a\cr B \to \nil & \empty & \checkmark \end{array} $$
Os diretores permitem facilmente verificar se uma GIC é LL(1):
Teorema dos Diretores. Seja $G = \del{V, \Sigma, P, S}$ uma GIC. Se, para qualquer variável $A \in V$ quaisquer duas produções de $A$ tiverem os respetivos diretores distintos, isto é, se $$\diretores\at{A \to u} \cap \diretores\at{A \to v} = \empty$$ para quaisquer duas produções de $A$, então $G$ é LL(1)
Exemplos de Aplicação do Teorema dos Diretores
A GIC definida por $S \to aSa \alt bSb \alt \nil$ não é LL(1):
$$ \begin{array}{c|c|c} & \primeiros & \seguintes \cr \hline S & ab & ab \end{array} $$ e $$ \begin{array}{l|cr} & \diretores \cr \hline S \to aSa & a \cr S \to bSb & b \cr S \to \nil & ab & \text{nok} \end{array} $$ Como $$\diretores\at{S \to \nil} \cap \diretores\at{S \to aSa} = \set{a,b} \cap \set{a} = \set{a} \not= \empty$$ conclui-se que esta gramática não é LL(1).
Um caso mais interessante é a seguinte variante das expressões algébricas, que ilustra a aplicação de algumas transformações:
$$ \begin{aligned} S &\to E\#\ \cr \alert{E} &\to \alert{E} + T \alt T & \text{recursão direta à esquerda} \cr T &\to (E) \alt a \cr \hline S & \to E\# \cr E &\to \alert{TZ} \alt \alert{T} &\text{prefixos comuns} \cr Z &\to \alert{+T}Z \alt \alert{+T} &\text{prefixos comuns} \cr T &\to (E) \alt a \cr \hline S &\to E\# \cr E &\to TF \cr F &\to \alert{Z \alt \nil} &\text{repetida}\cr Z &\to +TW \cr W &\to \alert{Z \alt \nil} &\text{repetida}\cr T &\to (E) \alt a \cr \hline \hline S &\to E\# \cr E &\to TX \cr Z &\to +TX \cr X &\to Z \alt \nil \cr T &\to (E) \alt a \end{aligned} $$
Para verificar se esta última gramática é LL(1), passo a passo:
Geradores de Vazio
$$ \Lambda = \set{X}. $$
Primeiros
| Grafo dos Primeiros |
|---|
 |
Seguindo as arestas:
$$ \begin{array}{l|l} &\primeiros \cr \hline S & (\ a \cr E & (\ a \cr Z & + \cr X & + \cr T & (\ a \end{array} $$
Seguintes
| Grafo dos Seguintes |
|---|
 |
Seguindo as arestas:
$$ \begin{array}{l|l} &\seguintes \cr \hline S \cr E & \#\ ) \cr Z & \#\ ) \cr X & \#\ ) \cr T & \#\ )\ + \end{array} $$
Diretores
$$ \begin{array}{rl|lr} &&\diretores \cr \hline S &\to E\# & (\ a\cr \hline E &\to TX & (\ a \cr \hline Z &\to +TX & + \cr \hline X &\to Z & +\cr X &\to \nil & \#\ ) && \checkmark\cr \hline T &\to (E) & (\cr T &\to a & a && \checkmark \end{array} $$
Analisador Sintático
Com os diretores de cada produção calculados, se a gramática for LL(1), é simples implementar manualmente um Analisador Sintático para essa gramática:
def S():
if seguinte in "(a":
E()
consome("#")
else:
erro()
def E():
if seguinte in "(a":
T()
X()
else:
erro()
def Z():
if seguinte in "+":
consome("+")
T()
X()
else:
erro()
def X():
if seguinte in "+":
Z()
elif seguinte in "#)":
return
else:
erro()
def T():
if seguinte in "(":
consome("(")
E()
consome("(")
elif seguinte in "a":
consome("a")
else:
return erro()
def consome(terminal):
if terminal == seguinte:
# AVANÇA
seguinte = ...
else:
erro()
def erro():
# Para o processamento
...
Um exemplo deste programa a correr, para analisar a palavra a+a#, é:
| “pilha” | seguinte | resto |
|---|---|---|
S() | a | +a# |
E(); consome(#) | a | +a# |
T(); X(); consome(#) | a | +a# |
consome(a); X(); consome(#) | a | +a# |
X(); consome(#) | + | a# |
Z(); consome(#) | + | a# |
consome(+); T(); X(); consome(#) | + | a# |
T(); X(); consome(#) | a | # |
consome(a); X(); consome(#) | a | # |
X(); consome(#) | # | (vazio) |
consome(#) | # | (vazio) |
| (vazio) | (nenhum) | (vazio) |
O resultado deste analisador sintático é “verdade” ou “falso” conforme a palavra dada é, ou não, gerada pela gramática. Este é o resultado esperado mas insatisfatório pois nada diz sobre a derivação, isto é a estrutura, da palavra.
Por exemplo, dada a palavra a+a# é desejável saber, além de que $G \ider a+a\#$, que a sua derivação esquerda é
$$
S \nder{S \to E\#} E\# \nder{E\to E + T} E + T\# \nder{E\to T} T + T\# \nder{T \to a} a + T\# \nder{T \to a} a + a\#
$$
na gramática inicial.
Conclusão
Este último exemplo mostra que a Análise Sintática está quase resolvida:
As GIC LL(1) são adequadas para representar as linguagens de programação. Além disso, é possível definir algoritmos eficientes para determinar computacionalmente se uma palavra é, ou não, gerada por essa gramática.
No entanto… ainda há por onde melhorar esta situação:
- A transformação de uma GIC noutra que seja LL(1) é um passo Ad hoc, que depende de muitas escolhas específicas.
- Nessa transformação perde-se a ligação à gramática inicial. Em concreto, olhando para a computação de
a+a#não se percebe como a palavra é gerada pelas produções da gramática inicial. - Este processo implica a implementação “manual” das “produções” (human in the middle) mas seria muito melhor que fosse totalmente automático. Isto é, pretende-se definir um programa “geral”
Superque aceita como entrada uma gramáticaGe devolve um certo programaPque, por sua vez, aceita como entrada uma palavrape calcula se esta é, ou não, gerada porG:P = Super(G).P(p)é equivalente a “pé gerada porG”.
Gramáticas LR(k)
Análise Sintática Ascendente Determinista.
Introdução
As gramáticas LL(1) resolvem o problema da Análise Sintática no sentido em que proporcionam:
- Uma representação adequada para definir linguagens de programação.
- Um método computacional e eficiente para determinar se uma palavra é gerada por uma gramática.
No entanto a construção do analisador sintático LL(1) a partir de uma GIC arbitrária implica alguns passos manuais (human in the middle) que devem ser evitados.
O objetivo para esta secção é resolver esses problemas:
Obter um programa que tem como entrada uma GIC e que produz um segundo programa que tem como entrada uma palavra e que determina se essa palavra pertence, ou não, à linguagem dada ao primeiro programa. Isto é, definir um programa
Supertal que:
- Se
Gfor uma GIC,P = Super(G).- Seja
puma palavra.P(p)é “verdade” ou “falso” conformeGgera, ou não,p.- Tanto
SuperePsão eficientes.
Conteúdo
Para atingir esse objetivo:
- São definidas as gramáticas LR(k), Left-to-right Rightmost derivation in reverse, em português “derivação direita da esquerda-para-a-direita em reverso”, onde “em reverso” significa que os passos da derivação são descobertos do último para o primeiro, isto é, como numa pesquisa ascendente.
- Dada uma gramática LR(n) é construído um analisador sintático como autómato de pilha determinista.
Estes analisadores sintáticos são eficientes no sentido em que detetam erros sintáticos assim que possível (isto é, quando a gramática não gera a palavra) mas (como se vai ver) o processo para os construir é muito trabalhoso quando feito à mão.
O “k” em LR(k) refere-se ao número de símbolos de avanço necessários para escolher deterministicamente as operações do AP. Para as gramáticas LR(0) não é preciso qualquer avanço, para as LR(1) é necessário um símbolo de avanço, etc.
Gramáticas LR(0)
Tal como antes para as gramáticas LL, o interesse aqui está nas gramáticas LR(1) porém o caso LR(0) é importante como introdução para o processo de construção do analisador sintático.
Contextos LR(0)
Problema. Quando é que uma produção pode ser aplicada numa derivação “válida”?
Isto é, será possível determinar quando a aplicação de uma produção numa derivação contribui para uma palavra gerada pela gramática das outras aplicações, em que o resultado não é gerado pela gramática?
No caso das derivações direitas
Contexto-LR(0). Prefixo Viável. Seja $G=\del{V, \Sigma, P, S}$ uma GIC com terminador $\#$ e em que $S$ não é recursivo.
A palavra $\alert{up} \in \clpar{V \cup \Sigma}$ é um Contexto-LR(0) da produção $A \to p$ se existir uma derivação direita $$S \iderR uAv \derR \alert{up}v, v \in \cl{\Sigma}.$$
- Isto é, há uma redução $upv \stackrel{\ast}{\Leftarrow}_R S$ que começa por $A \to p$.
Um prefixo viável é um prefixo de um contexto-LR(0).
Dada uma produção, o conjunto dos seus contextos-LR(0) é uma linguagem regular.
N.B. Na definição acima é importante ter presente que se tratam de derivações direitas. Portanto, quando $A\to p$ é aplicada em $uAv$:
- O sufixo $v$ é formado só por terminais.
- O prefixo $u$ é o “contexto” para a aplicação da regra $A\to p$.
Intuitivamente pretende-se que os Contextos-LR(0) tenham informação suficiente para determinar que produção aplicar em cada passo de uma derivação. Isto é, se os Contextos-LR(0) forem disjuntos tem-se um método determinista para fazer derivações direitas.
Por exemplo, dada a GIC $$ \begin{aligned} S &\to aA \alt aB \cr A &\to aAb \alt b \cr B &\to bBa \alt b \end{aligned} $$
As derivações direitas têm uma das seguintes formas
$$ \begin{aligned} S &\nderR{S \to aA} &aA &\nderR{A\to aAb} &\ldots &\nderR{A\to aAb} &aa^n A b^n &\nderR{A \to b} &aa^n bb^n \cr S &\nderR{S \to aB} &aB &\nderR{B\to aBa} &\ldots &\nderR{B\to bBa} &ab^n B a^n &\nderR{B \to b} &ab^n ba^n \end{aligned} $$
pelo que os Contextos-LR(0) das produções são:
$$ \begin{array}{lr} \text{produção} & \text{Contexto-LR(0)} \cr \hline S \to aA & \set{aA} \cr S \to aB & \set{aB} \cr A \to aAb & \set{a^naAb \st n > 0} \cr A \to b & \set{aa^n b \st n \geq 0} \cr B \to bBa & \set{ab^nbBa \st n \geq 0} \cr B \to b & \set{ab^nb \st n \geq 0} \end{array} $$
Neste caso, $ab$ é um contexto-LR(0) tanto de $A \to b$ como de $B \to b$ (com $n = 0$ em ambos os casos).
O que é que isto significa? Quando se procura descobrir como $ab$ poderá ter sido derivada à direita, há duas possibilidades:
- Ou $S \nderR{S \to aA} aA \nderR{A \to b} ab$.
- Ou $S \nderR{S \to aB} aB \nderR{B \to b} ab$.
Isto é, em $ab$ não “há informação suficiente” para saber qual foi a última produção aplicada, $A \to b$ ou $B \to b$.
Considerando agora a GIC
$$ \begin{aligned} S &\to X\# \cr X &\to XY \alt \nil \cr Y &\to aYa \alt b \end{aligned} $$ os contextos-LR(0) são: $$ \begin{array}{lr} S \to X\# & X\# \cr X \to XY & XY \cr X \to \nil & \nil \cr Y \to aYa & X\cl{a} aYa\cr Y \to b & X\cl{a}b \end{array} $$
Os contextos-LR(0) podem ser descobertos explorando a árvore das derivações direitas:
| Árvore das Derivações Direitas |
|---|
 |
| Os contextos-LR(0) estão sublinhados. |
Agora, para encontrar uma derivação de $aabaa\#$:
- O maior prefixo de $aabaa\#$ que é um contexto-LR(0) é $\nil$, de $X \to \nil$.
- Portanto, a produção aplicada foi $X \to \nil$, à palavra $Xaabaa\#$.
- O maior prefixo de $Xaabaa\#$ que é um contexto-LR(0) é $Xaab$, de $Y \to b$.
- Portanto, foi aplicada $Y \to b$ a $XaaYaa\#$.
- O maior prefixo de $XaaYaa\#$ que é um contexto-LR(0) é $XaaYa$, de $Y \to aYa$.
- Portanto, foi aplicada $Y \to aYa$ a $XaYa\#$.
- O maior prefixo de $XaYa\#$ que é um contexto-LR(0) é $XaYa$, de $Y \to aYa$.
- Portanto, foi aplicada $Y \to aYa$ a $XY\#$.
- O maior prefixo de $XY\#$ que é um contexto-LR(0) é $XY$, de $X \to XY$.
- Portanto, foi aplicada $X \to XY$ a $X\#$.
- O maior prefixo de $X\#$ que é um contexto-LR(0) é $X\#$, de $S \to X\#$.
- Portanto, foi aplicada $S \to X\#$ e a derivação está encontrada:
$$ S \nderR{S \to X\#} X\# \nderR{X \to XY} XY \# \nderR{Y \to aYa} XaYa\# \nderR{Y \to aYa} XaaYaa\# \nderR{Y \to b} Xaabaa\# \nderR{X \to \nil} aabaa\# $$
Note-se que:
- Foi encontrada uma derivação direita (rightmost derivation).
- A “pilha” é lida da esquerda-para-a-direita (left-to-right).
- O processo encontra a derivação em reverso (in reverse).
A derivação anterior pode ser organizada numa tabela com quatro tipos de ações:
- Reduzir $A\to w$ quando a pilha tem um Contexto-LR(0) de $A\to w$.
- Transferir o primeiro símbolo da palavra para a pilha, quando a pilha tem um prefixo viável que não é um Contexto-LR(0).
- Aceitar quando a pilha é $S$ e a palavra $\nil$.
- Rejeitar quando a pilha não é um prefixo viável.
O resultado é: $$ \begin{array}{ll|cl} \text{pilha} & \text{palavra} & \text{Contexto} & \text{ação} \cr \hline \nil & aabaa\# & X \to \nil & R \cr X & aabaa\# & \text{viável} & T \cr Xa & abaa\# & \text{viável} & T \cr Xaa & baa\# & \text{viável} & T \cr Xaab & aa\# & Y \to b & R \cr XaaY & aa\# & \text{viável} & T \cr XaaYa & a\# & Y \to aYa & R \cr XaY & a\# & \text{viável} & T \cr XaYa & \# & T \to aYa & R \cr XY & \# & X \to XY & R \cr X & \# & \text{viável} & T\cr X\# & \nil & S \to X\# & R \cr S & \nil && \text{aceitar} \end{array} $$
A derivação de $aabaa\#$ pode ser recuperada da coluna “ação”, lida em reverso.
Para procurar uma derivação de $abb\#$, que não é gerada pela gramática: $$ \begin{array}{ll|cl} \text{pilha} & \text{palavra} & \text{Contexto} & \text{ação} \cr \hline \nil & abb\# & X \to \nil & R \cr X & abb\# & \text{viável} & T \cr Xa & bb\# & \text{viável} & T \cr Xab & b\# & Y \to b & R \cr XaY & b\# & \text{viável} & T \cr XaYb & \# & \text{inviável} & \text{rejeitar} \end{array} $$
Itens LR(0)
Os exemplos acima ilustram a utilidade dos contextos-LR(0) para a análise sintática. Embora não sejam facilmente encontrados a partir da definição, o conjunto dos Contextos-LR(0) de uma produção é uma linguagem regular que pode ser definida por um certo autómato finito determinista.
Para definir esse AFD é preciso começar pelos seus estados:
Item LR(0). Seja $G=\del{V, \Sigma, P, V}$ uma GIC.
- Os itens LR(0) de $G$ são as “produções” que se obtêm de $P$ acrescentado um $\cdot$ em todas as posições possíveis:
- Se $A \to \nil \in P$ então $A \to \cdot$ é um item LR(0) de $G$.
- Se $A \to uv \in P$ então $A \to u \cdot v$ é um item LR(0) de $G$.
- Um item completo é um item em que o $\cdot$ está o mais à direita possível.
- Um item $A \to u \cdot v$ é válido para o prefixo viável $xu$ se $xuv$ é um contexto LR(0); Isto é, se $A \to uv$ é candidato a reduzir.
Usando a gramática do exemplo anterior, os seus itens LR(0) são $$ \begin{aligned} S &\to \cdot X \# & S &\to X \cdot \# & \alert{S} &\alert{\to X\# \cdot} \cr X &\to \cdot XY & X &\to X \cdot Y & \alert{X} &\alert{\to XY \cdot} \cr \alert{X} &\alert{\to \cdot} \cr Y &\to \cdot aYa & Y &\to a\cdot Ya &Y &\to aY\cdot a &\alert{Y} &\alert{\to aYa \cdot }\cr Y &\to \cdot b & \alert{Y} &\alert{\to b \cdot} \end{aligned} $$ com os itens completos assinalados assim: $\alert{A \to p\cdot}$.
Fecho. Seja $I$ um conjunto de itens. O fecho de $I$, denotado $\fecho\at{I}$ define-se recursivamente por:
- base $I \subseteq \fecho\at{I}$.
- passo Se $A \to u\cdot Bv \in \fecho\at{I}$ com $B \in V$ então, para cada produção $B \to p \in P$, também $B \to \cdot p \in \fecho\at{I}$.
Por exemplo, usando a gramática anterior,
$$\fecho\at{X\to X\cdot Y} = \set{X \to X \cdot Y, Y \to \cdot aYa, Y \to \cdot b}$$
Autómato Finito dos Itens LR(0) Válidos
Os fechos dos itens são usado para construir um autómato finito que determina a ação nas tabelas acima.
Autómato dos Itens Válidos (AIV). Seja $G = \del{V, \Sigma, P, S}$ uma GIC. O autómato dos itens válidos, que reconhece os prefixos viáveis de $G$ é o AFD $A = \del{Q, V \cup \Sigma, \delta, q_I, Q \setminus \set{\empty}}$ em que:
- estado inicial $q_I = \fecho\at{\set{S\to \cdot p \st S \to p \in P}}$.
- transição Para cada $q \in Q$ e $x \in V \cup \Sigma$
$$\delta\at{q, x} = \fecho\at{\set{A \to u\alert{x\cdot} v \st A \to u\alert{\cdot x} v \in q}}$$
Continuando com a gramática anterior, o seu autómato dos itens válidos tem os seguintes estados e transição:
$$ \begin{array}{c|cl||cc} \text{estado} & \exists\text{completo}? & \text{itens} & \text{símbolo} & \text{para} \cr \hline \q{0} & \checkmark & S \to \cdot X \#, X \to \cdot XY, X \to \cdot \cr &&& X & \q{1} \cr \hline \q{1} && S \to X \cdot \#, X \to X \cdot Y, Y \to \cdot aYa, Y \to \cdot b \cr &&& \# & \q{2} \cr &&& Y & \q{3} \cr &&& a & \q{4} \cr &&& b & \q{5} \cr \hline \q{2} & \checkmark & S \to X \#\cdot \cr \hline \q{3} & \checkmark & X \to XY \cdot \cr \hline \q{4} && Y \to a \cdot Y a, Y \to \cdot aYa, Y \to \cdot b \cr &&& Y & \q{6} \cr &&& a & \q{4} \cr &&& b & \q{5} \cr \hline \q{5} &\checkmark & Y \to b \cdot \cr \hline \q{6} && Y \to a Y \cdot a\cr &&& a & \q{7} \cr \q{7} & \checkmark& Y \to a Y a \cdot \cr \end{array} $$
Note-se que há mais um estado, $\empty$, que não se representa e que recebe todas as transições que não estão especificadas.
Este AFD pode ser representado numa tabela mais convencional (todas as transições não assinaladas vão para $\empty$):
$$ \begin{array}{r|cccccc} q & S & X & Y & a & b & \# \cr \hline if\q{0} && \q{1} \cr f\q{1} &&& \q{3} & \q{4} & \q{5} & \q{2} \cr f\q{2} \cr f\q{3} \cr f\q{4} &&& \q{6} & \q{4} & \q{5} \cr f\q{5} \cr f\q{6} &&&& \q{7} \cr f\q{7} \cr \empty \end{array} $$
Porém, pode ser mais simples calcular graficamente os estados e a transição do autómato dos itens válidos.
| Diagrama do Autómato dos Itens Válidos |
|---|
 |
| Em cada estado os itens completos são assinalados com $\star$. O estado $\empty$ não está representado. |
Neste diagrama cada estado tem dois ou três “andares”. De cima para baixo:
- O “nome” do estado, um inteiro $\q{0}, \q{1}, \ldots$
- A “raiz” dos itens, que resultam da transição.
- Restantes itens, para se obter o fecho da “raiz”.
Analisador Sintático LR(0)
O Autómato dos itens válidos serve para determinar a ação na derivação. Em cada passo o AIV processa a pilha e a ação é:
- Aceitar se a pilha tem apenas $S$.
- Reduzir se terminar num estado com um item completo. Nesse caso a redução é da produção do item completo.
- Transferir o próximo símbolo da palavra se terminar num estado sem itens completos.
- Rejeitar se não puder processar a palavra (isto é, vai parar a $\empty$).
Recuperando o exemplo anterior, o processamento de $aabaa\#$ é:
$$ \begin{array}{ll|cl} \text{pilha} & \text{palavra} &\text{estado AIV} & \text{ação} \cr \hline \nil & aabaa\# & \q{0} & R: X \to \nil \cr X & aabaa\# & \q{1} & T \cr Xa & abaa\# & \q{4} & T \cr Xaa & baa\# & \q{4} & T \cr Xaab & aa\# & \q{5} & R: Y \to b \cr XaaY & aa\# & \q{6} & T \cr XaaYa & a\# & \q{7} & R: Y \to aYa \cr XaY & a\# & \q{6} & T \cr XaYa & \# & \q{7} & R: T \to aYa \cr XY & \# & \q{3} & R: X \to XY \cr X & \# & \q{1} & T\cr X\# & \nil & \q{2} & R: S \to X\# \cr S & \nil & & \text{aceitar} \end{array} $$
enquanto que para $abb\#$, que não é gerada pela gramática: $$ \begin{array}{ll|cl} \text{pilha} & \text{palavra} & \text{estado AIV} & \text{ação} \cr \hline \nil & abb\# & \q{0} & R: X \to \nil \cr X & abb\# & \q{1} & T \cr Xa & bb\# & \q{4} & T \cr Xab & b\# & \q{5} & R: Y \to b \cr XaY & b\# & \q{6} & T \cr XaYb & \# & \empty & \text{rejeitar} \end{array} $$
Tabela de Análise Sintática LR(0)
A tabela de análise sintática (TAS) estende a transição do AIV com as ações associadas aos respetivos estados. Tem uma linha para cada estado e uma coluna para cada símbolo de $V \cup \Sigma$. Além disso tem também uma coluna, $\text{ação}$, que indica que ação corresponde a um prefixo que termine nesse estado.
Para a gramática que tem vindo a servir de exemplo, a TAS é:
$$ \begin{array}{r|ccc|ccc||l} q & S & X & Y & a & b & \# & \text{ação} \cr \hline \q{0} && \q{1} &&&&& R: X \to \nil \cr \q{1} &&& \q{3} & \q{4} & \q{5} & \q{2} & T \cr \q{2} &&&&&&& A \cr \q{3} &&&&&&& R: X \to XY \cr \q{4} &&& \q{6} & \q{4} & \q{5} && T \cr \q{5} &&&&&&& R: Y \to b\cr \q{6} &&&& \q{7} &&& T\cr \q{7} &&&&&&& R: Y \to aYa\cr \end{array} $$
Nesta tabela:
- O estado $\empty$, a que corresponde a ação “rejeitar”, não é representado e portanto todos os estados mostrados na TAS são finais.
- As transições não representadas levam ao estado $\empty$.
- Por convenção, o estado $\q{0}$ é o inicial.
- Nos estados com itens completos do símbolo inicial da GIC (no exemplo acima, o estado $\q{2}$) a ação é “aceitar”, $A$, em vez de ser “reduzir”, $R$.
Dado que a coluna $\text{ação}$ determina se no analisador sintático é feita uma transferência ou uma redução (e nesse caso, de que produção), se essa informação for ambígua não é possível fazer análise sintática determinista LR(0).
Portanto é necessário que cada estado defina exatamente uma ação.
Como as reduções são feitas em estados com itens completos (por exemplo, os estados $\q{0}, \q{2}, \q{3}, \q{5}, \q{7}$ acima) e as transferência são feitas em estados de que sai alguma “aresta com um terminal” (os estados $\q{1}, \q{4}, \q{6}$ acima), as ambiguidades (conflitos) possíveis são:
- Conflito Redução/Redução LR(0): Se num estado estiverem dois itens completos então esse estado define duas reduções possíveis.
- Conflito Redução/Transferência LR(0): Se num estado com um item completo sair uma aresta “com um terminal” então esse estado define uma redução e uma transferência.
Estas condições permitem caraterizar as gramáticas LR(0):
Teorema das Gramáticas LR(0). Uma GIC é LR(0) se e só se o seu AIV não tem conflitos redução/redução LR(0) nem redução/transferência LR(0).
Autómato de Pilha LR(0)
Pretende-se não só fazer análise sintática determinista mas também que esta seja livre de passos manuais (human in the middle). O AIV proporciona dois passos desse processo:
- Determina se a GIC dada é LR(0).
- Define a ação em cada passo do analisador sintático.
Falta definir formalmente o processamento do próprio analisador sintático, o que será feito com um autómato de pilha.
Autómato de Pilha Reconhecedor LR(0). Seja $G=(V, \Sigma, P, S)$ uma GIC LR(0) e $A = (Q, V\cup \Sigma, \delta_A, \q{0}, Q \setminus \set{\empty})$ o seu AIV. O Autómato de Pilha Reconhecedor (APR) de $G$, que reconhece a linguagem gerada por $G$, é $$R = \del{\set{p_I, p}, \Sigma, V \cup \Sigma \cup Q \setminus \set{\empty}, \delta, p_I, \set{p}}$$ em que a transição, $\delta$, é definida pelos seguintes elementos:
- iniciar: $\alert{\del{p, \q{0}} \in \delta\at{p_I, \nil, \nil}}$.
- transferir: $\alert{\del{p, q’ a q} \in \delta\at{p, a, q}}$ se $q’ = \delta_A\at{q, a}$ com $a \in \Sigma$.
- reduzir: Para cada estado $q_n \in Q$ com um item completo $A \to a_1 a_2 \cdots a_n\cdot$ com $A \not= S$ e $q’ = \delta_A\at{q_0, A}$, $\alert{\del{p, q’ A q_0} \in \delta\at{p, \nil, q_n a_n \cdots q_2 a_2 q_1 a_1 q_0}}$ quando no AIV existe a computação $$q_0 \trf{a_1} q_1 \trf{a_2} q_2 \cdots \trf{a_n} q_n.$$
- aceitar: Para cada estado $q_n \in Q$ com um item completo $S \to a_1 a_2 \cdots a_n\cdot$ do símbolo inicial da GIC, $\alert{\del{p, \nil} \in \delta\at{p, \nil, q_n a_n \cdots q_2 a_2 q_1 a_1 \q{0}}}$ quando no AIV existe a computação $$\q{0} \trf{a_1} q_1 \trf{a_2} \cdots \trf{a_n} q_n.$$
Intuitivamente a pilha do APR intercala estados do AIC com símbolos de $V \cup \Sigma$ de forma a descrever “fragmentos de computação do AIV”. Por exemplo, a computação de $abb\#$ é $$ \begin{array}{ll|cl||rrr} \text{pilha} & \text{palavra} & \text{estado AIV} & \text{ação} & \text{pilha APR} & \text{topo: de} & \text{topo: para} \cr \hline \nil & abb\# & \q{0} & R: X \to \nil & \q{0} & \q{0} & \q{1} X \q{0}\cr X & abb\# & \q{1} & T & \q{1}X\q{0} & \q{1} & \q{4} a \q{1} \cr Xa & bb\# & \q{4} & T & \q{4}a\q{1}X\q{0} & \q{4} & \q{5} b \q{4} \cr Xab & b\# & \q{5} & R: Y \to b & \q{5}b\q{4}a\q{1}X\q{0} & \q{5}b\q{4} & \q{6}Y\q{4}\cr XaY & b\# & \q{6} & T & \q{6}Y\q{4}a\q{1}X\q{0} & \q{6} & \alert{\empty} b \q{6} \cr XaYb & \# & \empty & \text{rejeitar} & \alert{\empty} b\q{6}Y\q{4}a\q{1}X\q{0} \end{array} $$ enquanto que de $aabaa\#$ é: $$ \begin{array}{ll|cl||r} \text{pilha} & \text{palavra} & \text{estado AIV} & \text{ação} & \text{pilha APR} \cr \hline \nil & aabaa\# & \q{0} & R: X \to \nil & \q{0} \cr X & aabaa\# & \q{1} & T & \q{1}X\q{0} \cr Xa & abaa\# & \q{4} & T & \q{4}a\q{1}X\q{0} \cr Xaa & baa\# & \q{4} & T & \q{4}a\q{4}a\q{1}X\q{0} \cr Xaab & aa\# & \q{5} & R: Y \to b & \q{5}b\q{4}a\q{4}a\q{1}X\q{0} \cr XaaY & aa\# & \q{6} & T & \q{6}Y\q{4}a\q{4}a\q{1}X\q{0} \cr XaaYa & a\# & \q{7} & R: Y \to aYa & \q{7}a\q{6}Y\q{4}a\q{4}a\q{1}X\q{0} \cr XaY & a\# & \q{6} & T & \q{6}Y\q{4}a\q{1}X\q{0} \cr XaYa & \# & \q{7} & R: T \to aYa & \q{7}a\q{6}Y\q{4}a\q{1}X\q{0} \cr XY & \# & \q{3} & R: X \to XY & \q{3}Y\q{1}X\q{0} \cr X & \# & \q{1} & T & \q{1}X\q{0} \cr X\# & \nil & \q{2} & R: S \to X\# & \q{2} \# \q{1}X\q{0} \cr S & \nil & & \text{aceitar} & \nil \end{array} $$
Estes exemplos ilustram como o topo da pilha determina a transição do APR: O primeiro símbolo identifica o estado do AIV e este define ou uma transferência ou uma redução (incluindo o caso particular da aceitação).
- No caso de reduzir (ou aceitar) são considerados mais símbolos da pilha, de forma a “capturar” todo o lado direito da produção, que é substituído pela respetiva variável.
- No caso da operação ser uma transferência o terminal da palavra é comparado com a parte correspondente na pilha e, se coincidirem, ambos são “consumidos”.
Neste processo é mantido o registo dos estados do AIV percorridos pelas respetivas computações.
Alternativamente as transições do APR podem ser definidas pela seguinte tabela:
$$ \begin{array}{l||l|lcr} \text{Operação} & \text{Condição} & \text{De} & \text{Aresta} & \text{Para} \cr \hline \text{Iniciar}\cr & & p_I & \nil, \nil/\q{0} & p \cr\cr \hline \text{Transferir}\cr &q’ = \delta_A\at{q, a} & p & a, q / q’ a q & p \cr\cr \hline \text{Reduzir}\cr &A \to a_1 \cdots a_n\cdot\star \in q & p & \nil, \alpha / \beta & p \cr & A \not= S \cr \cr & q_0 \trf{a_1} \cdots \trf{a_n} q_n, q_n = q \cr & \alpha = q_n a_n \cdots a_1 q_0 \cr \cr & q_0 \trf{A} q’ \cr & \beta = q’ A q_0 \cr\cr \hline \text{Aceitar}\cr &S \to a_1 \cdots a_n\cdot\star \in q & p & \nil, \alpha / \nil & p \cr \cr & \q{0} \trf{a_1} \cdots \trf{a_n} q_n, q_n =q \cr & \alpha = q_n a_n \cdots a_1 \q{0} \end{array} $$
Por exemplo para a GIC anterior, com a TAS (calculada acima, repetida aqui)
$$ \begin{array}{r|ccc|ccc||l} q & S & X & Y & a & b & \# & \text{ação} \cr \hline \q{0} && \q{1} &&&&& R: X \to \nil \cr \q{1} &&& \q{3} & \q{4} & \q{5} & \q{2} & T \cr \q{2} &&&&&&& A \cr \q{3} &&&&&&& R: X \to XY \cr \q{4} &&& \q{6} & \q{4} & \q{5} && T \cr \q{5} &&&&&&& R: Y \to b\cr \q{6} &&&& \q{7} &&& T\cr \q{7} &&&&&&& R: Y \to aYa\cr \end{array} $$ as transições do APR são:
-
iniciar $\nil,\nil/\q{0}$ é a única transição $p_I \to p$.
-
transferir Estas transições são $p \tr p$:
$$ \begin{array}{l|r} \text{AIV: Computação} & \text{APR: Transição} \cr \hline \q{1} \trf{a} \q{4} & a, \q{1} / \q{4}a\q{1} \cr \q{1} \trf{b} \q{5} & b, \q{1} / \q{5}b\q{1} \cr \q{1} \trf{\#} \q{2}& \#, \q{1} / \q{2}\#\q{1} \cr \hline \q{4} \trf{a} \q{4} & a, \q{4} / \q{4}a\q{4} \cr \q{4} \trf{b} \q{5} & b, \q{4} / \q{5}b\q{4} \cr \hline \q{6} \trf{a} \q{7} & a, \q{6} / \q{7}a\q{6} \cr \end{array} $$
-
reduzir Estas transições são $p \tr p$:
$$ \begin{array}{lll|r} \text{AIV: Estado} & \text{AIV: Item completo de}\ A\not= S & \text{AIV: Computação} & \text{APR: Transição} \cr \hline \q{0} & X \to \nil \cdot & \q{0} & \nil, \q{0}/\q{1}X\q{0} \cr \hline \q{3} & X \to XY \cdot & \q{0} \trf{X} \q{1} \trf{Y} \q{3} & \nil,\q{3}Y\q{1}X\q{0}/ \q{1} X \q{0} \cr \hline \q{5} & Y \to b \cdot & \q{1} \trf{b} \q{5} & \nil, \q{5}b\q{1}/\q{3}Y\q{1} \cr && \q{4} \trf{b} \q{5} & \nil, \q{5}b\q{4}/\q{6}Y\q{4} \cr \hline \q{7} & Y \to aYa \cdot & \q{1} \trf{a} \q{4} \trf{Y} \q{6} \trf{a} \q{7} & \nil, \q{7}a\q{6}Y\q{4}a\q{1}/\q{3}Y\q{1} \cr && \q{4} \trf{a} \q{4} \trf{Y} \q{6} \trf{a} \q{7} & \nil, \q{7}a\q{6}Y\q{4}a\q{4}/\q{6}Y\q{4} \cr \end{array} $$
-
aceitar Estas transições são $p \tr p$:
$$ \begin{array}{lll|r} \text{AIV: Estado} & \text{AIV: Item completo de}\ S & \text{AIV: Computação} & \text{APR: Transição} \cr \hline \q{2} & S \to X\# \cdot & \q{0} \trf{X} \q{1} \trf{\#} \q{2} & \nil, \q{2}\# \q{1} X \q{0}/\nil \end{array} $$
O diagrama do APR é:
| Diagrama do APR |
|---|
 |
| As transições para transferir estão no ciclo superior, aceitar no direito e reduzir no inferior. |
O APR replica os passos (informais) do analisador sintático. A computação de $abb\#$ pelo APR é:
$$ \begin{array}{c|rl|l|l} \text{Estado} & \text{Pilha} & \text{Entrada} & \text{Transição} & \text{Ação}\cr \hline p_I & \nil & abb\# & \nil, \nil/\q{0} & \text{iniciar}\ (p_I \tr p) \cr p & \q{0} & abb\# & \nil, \q{0}/\q{1}X\q{0} & \text{reduzir}\ X\to\nil \cr p & \q{1}X\q{0} & abb\# & a, \q{1} / \q{4}a\q{1} & \text{transferir} \cr p & \q{4}a\q{1}X\q{0} & bb\# & b, \q{4} / \q{5}b\q{4} & \text{transferir} \cr p & \q{5}b\q{4}a\q{1}X\q{0} & b\# & \nil, \q{5}b\q{4}/\q{6}Y\q{4} & \text{reduzir}\ Y\to b \cr p & \q{6}Y\q{4}a\q{1}X\q{0} & b\# & \empty & \text{rejeitar} \end{array} $$ e pára porque atinge uma configuração sem transições definidas (o topo é $\q{6}$ e o símbolo da entrada é $b$). Por outro lado a computação de $aabaa\#$ é: $$ \begin{array}{c|rl|l|l} \text{Estado} & \text{Pilha} & \text{Entrada} & \text{Transição} & \text{Ação}\cr \hline p_I & \nil & aabaa\# & \nil, \nil/\q{0} & \text{iniciar}\ (p_I \tr p) \cr p & \q{0} & aabaa\# & \nil, \q{0}/\q{1}X\q{0} & \text{reduzir}\ X\to\nil \cr p & \q{1}X\q{0} & aabaa\# & a, \q{1} / \q{4}a\q{1} & \text{transferir} \cr p & \q{4}a\q{1}X\q{0} & abaa\# & a, \q{4} / \q{4}a\q{4} & \text{transferir} \cr p & \q{4}a\q{4}a\q{1}X\q{0} & baa\# & b, \q{4} / \q{5}b\q{4} & \text{transferir} \cr p & \q{5}b\q{4}a\q{4}a\q{1}X\q{0} & aa\# & \nil, \q{5}b\q{4}/\q{6}Y\q{4} & \text{reduzir}\ Y\to b \cr p & \q{6}Y\q{4}a\q{4}a\q{1}X\q{0} & aa\# & a, \q{6} / \q{7}a\q{6} & \text{transferir} \cr p & \q{7}a\q{6}Y\q{4}a\q{4}a\q{1}X\q{0} & a\# & \nil, \q{7}a\q{6}Y\q{4}a\q{4}/\q{6}Y\q{4} & \text{reduzir}\ Y\to aYa \cr p & \q{6}Y\q{4}a\q{1}X\q{0} & a\# & a, \q{6} / \q{7}a\q{6} & \text{transferir} \cr p & \q{7}a\q{6}Y\q{4}a\q{1}X\q{0} & \# & \nil, \q{7}a\q{6}Y\q{4}a\q{1}/\q{3}Y\q{1} & \text{reduzir}\ Y\to aYa \cr p & \q{3}Y\q{1}X\q{0} & \# & \nil,\q{3}Y\q{1}X\q{0}/ \q{1} X \q{0} & \text{reduzir}\ X\to XY \cr p & \q{1}X\q{0} & \# & \#, \q{1} / \q{2}\#\q{1} & \text{transferir} \cr p & \q{2}\#\q{1}X\q{0} & \nil & \nil, \q{2}\# \q{1} X \q{0}/\nil & \text{aceitar}\ S\to X \# \cr p & \nil & \nil & \end{array} $$ e termina numa configuração com um estado final e com a pilha e a entrada ambas vazias. Neste caso, lendo em reverso as produções obtém-se a derivação direita da palavra dada: $$ S \nderR{S \to X\#} X\# \nderR{X \to XY} XY \# \nderR{Y \to aYa} XaYa\# \nderR{Y \to aYa} XaaYaa\# \nderR{Y \to b} Xaabaa\# \nderR{X \to \nil} aabaa\# $$
Este exemplo ilustra o tratamento “automático” da análise sintática das gramáticas LR(k).
- Dada uma GIC, a construção do AIV e a respetiva TAS permite determinar se a GIC é, ou não LR(0).
- Se o for, a TAS é usada para construir o APR que reconhece a linguagem gerada pela GIC.
- Além disso, o processamento de uma palavra aceite pelo APR permite encontrar a derivação direita dessa palavra.
- Em todo este processo, desde a construção do AIV e da TAS, do APR e a computação de palavras os algoritmos são eficientes (isto é, o número de passos é polinomial no tamanho do input.)
Resta saber se as gramáticas LR(0) são adequadas.
Considerando a seguinte gramática de expressões algébricas simplificadas:
$$ \begin{aligned} S &\to E\# \cr E &\to E + T \alt T \cr T &\to T \times F \alt F \cr F &\to n \alt (E) \end{aligned} $$
Na construção do AIV desta GIC o estado inicial tem os seguintes itens:
$$ \begin{aligned} &\q{0} \cr \hline S &\to \cdot E \# \cr \hline E &\to \cdot E + T \cr E &\to \cdot T \cr T &\to \cdot T \times F \cr \vdots \end{aligned} $$
Deste estado sai uma aresta $T$ que leva a um novo estado com os seguintes itens $$ \begin{aligned} &\q{?} \cr \hline E &\to T \cdot & \star\cr T &\to T \cdot \times F \cr \vdots \end{aligned} $$ onde existe um conflito redução/transferência (a redução de $E \to T$ com a transferência de $\times$).
Este exemplo mostra que as gramáticas LR(0) são demasiado simples para definir expressões algébricas e portanto não são adequadas para definir as linguagens de programação.
A solução para este problema consiste em “adaptar” a ideia das gramática LL(1), considerando os símbolos de avanço, ao processo das gramáticas LR(0).
Conclusão
- O que conseguimos resolver
- O que falta resolver.
Gramáticas LR(1)
Gerador de Analisador Sintático a partir da GIC.
Embora as gramáticas LR(0) proporcionem um algoritmo completo e eficiente para a análise sintática, as linguagens abrangidas não incluem expressões algébricas, pelo que é necessário considerar um esquema mais adequado.
Aqui que entram as gramáticas LR(1), que usam informação sobre o “proximo terminal não processado” (o avanço) para guiar o processo da análise sintática.
Item LR(1)
Seguindo a estrutura da apresentação das gramáticas LR(0), define-se:
- Itens, Itens Válidos e Fecho de um conjunto de itens.
- Autómato dos itens válidos.
- Condições LR(1).
- Tabela de Análise Sintática.
- Autómato de Pilha Reconhecedor.
Item LR(1). Item LR(1) Válido. Seja $G = \del{V, \Sigma, P, S}$ uma GIC.
Um Item LR(1) de $G$ tem a forma $$\del{A \to u\cdot v \isep L}$$ onde:
- núcleo $A\to u\cdot v$ é um item LR(0).
- símbolos de avanço $L\subseteq \Sigma \cup \set{\#}$.
O item LR(1) $\del{A\to u\cdot v\isep L}$ é válido para $xu$ se, para cada $a\in L$ existe uma derivação $$S \iderR xAy$$ com $a \in \primeiros\at{y\#}$.
O fecho de um conjunto de itens afeta os símbolos de avanço.
O Fecho LR(1) de um conjunto $X$ de itens LR(1) define-se recursivamente:
- base $X \subseteq \fechoI\at{X}$.
- passo Se $\del{A \to u\cdot B\alert{v}\isep L} \in \fechoI\at{X}, B \in V$ então, para cada produção $B \to w$ também $$\del{B\to \cdot w\isep K} \in \fechoI\at{X}$$ onde $$K = \begin{cases} \primeiros\at{\alert{v}} \cup L &\alert{v \ider \nil} \cr \primeiros\at{\alert{v}} &\text{caso contrário}\end{cases}$$
- fecho nada mais pertence a $\fechoI\at{X}$.
Por exemplo, dada a GIC $$ \begin{aligned} S &\to AbA \cr A &\to Aa \alt \nil \end{aligned} $$ tem-se $$ \begin{aligned} \fechoI\at{S\to Ab\cdot A \isep \set{\#}} &= \set{\del{S\to Ab\cdot A \isep \set{\#}}} \cr &\cup \set{\del{A \to \cdot Aa \isep \set{\#}}, \del{A \to \cdot \isep \set{\#}}} \cr &\cup \set{\del{A \to \cdot Aa \isep \set{a}}, \del{A \to \cdot \isep \set{a}}} \cr &= \begin{Bmatrix} S\to Ab\cdot A \isep \# \cr \hline A \to \cdot Aa \isep \# \cr A \to \cdot \isep \# \cr A \to \cdot Aa \isep a \cr A \to \cdot \isep a \end{Bmatrix} \end{aligned} $$
Autómato Finito dos Itens LR(1) Válidos
Tal como nas gramáticas LR(0), os itens LR(1) válidos são reconhecidos por um AFD.
Autómato dos Itens LR(1) Válidos (AIV). Seja $G = \del{V, \Sigma, P, S}$ uma GIC qualquer e $$G’ = \del{V \cup \set{S’}, \Sigma, P \cup \set{S’ \to S}, S’}.$$
O autómato dos itens LR(1) válidos de $G’$ é o AFD $A = \del{Q, V \cup \Sigma, \delta, \q{0}, Q \setminus\set{\empty}}$ tal que:
- estado inicial $\q{0} = \fechoI\at{S’ \to S \isep \#}$.
- transição Para cada $q \in Q, \alert{x} \in V \cup \Sigma$,
$$\delta\at{q, \alert{x}} = \fechoI\at{\set{\del{A \to u\alert{x \cdot} v \isep L} \st \del{A \to u \alert{\cdot x} v \isep L} \in q}}.$$
Por exemplo, para a GIC dada acima:
| Diagrama do Autómato dos Itens LR(1) Válidos |
|---|
 |
| Em cada estado os itens completos são assinalados com $\star$. O estado $\empty$ não está representado. |
O cálculo de $\fechoI\at{S’ \to \cdot S\isep \#}$ passo-a-passo:
- Como ocorre $\alert{\cdot S}$, é necessário adicionar os itens iniciais de $S$. O núcleo é $S\to \cdot AbA$.
- Para calcular o avanço deste item, note-se que inicialmente $(S’ \to \cdot S\alert{\overbrace{\nil}^{v}}\isep \overbrace{\#}^L)$ portanto, pela definição de $\fechoI$, $K= \primeiros\at{\nil} \cup L = \empty \cup \set{\#} = \set{\#}$.
- Portanto, o item LR(1) a acrescentar em $\q{0}$ é $S \to \cdot AbA \isep \#$.
- Agora, de $S \to \alert{\cdot A}bA\isep \#$ é preciso acrescentar os itens iniciais de $A$. Os núcleos são $A \to \cdot Aa$ e $A \to \cdot$. O cálculo dos avanços é idêntico para estes dois itens.
- Estes itens resultam de $S \to \alert{\cdot A \overbrace{b}^v}A\isep \#$. Pela definição de $\fechoI$, $K = \primeiros\at{b} = \set{b}$.
- Portanto, são acrescentados dois itens LR(1): $A \to \cdot Aa\isep b$ e $A \to \cdot \isep b$.
- Do item $A \to \alert{\cdot A \overbrace{a}^{v}} \isep b$, pelas razões anteriores, é necessário acrescentar dois itens LR(1): $A \to \cdot Aa\isep a$ e $A \to \cdot \isep a$.
- Torna a acontecer $A \to \alert{\cdot A \overbrace{a}^{v}} \isep a$ mas os itens que resultam já constam no $\fechoI$ e nada mais é acrescentado.
- Finalmente o fecho tem vários itens com o mesmo núcleo e que diferem apenas no avanço. Neste caso esses itens “fundem-se” num único, unindo os avanços:
- $A \to \cdot Aa\isep b$ e $A \to \cdot Aa\isep a$ fundem-se em $A \to \cdot Aa\isep ab$.
- $A \to \cdot \isep b$ e $A \to \cdot \isep a$ fundem-se em $A \to \cdot \isep ab$.
Tabela de Análise Sintática LR(1)
Tal como no caso das gramáticas LR(0), os estados do AIV LR(1) permitem determinar se o processo da análise sintática pode, ou não, ser aplicado.
Para que a análise sintática seja determinista é necessário que os estados sejam livres de conflitos (redução/redução e redução/transferência). No caso das gramáticas LR(0), sem informação sobre os avanços, cada estado do AIV pode determinar ou uma única redução ou uma transferência. Nos AIV das gramáticas LR(1) os itens têm avanços, que proporcionam decisões mais informadas em cada caso.
No AIV acima, visto como um AIV LR(0), o estado $\q{5}$ tem um conflito redução/transferência. Mas o avanço do item $S \to AbA\isep \#$ restringe a aplicação da redução apenas quando o avanço na entrada é $\#$. Portanto não há conflito com uma eventual transferência de $a$.
Em cada estado, cada avanço identifica a ação (reduzir, transferir, aceitar, rejeitar) no processo da análise sintática.
Portanto, a tabela de análise sintática LR(1) tem uma ação possível para cada símbolo terminal. Especificamente:
Tabela de Análise Sintática LR(1). (TAS LR(1)) Dada uma GIG e o seu AIV LR(1), a tabela de análise sintática LR(1) tem:
- Para cada estado do AIV LR(1), uma linha, exceto para o estado $\empty$.
- Para cada símbolo $\del{V \cup \Sigma}\setminus\set{S’}$, uma coluna que descreve a transição do AIV.
- Para cada símbolo $a \in \Sigma \cup \set{\#}$, uma coluna que, cruzada com a linha do estado $\q{q}$, determina a ação:
- aceitar (ou $A$) se $\q{q}$ contém um item completo de $S’$ e se $a = \#$.
- transferir (ou $T$) se $\q{q}$ contém um item $A \to u \cdot a v\isep L$.
- reduzir (ou $R: A \to p$) se $\q{q}$ contém o item completo $A \to p\cdot\isep L$, $A \not= S$ e $a \in L$.
- rejeitar (omitido).
Por exemplo, A TAS LR(1) do exemplo acima é:
$$ \begin{array}{r|cccc||ccc} \q{q} & S & A & a & b & a & b & \# \cr \hline \q{0} & \q{1} & \q{2} & & & A \to \nil & A \to \nil & \cr \q{1} & & & & & & & \text{aceitar} \cr \q{2} & & & \q{3} & \q{4} & \text{transferir} & \text{transferir} & \cr \q{3} & & & & & A \to Aa & A \to Aa & \cr \q{4} & & \q{5} & & & A \to \nil & & A \to \nil \cr \q{5} & & & \q{6} & & \text{transferir} & & S \to AbA \cr \q{6} & & & & & A \to Aa & & A \to Aa \cr \end{array} $$
Comparando esta tabela com as obtidas nas TAS LR(0), a coluna ação é mais específica, considerando agora os símbolos de avanço e, portanto, a ação depende não só do estado no AIV mas também do próximo símbolo na entrada.
Numa TAS LR(1) mantém-se a necessidade de determinar, sem ambiguidade, cada ação no processo da análise sintática. Em relação ao caso LR(0), a escolha da ação depende não só do estado do AIV mas também do símbolo de avanço.
Quando esta informação (estado AIV + símbolo de avanço) não é suficiente para determinar uma única ação tem-se um conflito, que pode ser de dois tipos:
- Conflito Redução/Redução LR(1): Num estado com dois itens completos em que os avanços se intersetam. Formalmente, se no AIV LR(1) existe um estado com dois itens completos distintos $\del{A \to p\cdot \isep L}$ e $\del{B \to q\cdot \isep K}$ e $L \cap K \not= \empty$.
- Conflito Redução/Transferência LR(1): Num estado com um item completo em que sai uma aresta “com um terminal” que está no avanço desse item completo. Formalmente, se no AIV LR(1) existe um item completo $\del{A \to p \cdot \isep L}$ e um item $\del{B \to u \cdot a v \isep L}$ e $a \in L$.
Teorema das Gramáticas LR(1). Uma GIC é LR(1) se e só se o seu AIV não tem conflitos redução/redução LR(1) nem redução/transferência LR(1).
Autómato de Pilha Reconhecedor LR(1)
Quando o AIV LR(1) de uma GIC está livre de conflitos é possível definir-se um autómato de pilha para reconhecer a linguagem gerada pela GIC. Além disso, para as palavras geradas/aceites, a observação da computação permite recuperar a derivação direita da respetiva palavra.
Autómato de Pilha Reconhecedor LR(1). Seja $G=(V, \Sigma, P, S)$ uma GIC LR(1) e $A = (Q, V\cup \Sigma, \delta_A, \q{0}, Q \setminus \set{\empty})$ o seu AIV LR(1). O Autómato de Pilha Reconhecedor LR(1) (APR LR(1)) de $G$, que reconhece a linguagem gerada por $G$, é $$R = \del{Q_R, \Sigma \cup \set{\#}, V \cup \Sigma \cup Q \setminus \set{\empty}, \delta, p_I, F_R}$$ com
- estados de controlo: $Q_R = \set{p_I, p} \cup \set{p_a \st a \in \Sigma \cup \set{\#}}$.
- estados finais: $F_R = \set{p_{\#}}$.
e em que a transição, $\delta$, é definida pelos seguintes elementos:
- iniciar: $\alert{\del{p, \q{0}} \in \delta\at{p_I, \nil, \nil}}$.
- avançar: Para cada $a \in \Sigma \cup \set{\#}$ então $\alert{\del{p_a, \nil} \in \delta\at{p, a, \nil}}$.
- transferir: Para cada $q \in Q$ com um item $\del{A \to u\cdot a v\isep L}$ em que $a \in \Sigma$ e $q’ = \delta_A\at{q, a}$ então $\alert{\del{p, q’ a q} \in \delta\at{p_a, \nil, q}}$.
- reduzir: Para cada estado $q \in Q$ com um item completo $\del{A \to a_1 a_2 \cdots a_n\cdot \isep L}$ com $A \not= S’$ e para cada $a \in L$, quando no AIV existe a computação $$q_0 \trf{a_1} q_1 \trf{a_2} q_2 \cdots \trf{a_n} q_n = q$$ e $q’ = \delta_A\at{q_0, A}$ então $\alert{\del{p_a, q’ A q_0} \in \delta\at{p_a, \nil, q_n a_n \cdots q_2 a_2 q_1 a_1 q_0}}$.
- aceitar: Para cada estado $q \in Q$ com um item completo $\del{S’ \to a_1 a_2 \cdots a_n\cdot \isep L}$ do símbolo inicial da GIC, se $\# \in L$ e quando no AIV existe a computação $$\q{0} \trf{a_1} q_1 \trf{a_2} \cdots \trf{a_n} q_n = q$$ então $\alert{\del{p_{\#}, \nil} \in \delta\at{p_{\#}, \nil, q_n a_n \cdots q_2 a_2 q_1 a_1 \q{0}}}.$
Alternativamente as transições do APR LR(1) podem ser descritas pela seguinte tabela: $$ \begin{array}{l||l|lcr} \text{Operação} & \text{Condição} & \text{De} & \text{Aresta} & \text{Para} \cr \hline \text{Iniciar}\cr & & p_I & \nil, \nil/\q{0} & p \cr \cr \hline \text{Avançar}\cr &a \in \Sigma \cup \set{\#} & p & a, \nil/\nil & p_a \cr \cr \hline \text{Transferir}\cr & \del{A \to u \cdot a v \isep L} \in q & p_a & \nil, q / q’ a q & p \cr & a \in \Sigma \cr\cr & q’ = \delta_A\at{q, a} \cr \cr \hline \text{Reduzir}\cr &\del{A \to a_1 \cdots a_n\cdot \isep L} \star \in q & p_a & \nil, \alpha / \beta & p_a \cr & A \not= S’ \cr & a \in L \cr \cr & q_0 \trf{a_1} \cdots \trf{a_n} q_n, q_n = q \cr & \alpha = q_n a_n \cdots a_1 q_0 \cr \cr & q_0 \trf{A} q’ \cr & \beta = q’ A q_0 \cr \cr \hline \text{Aceitar}\cr &\del{S’ \to a_1 \cdots a_n\cdot \isep L}\star \in q & p_{\#} & \nil, \alpha / \nil & p_{\#} \cr & \# \in L \cr \cr & \q{0} \trf{a_1} \cdots \trf{a_n} q_n, q_n = q \cr & \alpha = q_n a_n \cdots a_1 \q{0} \end{array} $$
Intuitivamente os estados do APR LR(1) refinam os do APR LR(0) com informação sobre o avanço. O estado $p$ “consulta” o símbolo de avanço (por exemplo, $a$) e encaminha a computação para o respetivo estado $p_a$, onde os passos são feitos sob o pressuposto “o avanço é $a$”.
A computação fica em $p_a$ até $a$ ser transferido da entrada para a pilha. Depois dessa transferência é necessário tornar a consultar o avanço (em $p$) e proceder de acordo com o novo avanço.
O símbolo $\#$ marca o fím da entrada e é processado de acordo com esse pressuposto. Por exemplo, não há transições de $p_{\#}$ para $p$ e só neste estado pode ocorrer a ação aceitar.
Continuando o exemplo anterior, a transição do APR LR(1) tem as seguintes arestas:
- iniciar transições $p_I \tr p$: $\nil, \nil/\q{0}$.
- avançar $$ \begin{array}{c|lcl} \text{terminal} & \text{de} & \text{aresta} & \text{para} \cr \hline a & p & a, \nil/\nil & p_a \cr b & p & b, \nil/\nil & p_b \cr \# & p & \#, \nil/\nil & p_{\#} \end{array} $$
- transferir $$ \begin{array}{l|lcl} \text{AIV} & \text{APR: de} & \text{APR: aresta} & \text{APR: para}\cr \hline \q{2} \trf{a} \q{3} & p_a & \nil, \q{2}/\q{3}a\q{2} & p \cr \q{2} \trf{b} \q{4} & p_b & \nil, \q{2}/\q{4}b\q{2} & p \cr \hline \q{5} \trf{a} \q{6} & p_a & \nil, \q{5}/\q{6}a\q{5} & p \end{array} $$
- reduzir $$ \begin{array}{llll|r} \text{AIV: estado} & \text{AIV: item completo de}\ A\not= S’ & \text{AIV: avanços} & \text{AIV: computação} & \text{APR: aresta} \cr \hline \q{0} & A \to \nil \cdot & a, b & \q{0} & \nil, \q{0}/\q{2}A\q{0} \cr \hline \q{3} & A \to Aa \cdot & a, b & \q{0} \trf{A} \q{2} \trf{a} \q{3} & \nil,\q{3}a\q{2}A\q{0}/ \q{2} A \q{0} \cr \hline \q{4} & A \to \nil \cdot & \#, a & \q{4} & \nil, \q{4}/ \q{5} A \q{4} \cr \hline \q{5} & S \to AbA \cdot & \# & \q{0} \trf{A} \q{2} \trf{b} \q{4} \trf{A} \q{5} & \nil, \q{5}A\q{4}b\q{2} A \q{0}/ \q{1} S \q{0} \cr \hline \q{6} & A \to Aa \cdot & \#, a & \q{4} \trf{A} \q{5} \trf{a} \q{6} & \nil, \q{6} a \q{5} A \q{4} / \q{5} A \q{4} \end{array} $$
- aceitar $$ \begin{array}{llll|r} \text{AIV: estado} & \text{AIV: item completo de}\ S’ & \text{AIV: avanços} & \text{AIV: computação} & \text{APR: aresta} \cr \hline \q{1} & S’ \to S \cdot & \# & \q{0} & \nil, \q{1}S\q{0}/\nil \end{array} $$
que corresponde ao diagrama
| Diagrama do APR LR(1) |
|---|
 |
| As arestas $p \to p_x$ são avançar, $p_x \to p_x$ reduzir e aceitar e $p_x \to p$ são transferir. |
Como é que este APR processa palavras? Por exemplo, $aba$ é gerada pela GIC, enquanto que $bab$ não.
Para $aba$ o APR tem a computação $$ \begin{array}{c|rl|ll|l} \text{estado} & \text{pilha} & \text{entrada} & \text{próximo estado} & \text{aresta} & \text{ação}\cr \hline p_I & \nil & aba\# & p & \nil, \nil/\q{0}& \text{iniciar} \cr p & \q{0} & aba\# & p_a & a, \nil/\nil& \text{avançar} \cr p_a & \q{0} & ba\# & p_a & \nil, \q{0}/\q{2}A\q{0}& \text{reduzir }A \to \nil \cr p_a & \q{2}A\q{0} & ba\# & p & \nil, \q{2}/\q{3}a\q{2}& \text{transferir}\cr p & \q{3}a\q{2}A\q{0} & ba\# & p_b & b, \nil/\nil& \text{avancar}\cr p_b & \q{3}a\q{2}A\q{0} & a\# & p_b & \nil, \q{3}a\q{2}A\q{0}/\q{2}A\q{0}& \text{reduzir }A \to Aa\cr p_b & \q{2}A\q{0} & a\# & p & \nil, \q{2}/\q{4}b\q{2}& \text{transferir}\cr p & \q{4}b\q{2}A\q{0} & a\# & p_a & a, \nil/\nil& \text{avançar}\cr p_a & \q{4}b\q{2}A\q{0} & \# & p_a & \nil, \q{4}/\q{5}A\q{4}& \text{reduzir }A \to \nil\cr p_a & \q{5}A\q{4}b\q{2}A\q{0} & \# & p & \nil, \q{5}/\q{6}a\q{5}& \text{transferir}\cr p & \q{6}a\q{5}A\q{4}b\q{2}A\q{0} & \# & p_{\#} & \#, \nil/\nil& \text{avançar}\cr p_{\#} & \q{6}a\q{5}A\q{4}b\q{2}A\q{0} & \nil & p_{\#} & \nil, \q{6}a\q{5}A\q{4}/\q{5}A\q{4}& \text{reduzir }A\to Aa\cr p_{\#} & \q{5}A\q{4}b\q{2}A\q{0} & \nil & p_{\#} & \nil, \q{5}A\q{4}b\q{2}A\q{0}/\q{1}S\q{0}& \text{reduzir }S\to AbA\cr p_{\#} & \q{1}S\q{0} & \nil & p_{\#} & \nil, \q{1}S\q{0}/\nil& \text{aceitar }(S’\to S) \cr p_{\#} & \nil & \nil \cr \end{array} $$ que aceita e mostra a derivação $S \derR AbA \derR AbAa \derR Aba \derR Aaba \derR aba$. Quando à computação de $bab$, rejeita:
$$ \begin{array}{c|rl|ll|l} \text{estado} & \text{pilha} & \text{entrada} & \text{próximo estado} & \text{aresta} & \text{ação}\cr \hline p_I & \nil & bab\# & p & \nil, \nil/\q{0}& \text{iniciar} \cr p & \q{0} & bab\# & p_b & b, \nil/\nil& \text{avançar} \cr p_b & \q{0} & ab\# & p_b & \nil, \q{0}/\q{2}A\q{0}& \text{reduzir}\ A\to \nil \cr p_b & \q{2}A\q{0} & ab\# & p & \nil, \q{2}/\q{4}b\q{2}& \text{transferir}\cr p & \q{4}b\q{2}A\q{0} & ab\# & p_a & a, \nil/\nil& \text{avançar}\cr p_a & \q{4}b\q{2}A\q{0} & b\# & p_a & \nil, \q{4}/\q{5}A\q{4}& \text{reduzir}\ A\to \nil\cr p_a & \q{5}A\q{4}b\q{2}A\q{0} & b\# & p & \nil, \q{5}/\q{6}a\q{5}& \text{transferir}\cr p & \q{6}a\q{5}A\q{4}b\q{2}A\q{0} & b\# & p_b & \nil, \nil/\nil& \text{avançar}\cr p_b & \q{6}a\q{5}A\q{4}b\q{2}A\q{0} & \# & \empty & \empty & \text{rejeitar} \end{array} $$
Com este exemplo termina a resolução do Problema Principal de ALP — Dada uma linguagem $A$ e uma palavra $p$ no mesmo alfabeto, determinar se $p \in A$ de forma computável, eficiente e adequada.
- A linguagem é adequada se for formalmente definida por uma GIC LR(1).
- Dada uma GIC que gere a linguagem, a construção algorítmica do seu AIV LR(1) é eficiente.
- Pode-se verificar algoritmicamente e de forma eficiente se a GIC é LR(1), confirmando que nenhum estado do seu AIV LR(1) tem contradições. Nesse caso a linguagem é adequada.
- A construção do APR LR(1) a partir do AIV LR(1) é, também, algorítmica e eficiente.
- Dada uma palavra sobre o alfabeto da linguagem, o processamento pelo APR LR(1) é eficiente (e, claro, algorítmico). Adicionalmente, se a palavra está na linguagem, é possível recuperar a sua derivação na GIC para efeitos de processamento semântico.
Resumindo, este processo define um algoritmo (qua pode ser implementado em qualquer linguagem de programação comum) que é eficiente e resolve o Problema Principal de ALP.
Gramáticas LALR(1)
Neste ponto é fácil melhorar o seguinte problema: a construção do AIV gera muitos estados, o que pode ter um efeito negativo no desempenho dos restantes passos.
Quando dois estados do AIV têm os mesmos núcleos e, eventualmente, avanços distintos, a fusão consiste em juntar esses dois estados num único, cujos itens são obtidos:
- os núcleos são os mesmos;
- cada avanço é a união dos avanços dos itens correspondentes.
Usando um exemplo anterior
| Diagrama do Autómato dos Itens LR(1) Válidos |
|---|
 |
| Os estados $\q{3}$ e $\q{6}$ têm exatamente os mesmos núcleos. |
O amalgamento deste AIV é
| Autómato Amalgamado |
|---|
 |
| O estado $\q{36}$ resulta de fundir $\q{3}$ com $\q{6}$. Neste exemplo não há mais fusões possíveis. |
Formalmente:
Autómato Amalgamado. Seja $A = \del{Q, \Sigma, \delta, \q{0}, F}$ um AIV LR(1).
Se $X = \set{q_1, \ldots, q_n}$ for um conjunto de estados de $A$ com os mesmos núcleos, a fusão destes estados é o estado $\widehat{X}$ com os itens $\del{A \to u\cdot v \isep L_1 \cup \cdots L_n}$ tais que $\del{A \to u \cdot v \isep L_i} \in q_i$.
Seja $\set{Q_1, \ldots, Q_n}$ uma partição de $Q$ tal que:
- todos os estados de $Q_i$ têm os mesmos núcleos e
- se $i \not= j$ os núcleos dos estados de $Q_i$ e $Q_j$ são disjuntos. então
O autómato amalgamado $A’$ é o autómato que resulta de fundir os estados com o mesmo conjunto de núcleos: $$A’ = \del{Q_A, \Sigma, \delta’, \widehat{\set{\q{0}}}, Q_A\setminus\set{\widehat{\set{\empty}}} }$$ com
- estados de controlo $Q_A = \set{\widehat{Q_1}, \ldots, \widehat{Q_n}}$.
- transição $\delta’\at{\widehat{Q_i}, a} = \widehat{Q_j}$ se existe $q \in Q_i$ tal que $\delta\at{q, a} \in Q_j$.
Os autómatos amalgamados definem uma classe de gramáticas distinta de LR(1):
Gramática LALR(1). Uma GIC é LALR(1) se o seu autómato amalgamado satisfaz as condições LR(1): não tem conflitos redução/redução nem redução/transferência.
O principal interesse das gramáticas LALR(1) é, essencialmente, prático: Intuitivamente, são as gramáticas com “bons” AIV depois de amalgamados.
Exercícios — Análise Sintática
Os exercícios assinalados com “✓” serão resolvidos nas aulas práticas; Os assinalados com “†” têm elevada dificuldade. Todos os restantes devem ser resolvidos pelos alunos.
Limpeza de uma Gramática
Exercício 01
Considere a gramática independente do contexto $$ G = (\left\lbrace S,B,C \right\rbrace, \left\lbrace a,b,c \right\rbrace, P, S) $$ com produções $$ \begin{aligned} S &\to aS \ |\ bS \ |\ B \cr B &\to bb \ |\ C \ |\ \lambda \cr C &\to cC \ |\ \lambda \end{aligned} $$
- Escreva uma expressão regular que represente a linguagem gerada por $G$.
- Construa uma gramática (essencialmente) não contraível equivalente.
- Elimine as produções unitárias da gramática obtida na alínea anterior.
Exercício 02
Repita o exercício anterior para a gramática:
-
$G = (\left\lbrace S,A,B,C \right\rbrace, \left\lbrace a,b,c \right\rbrace, P, S)$ com produções
$$ \begin{aligned} S &\to ABC \alt \nil \cr A &\to aA \alt a \cr B &\to bB \alt A \cr C &\to cC \alt \nil \end{aligned} $$
-
$G = (\left\lbrace S,A,B \right\rbrace, \left\lbrace a,b \right\rbrace, P, S)$ com produções
$$ \begin{aligned} S&\to BSA \alt A \cr A &\to aA \alt \nil \cr B &\to Bba \alt \nil \end{aligned} $$
Exercício 03
Construa uma gramática equivalente a $G = (\left\lbrace S,A,B,C \right\rbrace, \left\lbrace a,b,c \right\rbrace, P, S)$, com produções $$ \begin{aligned} S &\to A \alt B \alt C \cr A &\to aa \alt B \cr B &\to bb \alt C \cr C &\to cc \alt A \end{aligned} $$ que não contenha produções unitárias e escreva uma expressão regular que represente a linguagem gerada por esta gramática.
Exercício 04
Construa uma gramática equivalente a $G = (\set{ S,A,B,C,D,E,F,G }, \set{ a,b }, P, S)$, com produções $$ \begin{aligned} S &\to aA \alt BD \cr A &\to aA \alt aAB \alt aD \cr B &\to aB \alt aC \alt BF \cr C &\to Bb \alt aAC \alt E \cr D &\to bD \alt bC \alt b \cr E &\to aB \alt bC \cr F &\to aF \alt aG \alt a \cr G &\to a \alt b \end{aligned} $$ sem símbolos inúteis e encontre uma expressão regular que represente a linguagem gerada por esta gramática.
Exercício 05
Construa uma gramática equivalente a $G = (\set{ S,A,B,C }, \set{ a,b,c }, P, S)$, com produções $$ \begin{aligned} S &\to aAbB \alt ABC \alt a \cr A &\to aA \alt a \cr B &\to bBcC \alt b \cr C &\to abc \end{aligned} $$ na forma normal de Chomsky.
Exercício 06
✓ Construa uma gramática equivalente a $G = (\set{ E,S,T }, \set{ a,b,- }, P, E)$, com produções $$ \begin{aligned} E &\to S \cr S &\to T \alt S - T \cr T &\to a \alt b \end{aligned} $$ na forma normal de Greibach.
Exercício 07
Repita o exercício anterior para a gramática
- Com produções $$ \begin{aligned} A &\to aAb \alt B \cr B &\to Bb \alt \nil \end{aligned} $$
- Com produções $$ \begin{aligned} S &\to A \alt B \cr A &\to AAA \alt a \alt B \cr B &\to BBb \alt b \end{aligned} $$
Gramáticas LL(k)
Exercício 08
Calcule os símbolos diretores e determine se as seguintes gramáticas são $LL(1)$:
- $G_1 = (\set{S,A,B}, \set{a,b,c,\#}, \set{S \to AB\#, A \to aAb \alt B, B \to aBc \alt \nil}, S)$
- $G_2 = (\set{S,A,B,C}, \set{a,b,c,d,\#}, \set{S \to ABC\#, A \to aA \alt \nil, B \to bBc \alt \nil, C \to cA \alt dB \alt \nil}, S)$
- ✓ $G_3 = (\set{S,A,B,C,D}, \set{a,b,c,d,\#}, \set{S \to aAd\#, A \to BCD, B \to bB \alt \nil, C \to cC \alt \nil, D \to bD \alt \nil}, S)$
Exercício 09
†✓ Modifique a gramática $G = (\set{S,A,B,C}, \set{a,b,c,\#}, P, S)$ de modo a obter uma gramática $LL(1)$ equivalente. As produções de $G$ são: $$\begin{aligned} S &\to A\#\cr A &\to aB \alt Ab \alt Ac\cr B &\to bBc \alt \nil \end{aligned}$$ Sugestão: Comece por determinar $L\at{G}$.
Exercício 10
Repita o exercício anterior para a gramática $$\begin{aligned} S &\to aA\# \alt abB\# \alt abcC\# \cr A &\to aA \alt \nil \cr B &\to bB \alt \nil \cr C &\to Cc \alt \nil \end{aligned}$$
Exercício 11
Defina uma gramática $LL(1)$ que gere a linguagem das expressões aritméticas com subtração, multiplicação e parêntesis. (Use o símbolo $n$ para representar os inteiros.)
Gramáticas LR(0)
Exercício 12
Determine os $\text{contexto-}LR\at{0}$ da gramática com produções
- ✓
$$ \begin{aligned} S &\to aA \alt bB \cr A &\to abA \alt bB \cr B &\to bBc \alt bc \end{aligned} $$
$$ \begin{aligned} S &\to aA \alt aB \cr A &\to aAb \alt b \cr B &\to bBa \alt b \end{aligned} $$
Exercício 13
✓ Considere a gramática $G = (\set{S,A,B}, \set{a,b,\#}, \set{S \to aBA\#, A \to b \alt aB, B \to a \alt bB}, S)$.
- Construa o autómato dos itens válidos de $G$.
- Diga, justificando, se $G$ é $LR(0)$.
- Construa a tabela de análise sintática para $G$.
- Defina o autómato de pilha reconhecedor $LR(0)$ para $G$.
Exercício 14
Repita as duas primeiras alíneas do exercício anterior para a gramática $$G = (\set{S,A,B}, \set{a,b,\#}, \set{S \to aA\# \alt AB\#, A \to aAb \alt b, B \to ab \alt b}, S)$$ Se concluir que a gramática não é $LR(0)$, enumere os conflitos encontrados.
Exercício 15
Repita o exercício anterior para a gramática $$G = (\set{X,Y,Z}, \set{0,1,\#}, \set{X \to ZY\# \alt 1YZ\#, Y \to 0Y \alt \nil, Z \to Z1 \alt 1}, X).$$
Gramáticas LR(1)
Exercício 16
✓ Considere a gramática $G = (\set{S,A,B}, \set{a,b}, P, S)$, com o conjunto de produções: $$\begin{aligned} S &\to AB \cr A &\to aA \alt \nil \cr B &\to Bb \alt \nil \end{aligned}$$
- Construa o autómato dos itens $LR(1)$ válidos de $G$.
- Diga, justificando, se $G$ é $LR(1)$.
- Construa o autómato amalgamado e diga, justificando, se $G$ é $LALR(1)$.
- Construa a tabela de análise sintática $LR(1)$ para $G$.
- Com base no autómato dos itens válidos de $G$, defina o autómato de pilha reconhecedor $LR(1)$.
- Construa a computação do autómato de pilha para a palavra $aabb$.
Resolução em Banda Desenhada
| AIV | TAS | APR |
|---|---|---|
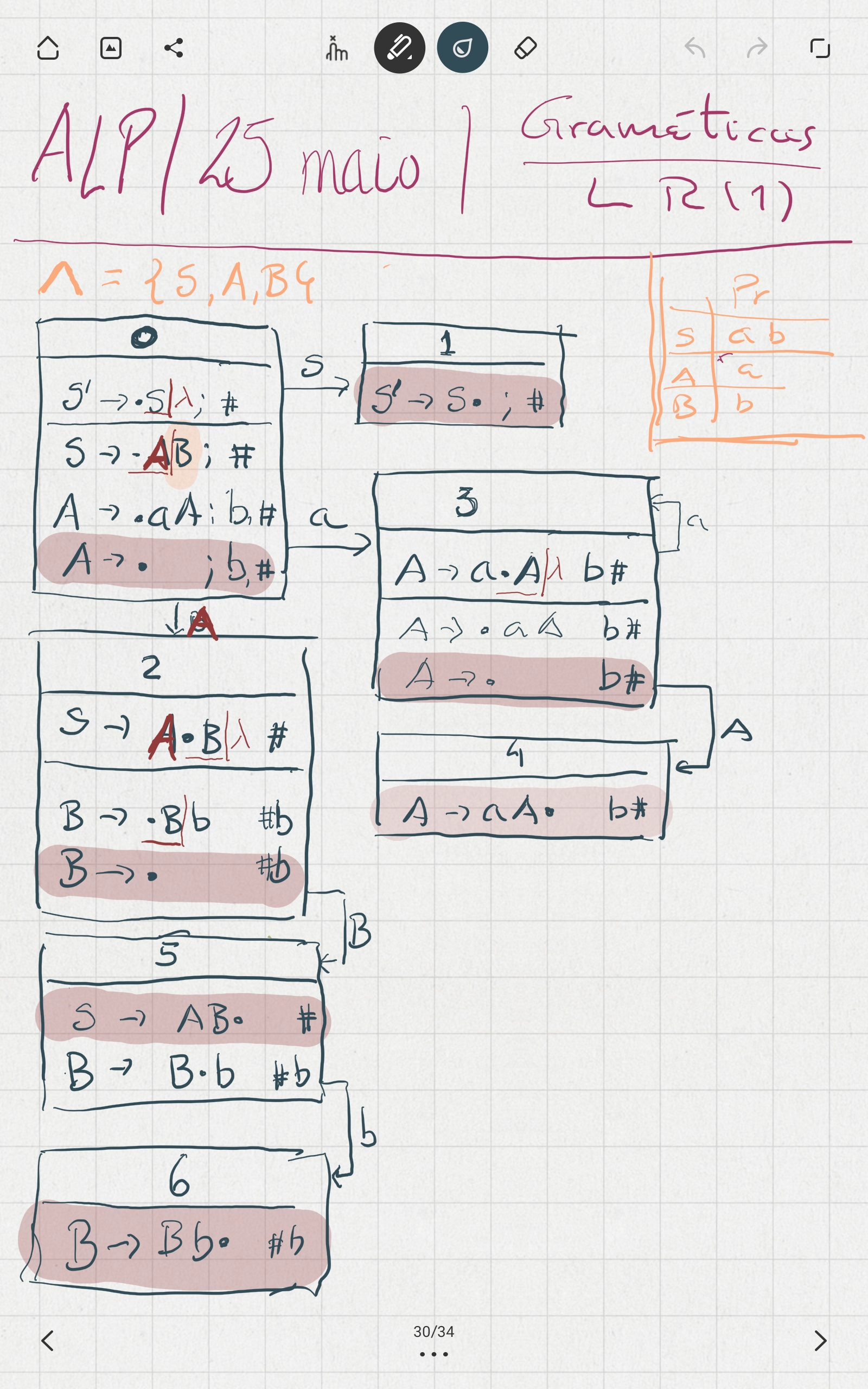 | 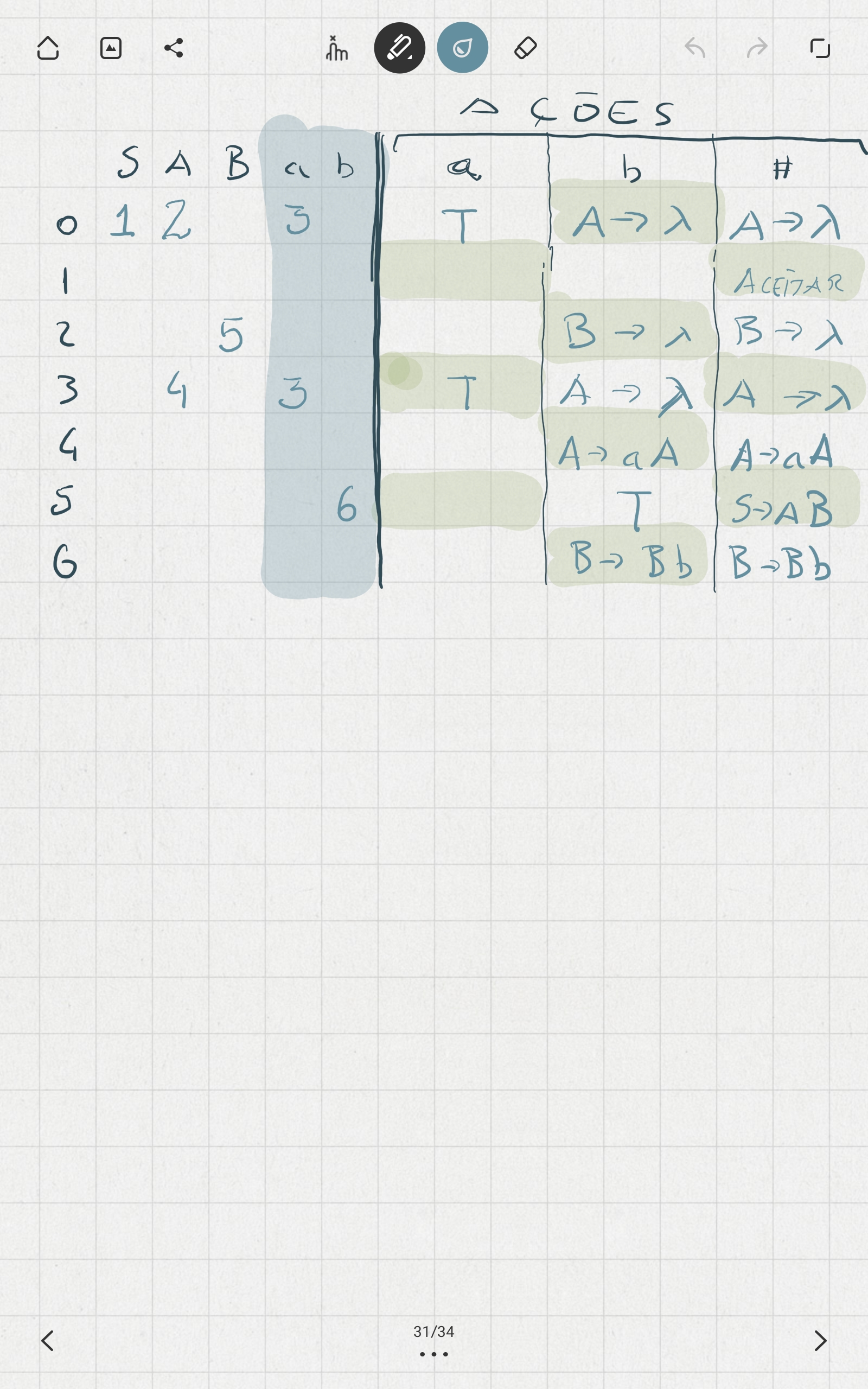 | 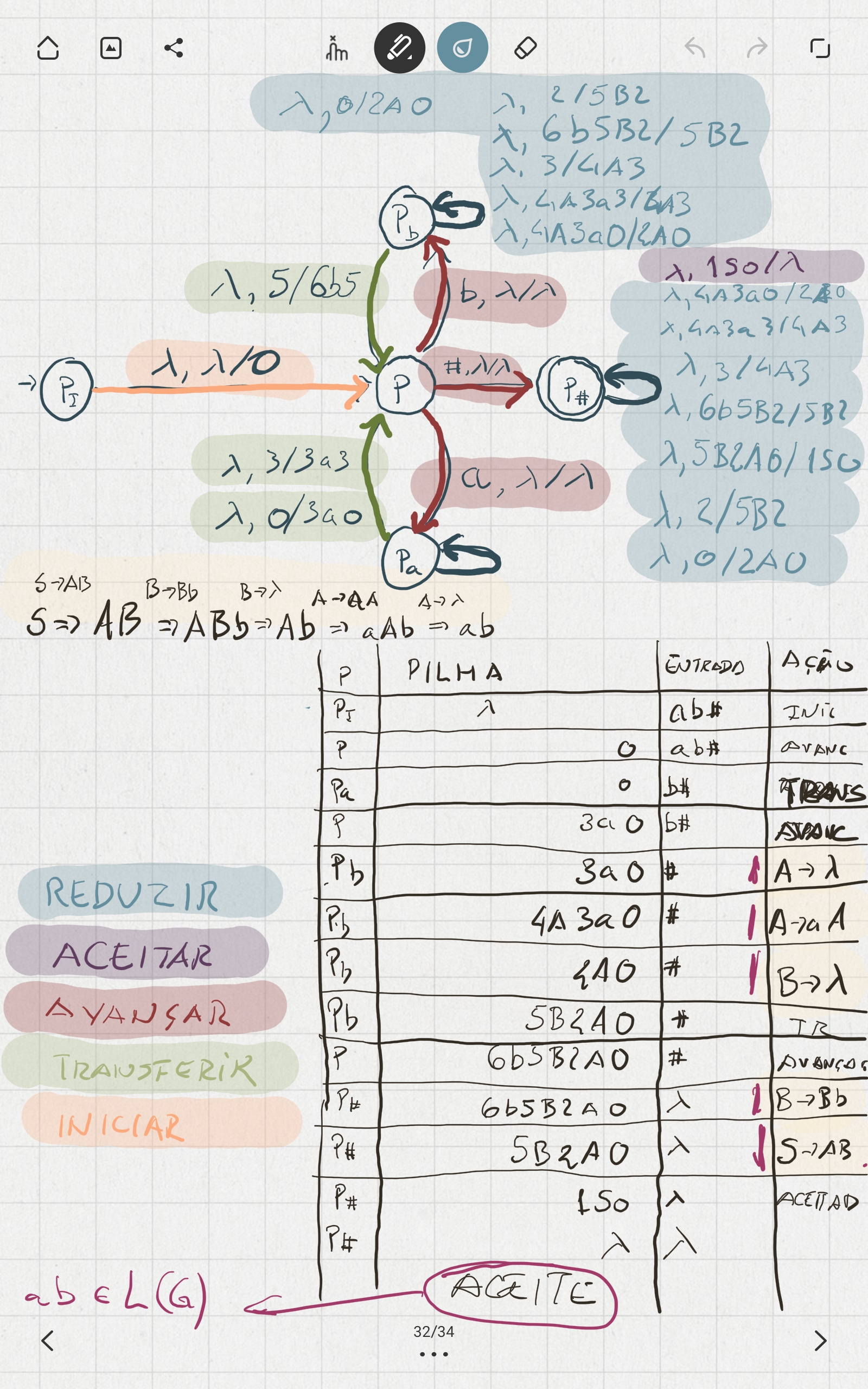 |
Exercício 17
✓ Repita o exercício anterior com a gramática $G = (\set{S,A,B}, \set{a,b}, P, S)$, com o conjunto de produções: $$\begin{aligned} S &\to ABA \cr A &\to Aa \alt \nil \cr B &\to bB \alt b \end{aligned}$$
Exercício 18
✓ Repita as primeiras 4 alíneas do exercício anterior com a gramática $G = (\set{S}, \set{a}, P, S)$, com o conjunto de produções: $$\begin{aligned} S &\to aSa \alt \nil \end{aligned}$$ (Se $G$ não é $LR(1)$, não faça as alíneas que não se aplicam.)
Exercício 19
Repita o exercício anterior com as gramáticas
- $G = (\set{S,E,F}, \set{w,x,y,z}, P, S)$, com o conjunto de produções:
$$\begin{aligned} S &\to Ex \alt yEw \alt Fw \alt yFx \cr E &\to z \cr F &\to z \end{aligned}$$
- $G = (\set{S,C}, \set{c,d}, P, S)$, com o conjunto de produções:
$$\begin{aligned} S & \to CC \cr C & \to cC \alt d \end{aligned}$$
- $G = (\set{E,T}, \set{i,+,(,)}, P, E)$, com o conjunto de produções:
$$\begin{aligned} E &\to E+T \alt T \cr T &\to i \alt (E) \end{aligned}$$
Implementação
As indicações gerais para os exercícios de implementação são válidas aqui.
Uma biblioteca para Grafos Orientados, com Pesquisas
Para este grupo de exercícios pode usar, entre outros, os grafos indicados a seguir.
# Grafos para testar as implementações.
simples = [
(0, 2),
(1, 3),
(2, 0),
(3, 1),
]
cubo = [
(0, 1), (0, 4),
(1, 2), (1, 5),
(2, 3), (2, 6),
(3, 0), (3, 7),
(4, 5), (5, 6), (6, 7), (7, 4)
]
cubo_inclinado = [
(0, 1), (0, 3), (0, 4),
(1, 2), (1, 5),
(2, 6),
(3, 7),
(4, 5), (4, 7),
(5, 6),
(7, 6)
]
- Represente. Uma aresta orientada $a \to b$ por um tuplo
(a, b). - Represente. Um Grafo (orientado) por uma lista de arestas.
- Implemente. A função
nodes(graph)que devolve o conjunto do vértices do grafo. - Implemente. A função
children(graph, node)que devolve o conjunto dos filhos do vérticenode. - Implemente. A função
parents(graph, node)que devolve o conjunto dos pais do vérticenode. - Implemente. A função
is_path(graph, path)que testa sepathé um caminho no grafograph. Um caminho é uma lista de vértices em que dois consecutivos estão ligados por uma aresta. - Implemente. A função
has_loop(graph, path)que testa sepathtem algum ciclo no grafograph. Um ciclo é um caminho que começa e termina no mesmo vértice. - Implemente. A função
search(graph, a, b)de acordo com os apontamentos teóricos. Considere uma variante em que as funçõesexpandejoinsão passadas como argumentos opcionais. Verifique o que acontece se não controlar os vértices visitados. - Teste. Pesquisas ascendentes, descendentes, em largura e em profundidade.
Uma biblioteca para Árvores, com Pesquisas
- Represente. Um nó/vértice é representado pela estrutura
Nodecom atributos:value: Qualquer “coisa” que pode estar no nó.- Obs. nem todas as linguagens permitem isto facilmente. Em
pythonekotlin, por exemplo, é direto.
- Obs. nem todas as linguagens permitem isto facilmente. Em
children: Uma lista deNode.- Obs. esta recursividade também levanta problemas em algumas linguagens. Por exemplo, em
rustterá de fazer algo do géneroVec<Box<Node>>. Empythonnão terá qualquer dificuldade.
- Obs. esta recursividade também levanta problemas em algumas linguagens. Por exemplo, em
- Implemente. A função
leaf(value)cria uma folha (isto é, um nó sem filhos). - Implemente. A função
binop(op, lhs, rhs)cria um nó com valueope dois filhos:lhserhs. Considere variantes em quelhs, rhssãoNodeou são um tipo qualquer. - Implemente. A função
node(value, children)aceita um número variável de valores emchildren. Por exemplonode("plus", 3, 4, 5)e nãonode("plus", [3, 4, 5]). - Escrita. A função
repr(node)devolve umastringcom a representação de uma árvore, um valor por linha. Indente os descendentes. Por exemplo:
plus
- 3
- times
- 4
- 5
Alternativamente, as árvores podem ser representadas por listas de listas. Por exemplo:
("plus" 3 ("times" 4 5)) =
("plus"
3
("times"
4
5
))
Desta forma, em geral n = Node(value, children) define a lista [n.value] + CHILDREN em que CHILDREN é a lista das representações dos nós em n.children.
N.B. usando a notação do python, tree.children = tree[1:] e tree.value= tree[0]. Além disso, a representação das folhas é o próprio valor, não uma lista.
Pesquisa:
- Implemente. A função
searchpara pesquisas (em profundidade e em largura).- Começe com pesquisas por valor exato: Por exemplo,
search(tree, value)procura emtreeum nóntal quen.value == value. No caso de existir um nó nessas condições, devolve o caminho para esse nó.
- Começe com pesquisas por valor exato: Por exemplo,
Caminhos para nós descendentes. Por exemplo, se tree for o exemplo acima, o caminho para chegar ao nó com o valor 4 é a lista [1, 0] porque começando na raiz (o nó com valor plus) escolhe-se o filho na posição 1 (o nó com valor times e filhos [4, 5]) e, desse nó escolheu-se o filho na posição 0; Isto é, o caminho [0, 1] indicas os indices dos filhos escolhidos, quando se “desce” a árvore.
O caminho para chegar ao valor 5 seria [1, 1] e para chegar a times seria apenas [1]. Finalmente [0] dá o valor 3 e o caminho [] leva ao valor … (exercício).
-
Implemente. A função
subtree(tree, path)devolve o nó que corresponde ao caminhopath. Se não existe tal nó, devolve “não definido”. -
Generalize. Há várias generalizações interessantes:
- Use um predicado em vez de um valor. Por exemplo, para encontrar um nó com o valor par:
tree.searchD(lamba x: x.value % 2 == 0). - Encontre todas as ocorrências em vez de apenas uma. Ou encontre até
nocorrências. Por exemplo:tree.search(lambda x: len(x.children) > 2, n=42)para encontrar 42 nós com mais do que dois filhos. Convencione que, senfor “não definido” procura todas as ocorrências.- A pesquisa de todas as soluções também tem um tratamento interessante que consiste em implementar a pesquisa como uma stream que produz um novo nó sempre que solicitada. No caso do
pythonpode usaryield. Noutras linguagens, ymmv.
- A pesquisa de todas as soluções também tem um tratamento interessante que consiste em implementar a pesquisa como uma stream que produz um novo nó sempre que solicitada. No caso do
- Implemente outras estratégias de pesquisa. Por exemplo a Iterative deepening depth-first, é uma forma melhorada de pesquisas em profundidade.
- Use um predicado em vez de um valor. Por exemplo, para encontrar um nó com o valor par:
Analisadores LL(1)
- Considere a GIC
$$ \begin{aligned} Expr \to atom \alt (\ Seq\ ) \cr Seq \to \nil \alt Expr\ Seq \cr \end{aligned} $$ em que os terminais são $atom, ($ e $)$.
Verifique (manualmente) se é LL(1) e, nesse caso, implemente um analisador sintático LL(1). A função
parse(s)tem como argumento a stringse devolve uma árvore.
- Comece por separar (tokenize) a palavra numa lista de símbolos.
- Precisa de um “contexto” de processamento com:
- O símbolo seguinte:
next. - A lista dos símbolos que faltam processar.
- A função
consume(symbol).
- O símbolo seguinte:
- Processe a lista de tokens usando as funções
proc_Expr(token, tokens, tree)eproc_Seq(token, tokens, tree):tokené o símbolo de avanço.tokenssão os restantes símbolos da palavras (incluindotoken).treeé a árvore que resulta do processamento da função.
- Vai precisar de funções auxiliares como
consume(token, tokens)
Uma biblioteca para GIC LL(1)
Se resolver sozinho estas alíneas ganha o direito de se gabar nas aulas de ALP durante uma semana. E o dever de ajudar os seus colegas.
- ‡ Implemente. O método
firsts()que devolve um mapa do tiposymbol: set<symbol>que associa a cada símbolo (variável ou terminal) da gramática o conjunto dos seu primeiros.- ‡ Implemente. O método
follow()que devolve um mapa do tiposymbol: set<symbol>que associa a cada símbolo (variável ou terminal) da gramática o conjunto dos seu seguintes.
Análise Sintática LL(1)
- Implemente. O método
firsts_of(symbol)devolve o conjunto dos primeiros desymbol. - Implemente. O método
follow_of(symbol)devolve o conjunto dos seguintes desymbol. - Implemente. O método
directors(rule)devolve o conjunto de diretores da regrarule. - Teste. O método
is_LL1()testa segrammaré LL(1).
Uma biblioteca para GIC LR
Itens
- Represente. Um item LR(1) é representado pela classe
Itemcom atributos:ruleuma regra.lookaheaduma lista de símbolos.positionum inteiro, que indica a posição do “ponto”.
- Teste. O método
is_complete()testa se o item é completo. - Implemente. O método
active_prefix()devolve o prefixo até à posição do “ponto”. - Implemente. O método
active_symbol()devolve o símbolo imediatamente a seguir ao ponto se o item não for completo e “não definido” caso contrário. - Implemente. O método
active_suffix()devolve o sufixo desde a posição a seguir ao “ponto”.- N.B:
active_prefix + active_symbol + active_suffixdeve reconstruir o lado direito da produção.
- N.B:
- Implemente. O método
transition(symbol)devolve o item que resulta de “ler”symbol. Isto é, sesymbol == active_symbolno novo item o “ponto” avança uma posição. Caso contrário devolve “não definido”. - Escrita. O método
__repr__()devolve umastringda formaC〈V → P · A S ⎅ L〉em que:Cé “'★'” quando o item é completo e vazia ('') caso contrário.Vé o lado esquerdo da produção.P,AeSsão o prefixo, símbolo e sufixo ativos.Lé a lista dos símbolos de avanço, separados por espaços. Se for vazia, use∅.- Use mesmo os símbolos indicados: ★〈→·⎅∅〉
Análise Sintática, Autómato dos Itens Válidos
Na biblioteca para os AFD estes são construídos com uma lista de transições, o estado inicial e uma lista de estados finais. Além disso, os estados são inteiros.
Mas, na construção do Autómato dos Itens Válidos os estados “contêm” conjuntos de itens. Esta diferença é resolvida mantendo uma associação (mapa, dicionário) dos estados do AFD para os conjuntos de itens. A vantagem é que não é preciso mudar a implementação dos AFD. A desvantagem é que se torna necessário fazer alguma “manutenção” dessa associação.
-
Representação. Uma classe
VIAcom atributos:grammara gramática.fsao autómato dos itens válidos calculado paragrammar.statesa associação dos estados do autómato para os conjuntos de itens.tablea tabela de análise sintática, uma associação dos estados+avanços do autómato para reduções/transferências.phaseum inteiro (ou enum) para marcar a fase de processamento:INITIAL = 0→GRAMMAR_OK→START_OK→VIA_OK→TABLE_OK. Se algum destes passos correr mal →ERROR.
-
Construção. O método
make_VIA(). Segrammar.is_valid()incrementaphase. -
† Implemente. O método
calc_startCore()que calcula o núcleo do estado inicial devia. Devolve um conjunto de itens. -
† Implemente. O método
close(itens)que calcula o fecho de um conjunto de itens. Devolve um conjunto de itens. -
Implemente. O método
build_START()que calcula o estado inicial devia. Se correr bem incrementaphase.
Se resolver sozinho todas as alíneas seguintes ganha o dever de ajudar os seus colegas. E o direito de se gabar nas aulas de ALP durante uma semana.
- † Implemente. O método
build_FSA()processagrammarpara definir o autómatofsa, a associaçãostateseis_built. Se correr bem incrementaphase. - † Implemente. O método
build_TABLE()processagrammar,fsaestatespara definirtable. Se correr bem incrementaphase.
- † Implemente. O método
derive(word)para encontrar uma derivação dewordpela gramáticavia.grammar. N.B. não é necessário implementar autómatos de pilha. - † Implemente. O método
derivation_tree(word)que calcula a Árvore de Derivação deword. - Controlo. Use
phasepara evitar computações repetidas, precoces ou desnecessárias. Por exemplo, suponha que houve um erro a calcular o estado inicial. Então quando “chama”build_FSAdeve evitar calcular o AFD. Por outro lado, se já calculoufsacom sucesso e “acidentalmente” chamabuild_FSAnão há razão para repetir esses cálculos.- Também pode usar
phasepara implementar cálculosbuild---“inteligentes” (Ah! Ah!). Suponha que “chama”build_TABLEmasphase < VIA_OK. Nesse ponto pode chamarbuild_VIAque por sua vez faz uma análise semelhante.
- Também pode usar
Representação e Processamento de Programas
 |
|---|
Este capítulo inspira-se em grande parte (e copia pontualmente) no artigo (How to Write a (Lisp) Interpreter (in Python)) de Peter Norvig, cuja leitura se recomenda.
Introdução
Procura-se ilustrar uma das principais aplicações da análise sintática: A implementação de linguagens de programação.
Antes de se definir a própria linguagem de programação e considerar os aspetos da implementação do respetivo analisador sintático e do interpretador faz-se uma revisão dos termos e processos envolvidos.
Alguns termos relevantes, alguns já familiares, são:
- Símbolos: “entidades” indivisíveis e distintas entre si. Um conjunto de símbolos é um alfabeto.
- Palavra: sequência finita de símbolos.
- Linguagem: conjunto de palavras.
- Gramática: regras que permitem especificar certas linguagens.
- Representação: descrição da estrutura duma palavra, de acordo com uma gramática.
Também é importante recapitular alguns processos:
- A análise sintática consiste em decidir de uma palavra $p$ está, ou não, numa linguagem $L$: “$p \in L$?”. No caso da linguagem ser gerada por uma certa gramática $G$, isto é, se $L = L(G)$, a questão da análise sintática passa a ser “$S \ider p$?” em que $S$ é o símbolo inicial de $G$.
- Para o processamento de programas, em particular para a interpretação e/ou compilação, não basta saber que $S \ider p$; É mais importante representar a estrutura de $p$ de acordo com as regras de $G$. Essa representação pode ser, por exemplo, a árvore da derivação de $p$ ou a sua própria derivação, isto é a sequência de regras aplicadas passo-a-passo em $S \ider p$.
- A representação do programa é processada pelo interpretador, que mantém uma configuração interna, atualizada conforme a computação avança nas instruções.
- A evolução da computação depende, por um lado, dos tipos das instruções e, por outro, dos valores das expressões.
Representação de Programas e/ou Expressões
É necessária uma estrutura de dados adequada à representação e ao processamento de programas.
Começando pelas expressões algébricas:
| Árvore de Derivação | Árvore Simplificada | Valoração da Expressão |
|---|---|---|
 |  |  |
-
A palavra
2 + (3 * 4)representa a expressão algébrica $2 + (3 \times 4)$ mas, como “simples” sequência de símbolos, perde-se a estrutura da expressão que representa. -
As sequências (isto é, listas) não são adequadas para processar expressões ou programas. Por exemplo, para calcular o valor de $2 + (3 \times 4)$ primeiro avalia-se a parte $3 \times 4$ e depois esse resultado é somado a $2$.
-
A estrutura da expressão algébrica resulta de uma certa gramática, implícita na respetiva definição formal.
-
A linguagem das expressões algébricas resulta, por exemplo, da seguinte GIC:
E → E + T | E - T | T T → T * U | T / U | U U → N | V | ( E )em que
Ndefine números (-1,2.45E-5,42.021, etc) eVvariáveis (a,Largura, etc). -
De acordo com esta GIC a palavra
2 + (3 * 4)tem a Árvore de Derivação acima. -
Na Árvore Simplificada a representação em árvore permite calcular o valor da expressão, propagando os valores das folhas para a raíz e, em cada nó, aplicando a operação adequada conforme o tipo do nó.
-
A implementação de árvores por uma estrutura de dados é assunto doutras disciplinas. Aqui estamos interessados numa representação simples de árvores, de preferência sem a introdução de novos tipos, operações, etc
-
A árvore simplificada fica representada (em
Python) pelo tuplo('+', 2, ('*', 3, 4)). -
Em geral, cada nó tem um conteúdo
Xe descendentesD1, …,Dn. Este nó é representado pelo tuplo(X, D1, ..., Dn)com a convenção de que as folhas(Z)são representadas apenas porZ. -
Subindo a árvore de
2 + (3 * 4)temos:- Folhas
2,3e4(e não(2)por exemplo). - A multiplicação é o tuplo
('*', 3, 4)porque o respetivo conteúdo é'*'(uma stringPython) e tem dois descendentes,3e4. - O nó da soma tem conteúdo ‘+’ e dois descendentes, a folha
2e a sub-árvore('*', 3, 4). Fica representado por('+', 2, ('*', 3, 4)).
- Folhas
Esta forma de representar as (estruturas das) expressões vai ser aplicada à representação (das estruturas) dos programas.
Também o exemplo do cálculo do valor da expressão algébrica orienta a implementação do interpretador.
Desenho de uma Linguagem de Programação
Como já está esboçado um esquema geral para representar programas, agora pode-se tratar da linguagem propriamente dita.
O que se pretende e/ou necessita numa linguagem de programação?
Em geral, numa linguagem de programação encontra-se:
- Expressões e Variáveis.
- Instruções e Sequências.
- Condicionais.
- Ciclos.
- Funções.
- Entrada/Saída.
Mais especificamente,
- Expressões e Variáveis. As expressões definem os valores que os programas processam e as variáveis “mantêm” esses valores para uso posterior.
Por exemplo, a instrução
a = 2 + (3 * 4)emPythondefine um certo valor que fica guardado na variávelae que pode ser usado posteriormente, como ema % 2 == 0.
- Instruções e Sequências. Um programa é uma sequência (ou bloco) de instruções. “Correr” um programa significar avançar uma instrução de cada vez ao longo dessa sequência.
São comuns certas convenções sobre as sequências que “efetivamente” definem um programa. Por exemplo, em
Co programa é o bloco de instruções que está na funçãomaine tudo o resto é “auxiliar”.
- Condicionais. Um condicional permite certas condições ativarem e desativarem blocos de instruções.
A sintaxe mais comum dos condicionais é
if (C) A else Bcom pequenas variantes conforme a linguagem.
- Ciclos. Um ciclo repete um certo bloco de instruções em função de uma condição.
Quando o número de repetições é conhecido de antemão é comum usar-se a sintaxe
for(i = 0; i < n; i++) Apara repetirnvezes as instruções deA.Quando as repetições estão dependentes de uma condição, a forma
while (C) A, que testaCe repeteAenquanto a condiçãoCfor verdadeira, é comum.Também se usa a forma
do A while (C), que correApelo menos uma vez, antes de testarC.
- Funções. As funções são uma forma simples de evitar repetição de código e de acrescentar instruções “novas” a uma linguagem de programação.
Se for necessário calcular
2 + 2,2 + 3,2 + 4, …,2 + 42não se escrevem 40 instruções quase iguais. Define-se uma função que mantém a parte comum do código repetido e usa variáveis locais para os valores que variam. Sendo possível, a função pode ser evocada num ciclo.
Funções Anónimas. Formalmente, uma função não precisa de ter um nome. Nalgumas linguagens mais arcaicas, como o
C, as funções anónimas (ou lambdas) não são suportadas diretamente. Com a maior disponibilidade do processamento de coleções têm ganho popularidade. Por exemplo, emJavafoi introduzido o operador->, oJavascripte oC#têm o=>, noPythonusam-se expressõeslambdae noRusta sintaxe é|var| instr, etc. TL/DR: As funções anónimas são fixes.
- Entrada/Saída. Um programa, enquanto processador de informação precisa de canais de entrada e de saída de dados.
As formas mais simples de entrada e saída de dados pressupõem uma consola onde o utilizador digita e lê os dados que, respetivamente, dão entrada no, ou são escritos pelo, programa.
Lisp
O Lisp é uma das mais antigas, influentes e avançadas linguagens de programação.
Além disso, all the programming languages converge to Lisp e any sufficiently complicated program contains an ad hoc, informally-specified, bug-ridden, slow implementation of half of Common Lisp.
Aspeto de um programa Lisp (especificamente, Common Lisp):
(defun fib (x)
(if (< x 2)
1
(+ (fib (- x 1)) (fib (- x 2)))
)
)
(fib 6) ; resultado: 13
A “excecionalidade” do Lisp está nas possibilidades que resultam da sua simplicidade. “Elegant weapons” significa que certas ideias muito simples são extremamente efetivas.
Por exemplo, (+ 41 1) é uma lista com três elementos, uma expressão que vale 42 e
uma (instrução de) evocação da função +.
-
Lispsignifica LISt Processor. Além dos tipos básicos (inteiros, doubles, strings) tem listas. Ao contrário dosarrayem muitas linguagens, uma lista doLisppode ter elementos de tipos diferentes. Por exemplo,(42 3.14 "fourty-two" ("sub" lista)). -
No
Lispas instruções também são expressões. Isto é,(+ 2 (* 3 4))é simultaneamente uma expressão (com valor 12) e uma instrução (neste caso, evocar a função"+").- Por exemplo, um condicional é
(if C A B)e, comoC,AeBsão expressões, o valor do condicional é o valor do ramo que foi seguido.
- Por exemplo, um condicional é
-
A sintaxe segue fielmente a representação das árvores feita acima (as vírgulas são descartadas). Isto é: Um programa
Lispé a sua própria representação! É possível um programaLispler, analisar e modificar o seu próprio código enquanto corre. Em particular, oLispé homoicónico.
No resto deste capítulo define-se uma linguagem de programação,
ALisP, inspirada noLisp. Além das propriedades acima, acresce ainda que a gramática para a sintaxe é extremamente simples e LL(1), o que permite implementar (quase) diretamente um analisador sintático.
Semântica Informal da ALisP
Uma antevisão da
ALisP.
-
Variáveis e Expressões:
(set a (+ 30 12))define a variávelae dá-lhe o valor42. A expressão completa também fica com esse valor. -
Instruções e Sequências:
(seq (set a (+ 40 10)) (set a (- a 8)))executa as duas instruções. Fica com o mesmo valor que a última sub-expressão. -
Condicionais:
(if (== a 42) CERTO (> 0 1))calcula o valor de(== a 42); Se forTruecalcula e fica com o mesmo valor queCERTO; Caso contrário calcula(> 0 1)e fica com esse valor. -
Ciclos:
(while (< a 42) (set a (+ a 1)))repete o “passo”(set a (+ a 1))enquanto a condição(< a 42)for verdadeira. Quando (se) termina fica com o valor do “passo”. -
Funções (anónimas):
(fn (x) (== x 42))define uma função anónima com argumentosxe “corpo”(== x 42). A variávelxestá limitada ao “corpo” da função. Devolve o valor do “corpo” quandoxtem o valor com que a função é evocada. Por exemplo, em(seq (set dobro (fn (x) (* 2 x) )) (dobro 21) )a evocação
(dobro 21)define o valor dexcomo21e, portanto, a função devolve (surpresa!)42. -
Entrada/Saída:
(read)é uma forma especial. Tem o valor que o utilizador escrever na consola;(write 42)esteve42na consola. Tem o valor da expressão que é escrita.
Um programa ALisP simples, que pergunta o nome do utilizador e o cumprimenta:
(seq
(write (What is your name?))
(set name (read))
(Hello name .)
)
Um defeito semântico da atual versão da
ALisPé que os símbolos, como emWhat is your name?são tratados comostring, o que simplifica a implementação mas torna o código mais imprevisível. Por exemplo, o valor de(Hello name .)varia conformenameé, ou não, uma variável e esse facto não pode ser deduzido olhando apenas para esta expressão.
Analisador Sintático com Representação
Embora a função principal da análise sintática seja determinar se
p ∈ L(G), aqui pretende-se ir além dessa resposta e obter a representação depem termos da sua árvore (simplificada) de derivação na gramáticaG.
Gramática ALisP
Em termos de sintaxe a linguagem é a linguagem dos parêntesis equilibrados, com átomos, definida pela seguinte gramática, que designamos ALisP:
Expr -> atom | ( Seq )
Seq -> λ | Expr Seq
onde atom representa um terminal átomo isto é, uma “palavra contígua”: uma string não vazia sem espaços nem parêntesis.
Os átomos podem (devem!) ser representados pela sua própria sub-gramática. Para o efeito pretendido (análise sintática com representação) esse exercício iria apenas acrescentar ruído. Em vez disso, é implementado o teste
is_atom(x), posteriormente usado pelo analisador sintático.
Para implementar o analisador sintático LL(1) é preciso calcular os diretores de cada produção.
Geradores de λ
| Λ |
|---|
Seq |
Primeiros e Seguintes
| Variável | Primeiros | Seguintes |
|---|---|---|
Expr | atom, ( | atom, (, ) |
Seq | atom, ( | ) |
Diretores
| Produção | Diretores |
|---|---|
Expr -> atom | atom |
Expr -> ( Seq ) | ( |
Seq -> λ | ) |
Seq -> Expr Seq | atom, ( |
A tabela dos Diretores indica que a gramática
ALisPé LL(1), pelo que pode ser aplicado o método dado no respetivo capítulo para construir um analisador sintático. Porém, também se pretende obter a representação da (árvore simplificada da derivação da) palavra.
Representação de Árvores
Como já foi tratado acima, qualquer árvore pode ser representada em Python por tuple aninhados. Mais especificamente:
Representação de nós em
Python. O nó com com conteúdoxe descendentesd1, …,dn, em quexe osdisão valoresPython, é representado pelotuple(x, d1, ..., dn)Por convenção a representação das folhas não usa parêntesis. Em vez de
(x)usa-se apenasx.
Por exemplo, a árvore de 2 + (3 * 4) é representada por
('+', 2, ('*', 3, 4))
Analisador Sintático com Representação
O analisador sintático com representação é implementado a partir da base definida no capítulo sobre a análise sintática LL(1). Acrescenta-se uma forma de se obter a representação em árvore e de tratar da especificidade dos átomos.
Para a implementação do analisador sintático compensa considerar com algum detalhe o contexto em que a análise LL(1) decorre. Em particular, importa tratar rigorosamente o processamento do avanço, de consumir e dos erros.
Contexto LL(1) Especificamente, uma instância
cda classeContextLL1:
- É construída com a palavra a ser analisada.
c.next()devolve o próximo símbolo da palavra, se existir; caso contrário devolveNone.c.consume(x)consome o próximo símbolo se o valor deste forx; caso contrário levanta uma exceção.c.error(m)levanta uma exceção com a mensagemm.- Adicionalmente,
c.is_complete()testa se não existe seguinte.
class ContextLL1:
"""Tracks and supports the state of a LL1 parsing process."""
def __init__(self, word):
self.word = word
self.pos = 0
def is_complete(self):
"""Checks if the parsing process is complete."""
return self.pos >= len(self.word)
def next(self):
"""Returns the next (unread) token."""
if not self.is_complete():
return self.word[self.pos]
else:
return None
def consume(self, symbol):
"""'Consumes' symbol, advancing if possible."""
if not self.is_complete() and self.next() == symbol:
self.pos += 1
else:
self.error(f"** ERROR ** Can't CONSUME '{symbol}' while expecting '{self.next()}'.")
def error(self, message):
"""Error handling."""
raise Exception(f"{message}\nWord: {self.word}\nRead: {self.word[self.pos:]}\nUnread: {self.word[:self.pos]}")
def __repr__(self):
"""String representation."""
return f"\"{' '.join(self.word[:self.pos])}\" | \"{' '.join(self.word[self.pos:])}\""
Suporte. São necessárias algumas funções de suporte. Em particular
tokenize(text)aceita umastringe devolve a lista das sub-palavras separadas por espaços, com tratamento especial dos parêntesis.is_atom(symbol)testa sesymbolé um átomo: umastringnão vazia e sem ocorrências de espaços ou parêntesis.atom_value(atom)devolve o “valor” do átomoatom, conformeatompode ser convertido numìntsenão numfloatsenão no próprioatom.
def tokenize(text):
"""
Converts a string to a list of tokens.
"""
text = ''.join(ch for ch in text if ch.isprintable())
text = text.replace("(", " ( ").replace(")", " ) ")
tokens = text.split(" ")
tokens = [tok.strip() for tok in tokens]
tokens = [tok for tok in tokens if len(tok) > 0]
return tokens
def is_atom(symbol):
"""
Tests if a symbol is an atom.
"""
return isinstance(symbol, str) and \
len(symbol) > 0 and \
(not ' ' in symbol) and \
(not '(' in symbol) and \
(not ')' in symbol)
def atom_value(atom):
"""
Gets the value of an atom. BAD BAD NOT GOOD CODE.
"""
value = None
try:
value = float(atom)
(d, i) = math.modf(value)
value = int(i) if d == 0 else value
except:
value = atom
return value
- A implementação do analisador sintático, segundo o processo LL(1), consiste em definir uma função para cada variável da gramática
ALisPe, em cada uma dessas funções, usar o avanço e os diretores para “percorrer” a regra adequada. - A implementação LL(1) base é aumentada de forma se obter uma representação parcial em cada função associada.
- Todo o processo da análise sintática com representação é concretizado em
parse(text). Esta função aceita como argumentotext, umastring, e, se corresponder a uma palavra gerada pela gramática, devolve a respetiva representação em árvore.
#
# Rule | Dir
# ----------------|-------
# Expr -> ( Seq ) | (
# Expr -> atom | atom
#
def proc_Expr(context):
next_symbol = context.next()
if next_symbol == "(":
context.consume("(")
seq = proc_Seq(context)
context.consume(")")
return seq
elif is_atom(next_symbol):
context.consume(next_symbol)
return atom_value(next_symbol)
else:
context.error(f"** ERROR ** Can't use Expr with next '{next_symbol}'.")
#
# Rule | Dir
# ----------------|-------
# Seq -> Expr Seq | atom (
# Seq -> nil | )
#
def proc_Seq(context):
next_symbol = context.next()
if is_atom(next_symbol) or next_symbol == "(":
e = proc_Expr(context)
s = proc_Seq(context)
return (e,) + s
elif next_symbol == ")":
return tuple()
else:
context.error(f"** ERROR ** Can't use Seq with next '{next_symbol}'.")
def parse(text):
word = tokenize(text)
if all(is_atom(x) or x in "()" for x in word):
context = ContextLL1(word)
expr = proc_Expr(context)
return expr
else:
return None
A implementação do processo de análise sintática chega ao fim da aplicação dos capítulos anteriores.
Recapitulando o que foi feito até aqui:
- Definiu-se uma gramática para especificar a sintaxe da
ALisP.- Essa gramática é LL(1) e implementou-se um analisador sintático que devolve uma representação em árvore da palavra dada.
Se tivesse sido escolhida uma linguagem com sintaxe mais complexa poderia ser necessário um analisador LR(1). Porém, o objetivo aqui é ir além da matéria anterior, implementando um interpretador da
ALisP.
Interpretador
A análise sintática (da ALisP) fica isolada na função parse(text), que devolve uma árvore com a estrutura de text de acordo com a gramática ALisP. Por exemplo, parse("(+ 2 (* 3 4))") devolve ('+', 2, ('*', 3, 4)).
O passo seguinte consistem em associar um valor (a semântica) a cada representação (à sintaxe), de forma a construir a ALisP com as caraterísticas pretendidas. Nomeadamente, pretende-se que a ALisP tenha:
- Expressões e Variáveis.
- Instruções e Sequências.
- Condicionais.
- Ciclos.
- Funções.
- Entrada/Saída.
além de, é claro, certas funções base.
Para correr da forma esperada, um programa precisa de um certo “contexto” onde é mantida e atualizada informação sobre as variáveis. Por exemplo, no programa
(
(set a 42)
(set b (- a 2))
(write (b a))
)
na primeira instrução é criada uma variável com nome a e valor 42 e na segunda instrução o valor de a é consultado, operado e o resultado define o valor da recém-criada variável b. Por fim, tanto o valor de b como de a são consultados para definir a lista (b a) que será escrita na consola.
Funções Base
As funções base definem cálculos “diretos” que dependem apenas dos valores dos argumentos e não afetam o contexto do programa.
Entre as funções base estão incluidas as operações aritméticas +, -, * e /; as relações de ordem <, >, <= e >=; de igualdade == e !=; as operações booleanas and, or e not; as funções trigonométricas sin e asin; e as funções para decompor listas head, tail e nth. A escolha das funções básicas deve corresponder às necessidades que levam ao desenvolvimento da linguagem de programação. Por exemplo, o octave é uma linguagem de manipulação de matrizes numéricas e tem pré-definidas as respetivas operações.
No âmbito da ALisP é suficiente definir as funções base como um dicionário Python onde o nome da função está associado a um tuple com a aridade e uma expressão lambda (isto é, a versão Python das funções anónimas):
import math
BASE_FUNCTIONS = {
#
# Aritméticas
#
'+': (2, lambda x, y: x + y),
'-': (2, lambda x, y: x - y),
'*': (2, lambda x, y: x * y),
'/': (2, lambda x, y: x / y),
#
# Ordem
#
'>': (2, lambda x, y: x > y),
'>=': (2, lambda x, y: x >= y),
'<': (2, lambda x, y: x < y),
'<=': (2, lambda x, y: x <= y),
#
# Igualdade
#
'==': (2, lambda x, y: x == y),
'!=': (2, lambda x, y: x != y),
#
# Booleanas
#
'not': (1, lambda x: not x),
'and': (2, lambda x, y: x and y),
'or': (2, lambda x, y: x or y),
#
# Trigonométricas
#
'sin': (1, lambda x: math.sin(x)),
'asin': (1, lambda x: math.asin(x)),
#
# Listas
#
'head': (1, lambda x: x[0]),
'tail': (1, lambda x: x[1:]),
'nth': (2, lambda n, x: x[n]),
}
Esta representação das funções base pode ser facilmente modificada de forma a proporcionar, à partida, instruções adequadas ao domínio que se pretende trabalhar. Por exemplo, para computação gráfica 2D as funções base podem incluir os controlos de uma “tartaruga”, forward, turn, up, down e set_color.
Contexto
O contexto é, essencialmente, um dicionário que associa o nome de cada variável ao respetivo valor. Além disso, é necessário considerar que as funções definem variáveis locais mas também têm acesso às variáveis externas.
Em
(seq
(set x 21)
(set dobro (fn (x)
(* x 2)
))
(set x (- x 1))
(x (dobro 10))
)
a variável x é local e externa em dobro. Na última linha, (x (dobro 10)), tem o valor 20 no primeiro elemento e, quando a função dobro é evocada, é usado o valor local, 10, passado como argumento. O papel da instrução seq é esclarecido mais tarde.
A implementação do contexto é:
class ALisPContext:
def __init__(self, outer):
self.outer = outer
self.local = dict()
def defines(self, key):
return key in self.local.keys() or key in self.outer.keys()
def set(self, var_name, var_value):
self.local[var_name] = var_value
def keys(self):
return self.local.keys() | self.outer.keys()
def __getitem__(self, key):
return self.value(key)
def value(self, name):
result = None
#
if name in self.local.keys():
result = self.local[name]
elif name in self.outer.keys():
result = self.outer[name]
elif name == 'True':
return True
elif name == 'False':
return False
elif is_atomic(name): # 42, -4.2, ola
result = atom_value(name)
#
return result
ALisPContextUma instânciacdeALisPContext:
É construída em relação a um contexto “externo” (que pode ser o dicionário vazio,
{}).
c.set(var_name, var_value)define uma associação da variávelvar_nameao valorvar_value.
c.defines(key)testa se o nomekeytem uma associação, local ou externa.
c.keys()devolve o conjunto das chaves, locais ou externas, conhecidas.
c[atom]ouc.value(atom)devolve, por ordem:
- O valor associado a
namese existe essa associação a) local ou b) no contexto externo.- Se
nameé"True"ou"False"os valores booleanos correspondentes.- Se
nameé atómico (de acordo comis_atom) o respetivo valor calculado poratom_value.None.
O método interessante de ALisPContext é value que, além de obter os valores associados a uma variável local ou externa, ainda proporciona os valores dos átomos e das constantes booleanas.
Valoração
A valoração consiste em calcular o valor de uma representação, isto é, definir uma semântica da (representação) sintaxe.
Esse cálculo depende de um contexto, que mantém e atualiza os valores das variáveis.
Por exemplo, A palavra 2 + (3 * 4) tem representação ('+', 2, ('*', 3, 4)), obtida pelo analisador sintático. A esta representação corresponde o valor 14, que resulta de aplicar as respetivas operações aritméticas em cada nó, a começar pelas folhas.
Resumidamente, 14 é a semântica da sintaxe 2 + (3 * 4) e é calculada usando a representação intermédia ('+', 2, ('*', 3, 4)).
Em cada nó o conteúdo (daqui em diante representado por op) define a operação e os descendentes vão definir os valores dos argumentos (daqui em diante, args) dessa operação:
eval(('+', 2, ('*', 3, 4))) =
soma(eval(2), eval(('*', 3, 4))) =
soma(2, mult(eval(3), eval(4))) =
soma(2, mult(3, 4)) =
soma(2, 12) =
14
A valoração é uma função recursiva que, em cada nó
(op, *args), calcula o valor dos argumentos*argse, depois, conforme o valor deop, combina esses valores no resultado correspondente.Porém, um programa a correr define e consulta variáveis, escolhe ramos num condicional, etc.
O cálculo da valoração depende do contexto e das funções base. Um esquema incompleto da implementação segundo esses pressupostos será, por exemplo:
def eval(expr, context=None, ops=BASE_FUNCTIONS):
if context is None:
context = ALisPContext({})
#
# expr is ATOM
#
context_value = context.value(expr)
if context_value is not None:
return context_value
#
# expr is LIST
#
elif is_list(expr) and expr != NIL:
#
# expr = (op args...)
#
op = head(expr)
args = tail(expr)
#
# Use op and len(args) to do the right step
#
if op in ops.keys():
# BASE FUNCTIONS
elif op == 'write' and len(args) == 1:
# WRITE: (write MESSAGE)
elif op == 'read' and len(args) == 0:
# READ: (read)
elif op == 'fn' and len(args) == 2:
# FUNCTIONS: (fn ARGS INSTR)
elif op == 'set' and len(args) == 2:
# DEFINE/UPDATE VARIABLES: (set VAR VALUE)
elif op == 'while' and len(args) == 2:
# CYCLES: (while GUARD INSTR)
elif op == 'if' and len(args) == 3:
# CONDITIONALS: (if COND TRUE_INSTR FALSE_INSTR)
elif op == 'seq':
# SEQUENCE OF INSTRUCTIONS (LAST VALUE)
# (seq *INSTR)
elif is_list(op):
# DEFER: (OP *ARGS)
elif context.defines(op):
# CONSULT VARIABLE: VAR
else:
# FALLBACK: (TERMINAL *REST)
#
# expr is ALIEN... maybe raise error?
#
else:
return expr
Funções Base
As funções base proporcionam alguma funcionalidade inicial e também uma ponte à linguagem hospedeira, o
Pythonneste caso.
Para calcular o valor de uma função base como, por exemplo, (+ 2 3), fica op == "+", args == (2, 3) e os passos são:
- Verificar se
op(neste caso,+) é uma chave no dicionário das funções base (ops). - Validar a aridade (
if len(args) >= arity). - Chamar recursivamente
evalnos argumentos:val_args = tuple(eval(x, context, ops) for x in args[:arity]). - Devolver o valor da função associada a
opquando aplicada aos valores dos argumentos:return func(*val_args).
#
# BASE FUNCTIONS
#
if op in ops.keys():
arity, func = ops[op]
if len(args) >= arity:
val_args = tuple(eval(x, context, ops) for x in args[:arity])
return func(*val_args)
else:
return None
Entrada/Saída
As funções de entrada e saída permitem interações com o utilizador via uma consola.
A sintaxe é:
(write MESSAGE)em queMESSAGEé um valor qualquer a ser escrito na consola.(read)para ler um valor da consola.
- A “real” interação ocorre via as funções correspondentes no
Python:printparawriteeinputpararead. - No caso da saída (
write):- É admitido exatamente um argumento.
- Recursivamente, é calculado o valor desse argumento.
- O valor, que é um
tuple, é enviado para a consola (print) numa sintaxe compatível comALisP(expr_repr).
- Para a entrada (
read):- Não são admitidos argumentos.
- É lido o texto da consola via
input. - Esse texto é analisado (
parse). - Recursivamente, é calculado o valor da representação obtida na análise anterior.
#
# WRITE
#
elif op == 'write' and len(args) == 1:
value = eval(args[0], context, ops)
print(expr_repr(value))
return value
#
# READ
#
elif op == 'read' and len(args) == 0:
user_input = input()
user_prog = parse(user_input)
value = eval(user_prog, context, ops)
return value
Funções
As funções, em
ALisPsão valores como as listas, números ou textos.A sintaxe é
(fn ARGS INSTR)em quefné a instrução,ARGSé uma lista de variáveis eINSTRé uma lista de instruções.Depois de criada uma função pode ser guardada numa variável para uso posterior.
Por exemplo:
(
(set succ (fn (x) (+ x 1)))
(succ 41)
(succ 0)
)
As funções são o único caso em que eval não é recursiva. No exemplo acima:
- Em
(fn (x) (+ x 1))é definido um certo valor. - No interpretador esse valor é uma instância da classe
Lambda. - Essa instância é construída com os argumentos
(x,)e('+', 'x', 1)que são as representações de"(x)"e"(+ x 1)"respetivamente. - O valor do passo anterior é guardado na variável
succ. - Mais tarde, na linha seguinte,
(succ 41):- É criado um contexto local, onde
xfica com o valor41. - Nesse contexto é calculado o valor de
(+ x 1), usandoeval.
- É criado um contexto local, onde
- Na linha
(succ 0)estes passos são repetidos, mas num novo contexto local em quextem valor0.
A criação do valor Lambda ocorre nas seguintes linhas:
#
# FUNCTIONS
#
elif op == 'fn' and len(args) == 2:
fn_args = args[0]
fn_expr = args[1]
return Lambda(fn_args, fn_expr)
O cálculo das evocações é tratado mais tarde, com as variáveis.
Copiar
Um valor é copiado para uma variável que fica registada no contexto atual. Mais tarde esse valor pode ser recuperado como o valor da variável.
A sintaxe é
(set VAR VALUE)em queVARé um identificador eVALUEuma qualquer expressãoALisP.
- Por exemplo, o seguinte programa tem valor
42:
(seq
(set bad-answer 20)
(set almost-good-answer (* 2 bad-answer))
(+ almost-good-answer 2)
)
No lado do interpretador as instruções set atualizam o contexto da seguinte forma:
#
# DEFINE/UPDATE VARIABLES
#
elif op == 'set' and len(args) == 2:
var_name = uq(args[0]) # Inelegant "dequotation" :(
var_value = eval(args[1], context, ops)
context.set(var_name, var_value)
return var_value
Ciclos
Um ciclo repete um bloco de instruções enquanto uma certa condição é verdadeira.
A sintaxe é
(while GUARD INSTR)em queGUARDé uma condição eINSTRum bloco de instruções.
- Note bem que a
ALisPtem valores booleanosTrueeFalsemas a condição pode ser qualquer valor. Os valores que também valem comoFalsesão0,0.0e(). Todos os restantes valores valem comoTrue. - Por exemplo, o ciclo seguinte escreve a “tabela” dos quadrados de 0 a 10:
(
(set i 0)
(while (<= i 10) (
(write (i (* i i)))
(set i (+ i 1))
))
)
A implementação dos ciclos ALisP usa os ciclos do Python:
#
# CYCLES
#
elif op == 'while' and len(args) == 2:
guard = args[0]
statements = args[1]
last = NIL
while eval(guard, context, ops):
last = eval(statements, context, ops)
return last
Condicionais
Um condicional corre um certo bloco de instruções, ou outro, conforme uma condição é verdadeira ou falsa.
A sintaxe é
(if COND TRUE_INSTR FALSE_INSTR)em queCONDé uma condição eTRUE_INSTReFALSE_INSTRsão blocos de instruções.
- Note bem que a sintaxe “força” três argumentos.
- Por exemplo, o valor de
(seq (set a 10) (if (> a 0) positivo negativo))épositivo.
Tal como nos ciclos, os condicionais do ALisP usam os do Python:
#
# CONDITIONALS
#
elif op == 'if' and len(args) == 3:
cond, seq_true, seq_false = args
if eval(cond, context, ops):
return eval(seq_true, context, ops)
else:
return eval(seq_false, context, ops)
Com esta implementação apenas é percorrido, e calculado o valor do bloco que corresponde ao valor da condição.
Sequências
Uma sequência de instruções corre cada uma, por ordem, e devolve o valor da última instrução. A sequência vazia,
(seq)vale a lista vazia,(), designada NIL.A sintaxe é
(seq *INSTR)em que*INSTRé uma sequência de instruções.
- Note bem que
*INSTRnão é uma lista, mas os seus elementos. - Por exemplo:
- O valor de
(seq 0 1 2 3)é3. - O valor de
(seq (0 1 2 3))é(0 1 2 3). - O valor de
(seq (set a 40) (+ a 2))é42.
- O valor de
A implementação do valor para as sequências é:
#
# SEQUENCE OF INSTRUCTIONS (RETURNS ONLY THE LAST VALUE)
#
elif op == 'seq':
if len(args) == 0:
return NIL
else:
seq = eval(args, context, ops)
return seq[-1]
Diferimento
Na
ALisPo primeiro elemento de uma lista determina como é calculado o valor dessa lista. Pode-se evocar uma função, executar uma instrução ou apenas definir a lista dos valores.Quando o primeiro elemento é também uma lista é preciso começar por determinar o seu valor para seguir no cálculo do valor da lista parente.
Isto é, cálculo do valor da lista parente é diferido pelo valor da lista que é o primeiro elemento.
Por exemplo, o valor de:
(1 2 3)é(1 2 3).(+ 2 3)é5.(if True 42 24)é42.((1 2 3) 2 3)é((1 2 3) 2 3).((if True + *) 2 3)é5.((if False + *) 2 3)é6.
Nos três últimos exemplos, 4., 5. e 6., o primeiro elemento da lista é uma lista que vai definir o modo de calcular o valor da lista parente.
No caso
((1 2 3) 2 3)o valor do primeiro elemento é(1 2 3)que não é nem uma função nem uma instrução. Tal como no exemplo 1., a lista parente tem apenas valores.Nos exemplos 5. e 6. o valor do primeiro elemento é, respetivamente,
+e*. Portanto, o valor da lista parente vai ser diferido, respetivamente, para(+ 2 3)e(* 2 3).
A implementação do cálculo diferido é:
#
# LIST OF INSTRUCTIONS (RETURNS ALL THE VALUES)
#
elif is_list(op):
op_val = eval(op, context, ops)
args_vals = tuple([eval(xi, context, ops) for xi in args])
expr2 = (op_val,) + args_vals
if op_val == op:
return expr2
else:
return eval(expr2, context, ops)
O teste if op_val == op deteta se o cálculo (não) vai ser diferido.
Variáveis e Evocação de Funções
Uma variável pode referir qualquer valor
ALisP, guardado no contexto atual.Quando esse valor é um tipo básico, inteiro,
double, lista,stringou booleano, basta consultar o respetivo valor, guardado no contexto.Quando a variável refere uma função é preciso calcular o valor da função com os argumentos dados.
Por exemplo, o valor de:
(seq (set a 2) (+ a 40)é42.(seq ((set a +)) (a 2 40)é42. O duplo((set a +))é um hack para isolar o valor de(set a +), que é+, uma operação.(seq (set a (fn (x y) (+ x y))) (a 2 40))é42. Esse valor resulta de aplicar a função(fn (x y) (+ x y))aos argumentos(2 40). O corpo e os argumentos desta função forma guardados no contexto, com nomea.
A implementação:
#
# CONSULT VARIABLE
#
elif context.defines(op):
val = eval(op, context, ops)
#
# Function evocation
#
if isinstance(val, Lambda):
arity = len(val.args)
if arity <= len(args):
local_context = AlispContext(context)
for i in range(arity):
local_context.set(
val.args[i],
eval(args[i], context, ops))
return eval(val.expr, local_context, ops)
else:
return None
#
# Other types (number, text, list...)
#
else:
expr2 = (val, ) + args
return eval(expr2, context, ops)
Fallback
Se a “operação” não é um dos casos anteriores deve ser um terminal.
Por exemplo, (4 (+ 1 1)). Neste caso o resultado será (4 2).
A implementação:
#
# FALLBACK
#
else:
return (op,) + eval(args, context, ops)
Exemplos
Funções Recursivas
O seguinte código ALisP define uma pequena biblioteca de funções que ilustram
cálculos recursivos.
(
(set fib (fn (x)
(if (<= x 1)
1
(+
(fib (- x 1))
(fib (- x 2)) )
)
))
(set fact (fn (n)
(if (<= n 1)
1
(*
n
(fact (- n 1))
)
)
))
)
Guarde este código em, por exemplo, recursivas.lisp e experimente:
alisp.py -l recursivas.lisp -e "(fact 100)"e deve obter imediatamente o resultado, que é um número com 246 dígitos ;)alisp.py -l recursivas.lisp -e "(fib 20)"demora um tempo considerável (alguns segundos) e o resultado é10946.- Exercício. A implementação de
fibé muito pouco eficiente (porque o mesmo cálculo é feito duas vezes em cada passo!). Modifique-a (substituindo a recursão por um ciclo) de forma a ter um desempenho melhor. Deve conseguir calcular rapidamente(fib 10000), que tem 2090 dígitos. Jáfib 100000)demora alguns segundos e é um número com 20899 dígitos :D
Adivinhar o Número
O jogo Adivinha o número é um problema simples que permite testar várias caraterísticas de uma linguagem de programação.
- O programa define um número secreto, entre 0 e 100 e o jogador tem de adivinhar esse segredo.
- O programa pede um palpite ao jogador.
- Se a resposta do jogador está certa, o jogo termina. O programa dá os parabéns e diz quantas tentativas foram necessárias.
- Caso contrário, o programa responde
maioroumenorconforme o segredo é maior ou menor que o palpite e volta a pedir um palpite.
Uma implementação do Adivinha o Número em ALisP:
(seq
(set greet (fn (name)
(Hello name . Welcome to the Guess-the-Number game.)
))
(set ord (fn (n)
(if (== 1 n)
first
(if (== 2 n)
second
(if (== 3 n)
third
(n -th)
)
)
)
))
(set main (fn ()
(write (What is your name?))
(set name (read))
(write (greet name))
(set my-secret 42)
(set answer 50)
(set count 0)
(while (!= answer my-secret) (
(set count (+ count 1))
(write (Guess the secret number [(ord count) tentative]))
(set answer (read))
(write
(if (== answer my-secret)
(Very well name . You found that the secret is ** my-secret ** using only count guesses.)
(Not yet, name . The secret is **
(if (< my-secret answer)
smaller
greater
)
** than answer . Try again.
)
)
)
))
))
(main)
BYE
)
Conclusão
Definiu-se uma linguagem de programação, a
ALisP, com sintaxe e a semântica largamente inspiradas/copiadas doLisp, e implementou-se um interpretador:
- A sintaxe é definida por uma gramática LL(1).
- O processo da análise sintática produz uma representação intermédia do programa.
- A
ALisPtem valores inteiros, double, string, booleanos, listas e funções anónimas.- Os valores podem ser guardados em variáveis e consultados posteriormente.
- As instruções proporcionam ciclos e condicionais.
- A interação com o utilizador é feita através da consola.
- O interpretador pode ser inicializado com um conjunto de funções base adequadas a tarefas específicas de um determinado domínio.
Além da interpretação de expressões/instruções/programas são convenientes algumas utilidades, proporcionadas pelo programa alisp.py:
- Uma forma de calcular diretamente o valor de uma expressão:
alisp.py -e "(+ 40 2)". - Uma forma de correr um programa definido num ficheiro:
alisp.py -l guess-the-number.lisp. - Uma forma de usar interativamente a linguagem:
alisp.py --repl. - Estas formas pode ser combinadas, de forma a que, por exemplo, uma biblioteca de funções possa ser carregada para calcular uma expressão e/ou usada numa sessão interativa:
alisp.py -l functions.list -e "(set answer (dobro 21))" --repl
Exercícios
Exercício 01
Para cada um dos pares palavra/gramática seguintes, obtenha a estrutura simplificada da palavra na forma de uma árvore apenas com terminais nos nós.
- Emparelhe
E → E + T | E - T | T ; T → T × F | T ÷ F | F ; F → N | ( E ), em queNrepresenta qualquer número inteiro, com:2,(2),2 + 3,2 × 3,(2 + 3).2 + (3 × 4),2 + 3 × 4e(2 + 3) × 4.2 + (3 + 4),2 + 3 + 4e(2 + 3) + 4.(2 + 3) × (3 + 4),2 + (3 × 3) + 4,2 + 3 × 3 + 4.(2 × 3) + (3 × 4),2 × (3 + 3) × 4,2 × 3 + 3 × 4.
- sequências; lisp;
Exercício 02
Os nós de árvores podem ser representadas por listas heterogéneas (suportadas diretamente, por exemplo, em Python) em que o primeiro elemento é o conteúdo do nó e os seguintes elementos são os descendentes. Por convenção, as folhas representam-se apenas pelo conteúdo (isto é, pelo valor 42 em vez da lista [42]). Implemente:
degree(a)o número de descendentes dea.size(a)o número de nós ema.tree_degree(a)o maior grau dos nós ema.is_leaf(a)seanão tem descendentes.is_inner(a)seatem descendente.is_parent(a, b)seaé ascendente direto deb.is_neighbor(a, b)seaé ascendente direto debou vice-versa.is_antecessor(a, b)seaé ascendente (direto, ou não) deb.is_descendant(a, b)seaé descendente (direto, ou não) dea.level(a, b): sebdescende dea, o número de arestas do caminho que ligaaab; caso contrário,None.width(a, n)o número de descendentes deano níveln.breadth(a)o número de folhas dea.- pesquisas; inserir; remover; podar; menor ascendente comum de dois nós;
Exercício 03
- Revisitar exercícios de
Python? - Funções anónimas (???)
- Aplicações: map, filter, reduce
Exercício 04
- Lisp (sbcl)
Exercício 05
E → T E₁
E₁ → + T E₁ | - T E₁ | λ
T → F T₁
T₁ → * F T₁ | / F T₁ | λ
F → ( E ) | N
N → D N₁
N₁ → λ | D N₁
D → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
- Verifique que a gramática acima é LL(1) e implemente uma calculadora na linha de comandos para efetuar contas simples como
2 + (3 * 4).
Exercício 06
- Melhorar
ALisP:- Incluir um gerador de números aleatórios nas funções base.
- Corrigir
atom_valuede forma a prever o tipo do valor, em vez de levantar exceções. - Tratar adequadamente as
string, delimitadas por". - Suportar
quote, de forma a suspender a valoração de uma expressão. - Mudar
ALisP.valuede forma a queTrueeFalsesejam sempre booleanos (não é o caso agora!)
- Extensões
ALisP(range start end)(fechado-aberto).(for var list instr)(native "Python expr")como?(pair key val),(update key val map),(get key map),(keys map)(fn-map fn list),(filter pred list),




















