Exercícios — Análise Sintática

Os exercícios assinalados com "✓" serão resolvidos nas aulas práticas; Os assinalados com "†" têm elevada dificuldade. Todos os restantes devem ser resolvidos pelos alunos.

Exercícios — Análise Sintática

Limpeza de uma Gramática

Exercício 01

Considere a gramática independente do contexto $G = ({S, B, C}, {a, b, c}, P, S)$ com produções $S B C \to a S ∣ b S ∣ B \to bb ∣ C ∣ λ \to c C ∣ λ$

Escreva uma expressão regular que represente a linguagem gerada por $G$ .
Construa uma gramática (essencialmente) não contraível equivalente.
Elimine as produções unitárias da gramática obtida na alínea anterior.

Exercício 02

Repita o exercício anterior para a gramática:

$G = ({S, A, B, C}, {a, b, c}, P, S)$ com produções

$S A B C \to A BC ∣ λ \to a A ∣ a \to b B ∣ A \to c C ∣ λ$
$G = ({S, A, B}, {a, b}, P, S)$ com produções

$S A B \to BS A ∣ A \to a A ∣ λ \to B ba ∣ λ$

Construa uma gramática equivalente a $G = ({S, A, B, C}, {a, b, c}, P, S)$ , com produções $S A B C \to A ∣ B ∣ C \to aa ∣ B \to bb ∣ C \to cc ∣ A$ que não contenha produções unitárias e escreva uma expressão regular que represente a linguagem gerada por esta gramática.

Exercício 04

Construa uma gramática equivalente a $G = ({S, A, B, C, D, E, F, G}, {a, b}, P, S)$ , com produções $S A B C D E F G \to a A ∣ B D \to a A ∣ a A B ∣ a D \to a B ∣ a C ∣ BF \to B b ∣ a A C ∣ E \to b D ∣ b C ∣ b \to a B ∣ b C \to a F ∣ a G ∣ a \to a ∣ b$ sem símbolos inúteis e encontre uma expressão regular que represente a linguagem gerada por esta gramática.

Exercício 05

Construa uma gramática equivalente a $G = ({S, A, B, C}, {a, b, c}, P, S)$ , com produções $S A B C \to a A b B ∣ A BC ∣ a \to a A ∣ a \to b B c C ∣ b \to ab c$ na forma normal de Chomsky.

Exercício 06

✓ Construa uma gramática equivalente a $G = ({E, S, T}, {a, b, -}, P, E)$ , com produções $E S T \to S \to T ∣ S - T \to a ∣ b$ na forma normal de Greibach.

Exercício 07

Repita o exercício anterior para a gramática

Com produções $A B \to a A b ∣ B \to B b ∣ λ$
Com produções $S A B \to A ∣ B \to AAA ∣ a ∣ B \to BB b ∣ b$

Gramáticas LL(k)

Exercício 08

Calcule os símbolos diretores e determine se as seguintes gramáticas são $LL (1)$ :

$G_{1} = ({S, A, B}, {a, b, c, #}, {S \to A B #, A \to a A b ∣ B, B \to a B c ∣ λ}, S)$
$G_{2} = ({S, A, B, C}, {a, b, c, d, #}, {S \to A BC #, A \to a A ∣ λ, B \to b B c ∣ λ, C \to c A ∣ d B ∣ λ}, S)$
✓ $G_{3} = ({S, A, B, C, D}, {a, b, c, d, #}, {S \to a A d #, A \to BC D, B \to b B ∣ λ, C \to c C ∣ λ, D \to b D ∣ λ}, S)$

Exercício 09

†✓ Modifique a gramática $G = ({S, A, B, C}, {a, b, c, #}, P, S)$ de modo a obter uma gramática $LL (1)$ equivalente. As produções de $G$ são: $S A B \to A # \to a B ∣ A b ∣ A c \to b B c ∣ λ$ Sugestão: Comece por determinar $L (G)$ .

Exercício 10

Repita o exercício anterior para a gramática $S A B C \to a A # ∣ ab B # ∣ ab c C # \to a A ∣ λ \to b B ∣ λ \to C c ∣ λ$

Exercício 11

Defina uma gramática $LL (1)$ que gere a linguagem das expressões aritméticas com subtração, multiplicação e parêntesis. (Use o símbolo $n$ para representar os inteiros.)

Gramáticas LR(0)

Exercício 12

Determine os $contexto- L R (0)$ da gramática com produções

$S A B \to a A ∣ b B \to ab A ∣ b B \to b B c ∣ b c$

$S A B \to a A ∣ a B \to a A b ∣ b \to b B a ∣ b$

Exercício 13

✓ Considere a gramática $G = ({S, A, B}, {a, b, #}, {S \to a B A #, A \to b ∣ a B, B \to a ∣ b B}, S)$ .

Construa o autómato dos itens válidos de $G$ .
Diga, justificando, se $G$ é $L R (0)$ .
Construa a tabela de análise sintática para $G$ .
Defina o autómato de pilha reconhecedor $L R (0)$ para $G$ .

Exercício 14

Repita as duas primeiras alíneas do exercício anterior para a gramática $G = ({S, A, B}, {a, b, #}, {S \to a A # ∣ A B #, A \to a A b ∣ b, B \to ab ∣ b}, S)$ Se concluir que a gramática não é $L R (0)$ , enumere os conflitos encontrados.

Exercício 15

Repita o exercício anterior para a gramática $G = ({X, Y, Z}, {0, 1, #}, {X \to Z Y # ∣ 1 Y Z #, Y \to 0 Y ∣ λ, Z \to Z 1 ∣ 1}, X) .$

Gramáticas LR(1)

Exercício 16

✓ Considere a gramática $G = ({S, A, B}, {a, b}, P, S)$ , com o conjunto de produções: $S A B \to A B \to a A ∣ λ \to B b ∣ λ$

Construa o autómato dos itens $L R (1)$ válidos de $G$ .
Diga, justificando, se $G$ é $L R (1)$ .
Construa o autómato amalgamado e diga, justificando, se $G$ é $L A L R (1)$ .
Construa a tabela de análise sintática $L R (1)$ para $G$ .
Com base no autómato dos itens válidos de $G$ , defina o autómato de pilha reconhecedor $L R (1)$ .
Construa a computação do autómato de pilha para a palavra $aabb$ .

Resolução em Banda Desenhada

AIV	TAS	APR

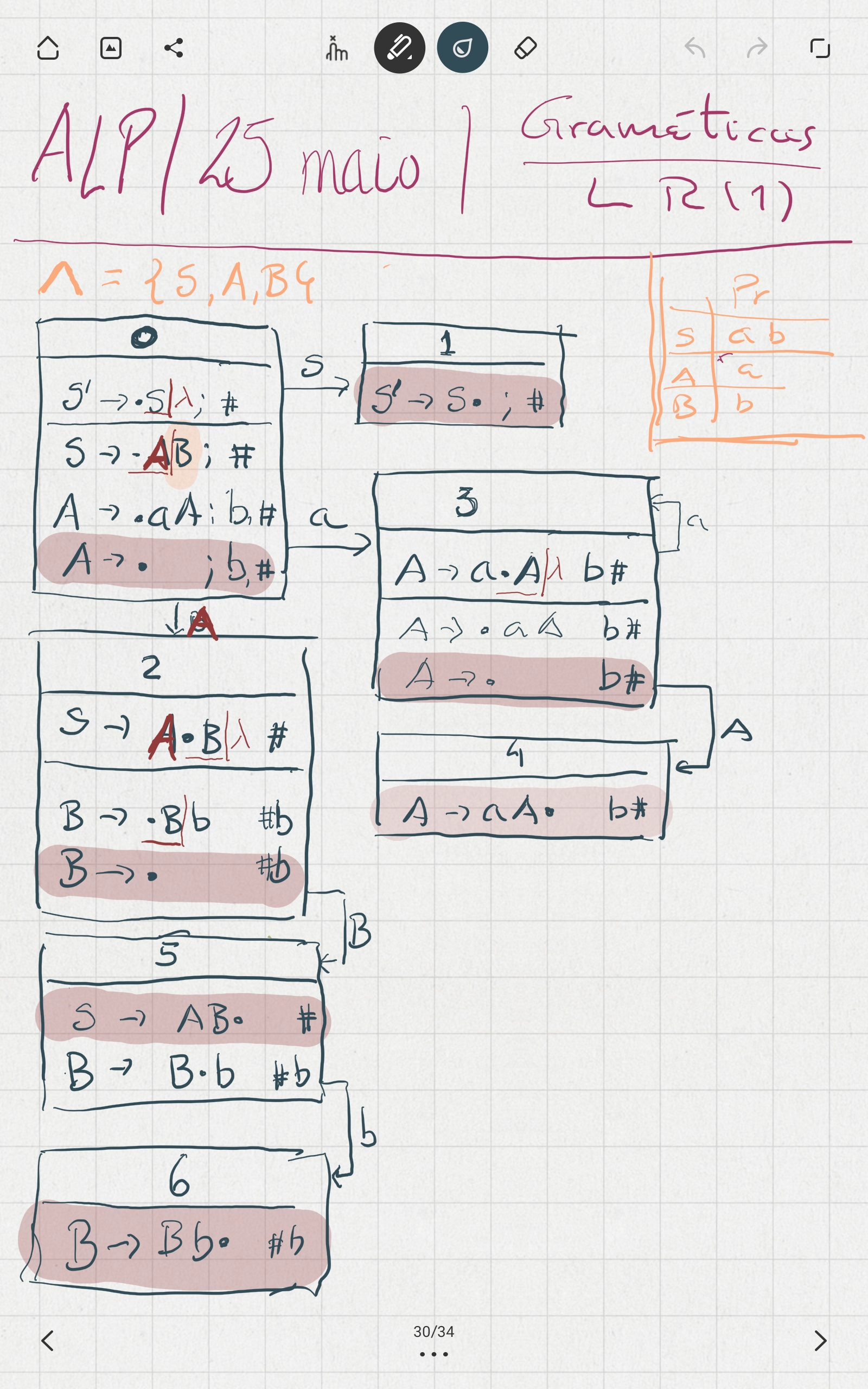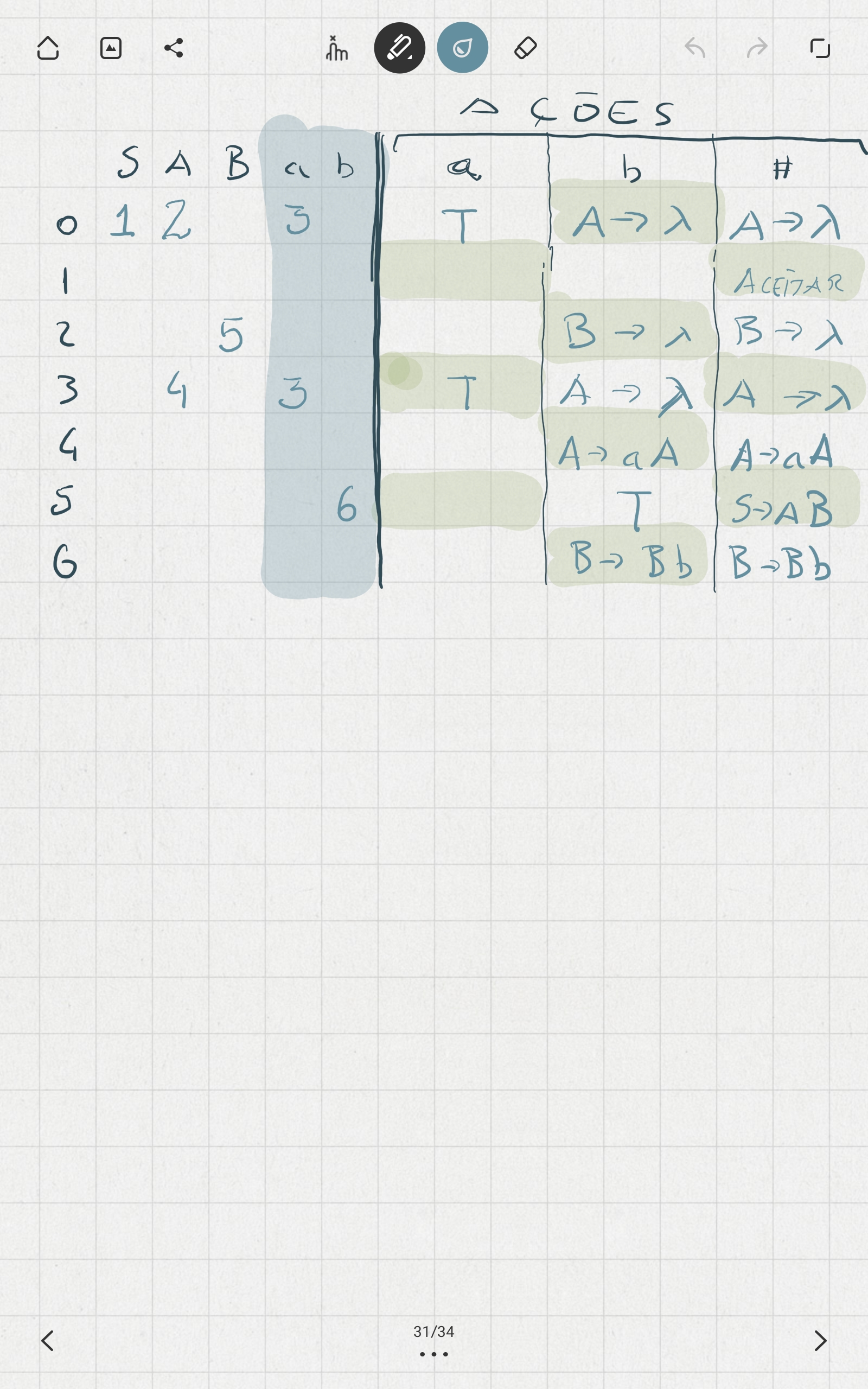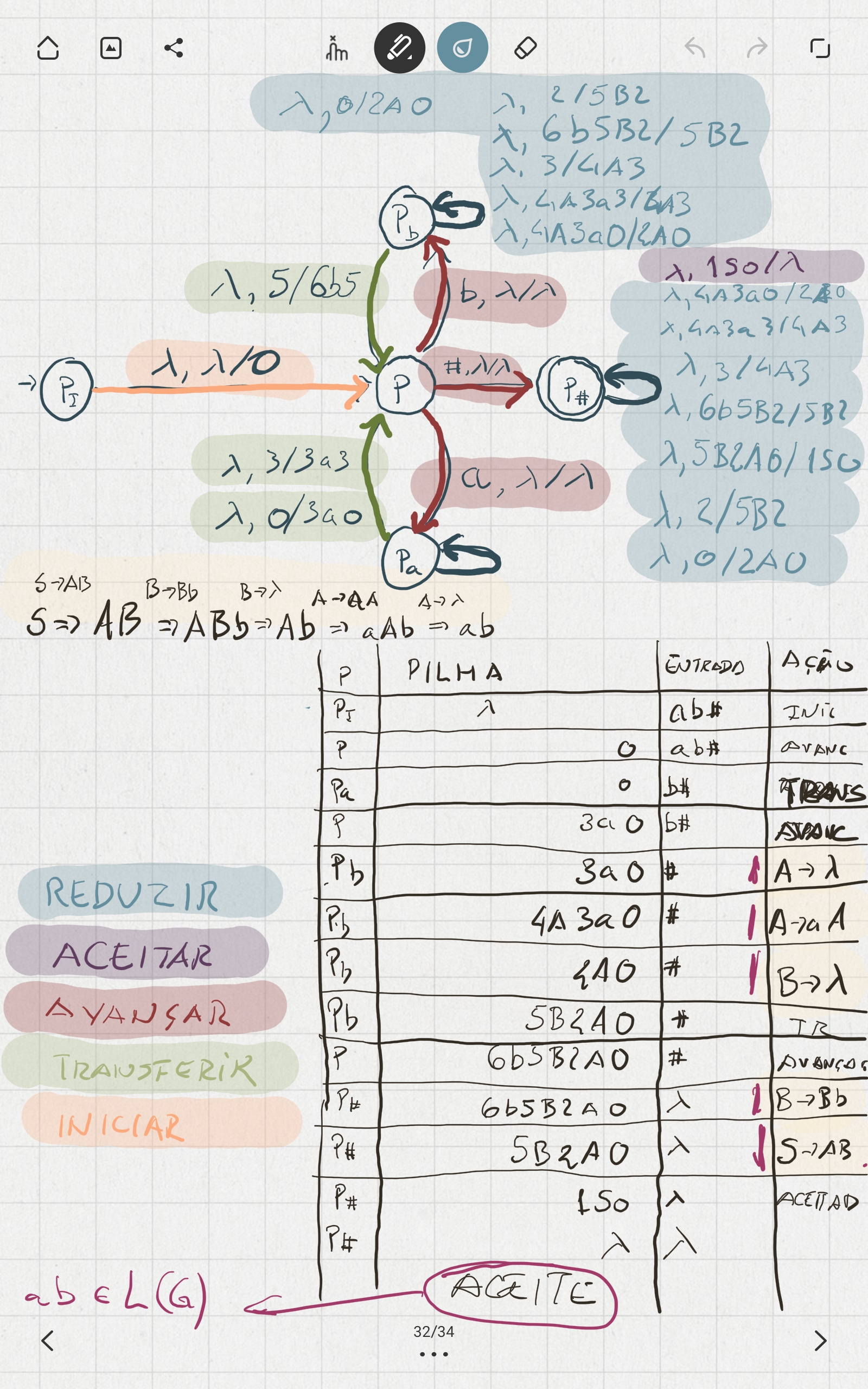Exercício 17

✓ Repita o exercício anterior com a gramática $G = ({S, A, B}, {a, b}, P, S)$ , com o conjunto de produções: $S A B \to A B A \to A a ∣ λ \to b B ∣ b$

Exercício 18

✓ Repita as primeiras 4 alíneas do exercício anterior com a gramática $G = ({S}, {a}, P, S)$ , com o conjunto de produções: $S \to a S a ∣ λ$ (Se $G$ não é $L R (1)$ , não faça as alíneas que não se aplicam.)

Exercício 19

Repita o exercício anterior com as gramáticas

$G = ({S, E, F}, {w, x, y, z}, P, S)$ , com o conjunto de produções:

$S E F \to E x ∣ y Ew ∣ Fw ∣ y F x \to z \to z$

$G = ({S, C}, {c, d}, P, S)$ , com o conjunto de produções:

$S C \to CC \to c C ∣ d$

$G = ({E, T}, {i, +, (,)}, P, E)$ , com o conjunto de produções:

$E T \to E + T ∣ T \to i ∣ (E)$

Implementação

As indicações gerais para os exercícios de implementação são válidas aqui.

Uma biblioteca para Grafos Orientados, com Pesquisas

Para este grupo de exercícios pode usar, entre outros, os grafos indicados a seguir.

# Grafos para testar as implementações.
simples = [
  (0, 2),
  (1, 3),
  (2, 0),
  (3, 1),
]

cubo = [
  (0, 1), (0, 4),
  (1, 2), (1, 5),
  (2, 3), (2, 6),
  (3, 0), (3, 7),
  (4, 5), (5, 6), (6, 7), (7, 4)
]

cubo_inclinado = [
  (0, 1), (0, 3), (0, 4),
  (1, 2), (1, 5),
  (2, 6),
  (3, 7),
  (4, 5), (4, 7),
  (5, 6),
  (7, 6)
]

Represente. Uma aresta orientada $a \to b$ por um tuplo (a, b).
Represente. Um Grafo (orientado) por uma lista de arestas.
Implemente. A função nodes(graph) que devolve o conjunto do vértices do grafo.
Implemente. A função children(graph, node) que devolve o conjunto dos filhos do vértice node.
Implemente. A função parents(graph, node) que devolve o conjunto dos pais do vértice node.
Implemente. A função is_path(graph, path) que testa se path é um caminho no grafo graph. Um caminho é uma lista de vértices em que dois consecutivos estão ligados por uma aresta.
Implemente. A função has_loop(graph, path) que testa se path tem algum ciclo no grafo graph. Um ciclo é um caminho que começa e termina no mesmo vértice.
Implemente. A função search(graph, a, b) de acordo com os apontamentos teóricos. Considere uma variante em que as funções expand e join são passadas como argumentos opcionais. Verifique o que acontece se não controlar os vértices visitados.
Teste. Pesquisas ascendentes, descendentes, em largura e em profundidade.

Uma biblioteca para Árvores, com Pesquisas

Represente. Um nó/vértice é representado pela estrutura Node com atributos:
- value: Qualquer "coisa" que pode estar no nó.
  - Obs. nem todas as linguagens permitem isto facilmente. Em python e kotlin, por exemplo, é direto.
- children: Uma lista de Node.
  - Obs. esta recursividade também levanta problemas em algumas linguagens. Por exemplo, em rust terá de fazer algo do género Vec<Box<Node>>. Em python não terá qualquer dificuldade.
Implemente. A função leaf(value) cria uma folha (isto é, um nó sem filhos).
Implemente. A função binop(op, lhs, rhs) cria um nó com value op e dois filhos: lhs e rhs. Considere variantes em que lhs, rhs são Node ou são um tipo qualquer.
Implemente. A função node(value, children) aceita um número variável de valores em children. Por exemplo node("plus", 3, 4, 5) e não node("plus", [3, 4, 5]).
Escrita. A função repr(node) devolve uma string com a representação de uma árvore, um valor por linha. Indente os descendentes. Por exemplo:

plus
- 3
- times
  - 4
  - 5

Alternativamente, as árvores podem ser representadas por listas de listas. Por exemplo:

("plus" 3 ("times" 4 5)) =
("plus"
    3
    ("times"
        4
        5
))

Desta forma, em geral n = Node(value, children) define a lista [n.value] + CHILDREN em que CHILDREN é a lista das representações dos nós em n.children.

N.B. usando a notação do python, tree.children = tree[1:] e tree.value= tree[0]. Além disso, a representação das folhas é o próprio valor, não uma lista.

Pesquisa:

Implemente. A função search para pesquisas (em profundidade e em largura).
- Começe com pesquisas por valor exato: Por exemplo, search(tree, value) procura em tree um nó n tal que n.value == value. No caso de existir um nó nessas condições, devolve o caminho para esse nó.

Caminhos para nós descendentes. Por exemplo, se tree for o exemplo acima, o caminho para chegar ao nó com o valor 4 é a lista [1, 0] porque começando na raiz (o nó com valor plus) escolhe-se o filho na posição 1 (o nó com valor times e filhos [4, 5]) e, desse nó escolheu-se o filho na posição 0; Isto é, o caminho [0, 1] indicas os indices dos filhos escolhidos, quando se "desce" a árvore.

O caminho para chegar ao valor 5 seria [1, 1] e para chegar a times seria apenas [1]. Finalmente [0] dá o valor 3 e o caminho [] leva ao valor ... (exercício).

Implemente. A função subtree(tree, path) devolve o nó que corresponde ao caminho path. Se não existe tal nó, devolve "não definido".
Generalize. Há várias generalizações interessantes:
- Use um predicado em vez de um valor. Por exemplo, para encontrar um nó com o valor par: tree.searchD(lamba x: x.value % 2 == 0).
- Encontre todas as ocorrências em vez de apenas uma. Ou encontre até n ocorrências. Por exemplo: tree.search(lambda x: len(x.children) > 2, n=42) para encontrar 42 nós com mais do que dois filhos. Convencione que, se n for "não definido" procura todas as ocorrências.
  - A pesquisa de todas as soluções também tem um tratamento interessante que consiste em implementar a pesquisa como uma stream que produz um novo nó sempre que solicitada. No caso do python pode usar yield. Noutras linguagens, ymmv.
- Implemente outras estratégias de pesquisa. Por exemplo a Iterative deepening depth-first, é uma forma melhorada de pesquisas em profundidade.

Analisadores LL(1)

Considere a GIC

$E x p r \to a t o m ∣ (S e q) S e q \to λ ∣ E x p r S e q$ em que os terminais são $a t o m, ($ e $)$ .

Verifique (manualmente) se é LL(1) e, nesse caso, implemente um analisador sintático LL(1). A função parse(s) tem como argumento a string s e devolve uma árvore.

Comece por separar (tokenize) a palavra numa lista de símbolos.
Precisa de um "contexto" de processamento com:
1. O símbolo seguinte: next.
2. A lista dos símbolos que faltam processar.
3. A função consume(symbol).
Processe a lista de tokens usando as funções proc_Expr(token, tokens, tree) e proc_Seq(token, tokens, tree):
- token é o símbolo de avanço.
- tokens são os restantes símbolos da palavras (incluindo token).
- tree é a árvore que resulta do processamento da função.
Vai precisar de funções auxiliares como consume(token, tokens)

Uma biblioteca para GIC LL(1)

Se resolver sozinho estas alíneas ganha o direito de se gabar nas aulas de ALP durante uma semana. E o dever de ajudar os seus colegas.

‡ Implemente. O método firsts() que devolve um mapa do tipo symbol: set<symbol> que associa a cada símbolo (variável ou terminal) da gramática o conjunto dos seu primeiros.

‡ Implemente. O método follow() que devolve um mapa do tipo symbol: set<symbol> que associa a cada símbolo (variável ou terminal) da gramática o conjunto dos seu seguintes.

Análise Sintática LL(1)

Implemente. O método firsts_of(symbol) devolve o conjunto dos primeiros de symbol.
Implemente. O método follow_of(symbol) devolve o conjunto dos seguintes de symbol.
Implemente. O método directors(rule) devolve o conjunto de diretores da regra rule.
Teste. O método is_LL1() testa se grammar é LL(1).

Uma biblioteca para GIC LR

Itens

Represente. Um item LR(1) é representado pela classe Item com atributos:
- rule uma regra.
- lookahead uma lista de símbolos.
- position um inteiro, que indica a posição do "ponto".
Teste. O método is_complete() testa se o item é completo.
Implemente. O método active_prefix() devolve o prefixo até à posição do "ponto".
Implemente. O método active_symbol() devolve o símbolo imediatamente a seguir ao ponto se o item não for completo e "não definido" caso contrário.
Implemente. O método active_suffix() devolve o sufixo desde a posição a seguir ao "ponto".
- N.B: active_prefix + active_symbol + active_suffix deve reconstruir o lado direito da produção.
Implemente. O método transition(symbol) devolve o item que resulta de "ler" symbol. Isto é, se symbol == active_symbol no novo item o "ponto" avança uma posição. Caso contrário devolve "não definido".
Escrita. O método __repr__() devolve uma string da forma C〈V → P · A S ⎅ L〉 em que:
- C é "'★'" quando o item é completo e vazia ('') caso contrário.
- V é o lado esquerdo da produção.
- P, A e S são o prefixo, símbolo e sufixo ativos.
- L é a lista dos símbolos de avanço, separados por espaços. Se for vazia, use ∅.
- Use mesmo os símbolos indicados: ★〈→·⎅∅〉

Análise Sintática, Autómato dos Itens Válidos

Na biblioteca para os AFD estes são construídos com uma lista de transições, o estado inicial e uma lista de estados finais. Além disso, os estados são inteiros.

Mas, na construção do Autómato dos Itens Válidos os estados "contêm" conjuntos de itens. Esta diferença é resolvida mantendo uma associação (mapa, dicionário) dos estados do AFD para os conjuntos de itens. A vantagem é que não é preciso mudar a implementação dos AFD. A desvantagem é que se torna necessário fazer alguma "manutenção" dessa associação.

Representação. Uma classe VIA com atributos:
- grammar a gramática.
- fsa o autómato dos itens válidos calculado para grammar.
- states a associação dos estados do autómato para os conjuntos de itens.
- table a tabela de análise sintática, uma associação dos estados+avanços do autómato para reduções/transferências.
- phase um inteiro (ou enum) para marcar a fase de processamento: INITIAL = 0 → GRAMMAR_OK → START_OK → VIA_OK → TABLE_OK. Se algum destes passos correr mal → ERROR.
Construção. O método make_VIA(). Se grammar.is_valid() incrementa phase.
† Implemente. O método calc_startCore() que calcula o núcleo do estado inicial de via. Devolve um conjunto de itens.
† Implemente. O método close(itens) que calcula o fecho de um conjunto de itens. Devolve um conjunto de itens.
Implemente. O método build_START() que calcula o estado inicial de via. Se correr bem incrementa phase.

Se resolver sozinho todas as alíneas seguintes ganha o dever de ajudar os seus colegas. E o direito de se gabar nas aulas de ALP durante uma semana.

† Implemente. O método build_FSA() processa grammar para definir o autómato fsa, a associação states e is_built. Se correr bem incrementa phase.
† Implemente. O método build_TABLE() processa grammar, fsa e states para definir table. Se correr bem incrementa phase.

† Implemente. O método derive(word) para encontrar uma derivação de word pela gramática via.grammar. N.B. não é necessário implementar autómatos de pilha.
† Implemente. O método derivation_tree(word) que calcula a Árvore de Derivação de word.
Controlo. Use phase para evitar computações repetidas, precoces ou desnecessárias. Por exemplo, suponha que houve um erro a calcular o estado inicial. Então quando "chama" build_FSA deve evitar calcular o AFD. Por outro lado, se já calculou fsa com sucesso e "acidentalmente" chama build_FSA não há razão para repetir esses cálculos.
- Também pode usar phase para implementar cálculos build--- "inteligentes" (Ah! Ah!). Suponha que "chama" build_TABLE mas phase < VIA_OK. Nesse ponto pode chamar build_VIA que por sua vez faz uma análise semelhante.

Autómatos e Linguagens de Programação