Seguinte: Área da superfície esférica Acima: Arquimedes de Siracusa, 287-212 Anterior: Um teorema sobre a
Aquele que ficou conhecido como o Método de Arquimedes vem dos seus estudos da física. Foi finalmente compreendido há cerca de um século, depois de ter sido encontrado num livro de uma bilioteca de Constantinopla (hoje Istambul) pelo estudioso dinamarquês J. L. Heiberg. Este reconheceu o autor que subjazia num palimpsesto (um escrito de missas de monges bizantinos num suporte de papiro ou pele já utilizado, depois de raspado e lavado). O ``palimpsesto de Arquimedes'' contém muitas páginas de resultados para sempre julgados perdidos, uns que não chegaram a ser apagados e outros legíveis por recursos técnicos, incluindo o texto do agora famoso ``Stomachion'', um jogo inventado pelo mestre.
Vejamos uma aplicação do Método.
Recorde-se, para o que segue, que o volume do cone em relação ao cilindro com a mesma base e altura estavam já calculados. Com efeito, aparecem nos Elementos de Euclides, tomando essa razão o valor de ![]() . Segundo [3], Arquimedes atribui o resultado ao célebre filósofo atomista Demócrito. Sobre o volume das esferas, o caso é mais complicado.
. Segundo [3], Arquimedes atribui o resultado ao célebre filósofo atomista Demócrito. Sobre o volume das esferas, o caso é mais complicado.
O volume da esfera é ![]() do volume do cilindro com altura e diâmetro da base iguais ao diâmetro da esfera.
do volume do cilindro com altura e diâmetro da base iguais ao diâmetro da esfera.
O esquema representa uma secção da esfera e de um cilindro e um cone com o dobro da base dos mencionados. O ponto ![]() servirá de fulcro da balança. Passa-se uma recta (um plano paralelo ao plano da base) genérica por
servirá de fulcro da balança. Passa-se uma recta (um plano paralelo ao plano da base) genérica por ![]() . Por semelhança de triângulos,
. Por semelhança de triângulos,
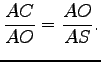 |
 |
| esfera |
cilindro pequeno esfera esfera |
Obras anteriores de Arquimedes dão-nos os enunciados do teorema acima. Mas só no Método é que ele explica como o obteve (aquele e muitos outros), defendendo ainda que o seu método mecânico lhe parecia tão bom como os demais geométricos pelos quais, ao longo da vida, por vezes em segunda ocasião havia provado os seus resultados. Cremos que um destes é o resultado sobre a parábola (teorema 1) pois são conhecidas duas demonstrações.
rpa 2007-11-14