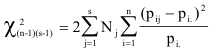
Parte VI: registo e análise dos resultados
A — Observação dos zimogramas
Os zimogramas produzidos por compostos corados eram observados imediatamente após a
diferenciação, sobre um transiluminador de luz branca, enquanto os de produtos fluorescentes eram
monitorizados periodicamente (intervalos de 15 minutos após a primeira meia hora de incubação) sob
luz ultravioleta de 315 nm.
Em todos os casos os geis eram orientados com o lado anódico para cima, e graças ao corte feito
nos cantos do lado esquerdo (cf. parte V secção A1) era possível identificar os zimogramas com o
posicionamento das amostras no passo de colocação dos aplicadores de papel de filtro (cf. parte IV
secção A3). Em geral não era difícil identificar as sucessivas amostras, mas para o caso de haver dúvidas,
nomeadamente quando havia várias amostras negativas em sucessão, comparava-se entre fatias replicadas
para fixar a ordem de cada amostra no gel.
O registo dos resultados era feito para cada actividade enzimática segundo as codificações que lhe
eram específicas (cf. “Resultados” parte II), frequentemente acompanhadas duma redução esquemática
das bandas presentes, como se exemplifica na figura 3.5.
 Figura 3.5 — Exemplos de registo de resultados no caderno de laboratório. As primeiras
duas linhas são o registo das amostras colocadas em cada gel (Sg e Sg+ são amostras de sangue,
cor. um corante alimentar) seguindo-se do lado esquerdo num esquema-resumo das posições
relativas das bandas observadas e da origem (or.) da electroforese. a) PGM. b) EST.
Figura 3.5 — Exemplos de registo de resultados no caderno de laboratório. As primeiras
duas linhas são o registo das amostras colocadas em cada gel (Sg e Sg+ são amostras de sangue,
cor. um corante alimentar) seguindo-se do lado esquerdo num esquema-resumo das posições
relativas das bandas observadas e da origem (or.) da electroforese. a) PGM. b) EST.
 Figura 3.6 — Exemplo de registo
fotográfico: electroforeses realizadas no dia 6
de Março de 2000, gel 2, DIA e MDH.
Figura 3.6 — Exemplo de registo
fotográfico: electroforeses realizadas no dia 6
de Março de 2000, gel 2, DIA e MDH.
Estes registos eram, tão brevemente quanto possível, adicionados ao ficheiro
Excel ANALISES.xls
(incluído no CD anexo ao
presente trabalho), onde
cada folha corresponde a
uma série de extracção,
exceptuando os híbridos
com uma folha àparte. Os
registos nesta folha de
cálculo eram verificados por
uma segunda pessoa,
confrontando-os com os
registos no caderno de
laboratório.
Só quando finalizada
a observação directa e
registo se decidia se havia
interesse em guardar a
imagem do zimograma em
fotografia, o que era feito
após legendagem do gel
com inscrições da data, do
sistema de separação e da
actividade enzimática
(figura 3.6).
B — Estatística
O CD anexo ao presente trabalho contém todos os resultados de tratamento de dados realizados
e o software de visualização (Columbus versão pessoal, distribuído com autorização expressa do
fabricante Oasys, http://www.oasys-software.com/products/dm/columbus/).
1) Estimação
Distribuições de frequência
As distribuições de frequência obtiveram-se com base no ficheiro Quattro Pro zimogramas.qpw,
adaptado a partir do ANALISES.xls, no qual todas as amostras (2430 no total, tendo-se incluído
observações mais antigas que não figuravam no ANALISES.xls) foram ordenadas pelas séries
respectivas. Esta folha de cálculo foi convertida numa tabela Paradox (zimogramas.db), à qual se
adicionou um campo chamado “freq”, com valor 0 por defeito, para a apresentação dos resultados. A
partir desta tabela, com programa Corel Paradox 9, definiram-se filtros e algoritmos de consulta (queries)
no sentido de classificar as amostras segundo os mais diversos critérios, produzindo-se subtabelas
(azinheiras.db, sobreiros.db, etc.) onde outros filtros e quesitos podiam ser aplicados. Destas
distribuições de frequência podiam calcular-se as estimativas mais diversas.
Exemplos de ficheiros SQL utilizados nestas operações, com comentários sobre o seu conteúdo,
encontram-se no Apêndice IV secção B.
Potencial de cada marcador isoenzimático
No presente estudo a descrição do potencial de cada marcador genético em termos de detecção de
hibridismo ou introgressão é baseada em cálculos de especificidade e sensibilidade apenas para as
actividades que foram incluídas em análises em larga escala. A probabilidade dum marcador produzir
uma classificação incorrecta tanto pode constituir uma perda de especificidade como de sensibilidade,
dependendo do ponto de vista com que se utiliza esse marcador. No presente estudo, usou-se na prática
o ponto de vista da classificação de cada indivíduo como sendo diferente de sobreiro ou não. Assim, a
presença dum zimograma de híbrido ou de azinheira é um “positivo”, e a sua ausência um “negativo”.
Todos os indivíduos que sejam sobreiros e apresentem um tal zimograma são falsos positivos (e a sua
proporção estima a perda de especificidade do marcador em causa em relação aos 100%), e todos os que
não sejam e não apresentem esse zimograma são falsos negativos (perda de sensibilidade).
Probabilidade de hibridismo
O cálculo das probabilidades de hibridismo nas parcelas mistas, tendo em conta que essas
probabilidades eram presumivelmente baixas para não ser detectado nenhum híbrido de 1ª geração, usou-se o modelo de Poisson
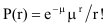 , em que r é o número de ocorrências do evento para o qual
se calcula a probabilidade e μ o número médio dessas ocorrências. Considerando r = 0 (não haver
nenhuma ocorrência), e μ = NP, sendo P o valor a deteminar e N o número de indivíduos observados,
P(0) = e–NP, estimando-se P pela desigualdade 1 – e–NP < α, tal que a probabilidade de haver 1 ou mais
ocorrências é majorada por α. Obtém-se assim P < –loge(1 – α)/N.
, em que r é o número de ocorrências do evento para o qual
se calcula a probabilidade e μ o número médio dessas ocorrências. Considerando r = 0 (não haver
nenhuma ocorrência), e μ = NP, sendo P o valor a deteminar e N o número de indivíduos observados,
P(0) = e–NP, estimando-se P pela desigualdade 1 – e–NP < α, tal que a probabilidade de haver 1 ou mais
ocorrências é majorada por α. Obtém-se assim P < –loge(1 – α)/N.
2) Testes de hipóteses
Tabelas de contingência
Para determinar se as parcelas mistas poderiam ser consideradas em conjunto, ou seja, se para cada
espécie elas constituem uma só população, usou-se o método das tabelas de contingência para o número
de alelos observados, em comparação com os esperados na hipótese de aplicarem-se as mesmas
frequências a todas.
Na formulação do correspondente teste χ2, trata-se de comparar as frequências pij (alelos i, parcelas
j) com as frequências pi · do conjunto das parcelas, tal que (2Njpij–2Njpi ·)2/(2Njpi ·) para cada parcela, com
Nj a representar a dimensão da amostragem (número de adultos) na parcela j. O número de graus de
liberdade é dado pela diferença entre o número n×s de comparações (n alelos, s parcelas) e o número de
parâmetros requeridos para estimar as frequências esperadas, (n–1) + s. Deste modo, obtém-se a fórmula
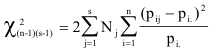 .
.
Outra tabela de contingência foi construída para examinar se havia independência de associação,
entre gâmetas portadores de alelos de sobreiro e de azinheira, isto é, entre as 4 combinações ♀ sobreiro
× ♂ sobreiro, ♀ sobreiro × ♂ azinheira, ♀ azinheira × ♂ sobreiro, e ♀ azinheira × ♂ azinheira. Neste caso
a estatística χ2 tem apenas 1 grau de liberdade, sendo necessário aplicar a correcção de Yates (subtracção
de 0,5 ao valor absoluto do desvio entre frequência observada e esperada).
Modelos populacionais
Usou-se o cálculo da estatística χ2 para o teste à hipótese de que as frequências observadas se
desviavam das esperadas devido ao acaso, para dois modelos: a 1ª Lei de Mendel, onde se prevê que os
alelos num locus heterozigótico segreguem homogeneamente (isto é, ½ + ½) pelos gâmetas, e a
distribuição de Hardy-Weinberg, que a cada frequência dum genótipo homozigótico faz corresponder
o quadrado da frequência do respectivo alelo, e à dum heterozigótico o dobro do produto entre as
frequências dos dois alelos relevantes. No segundo modelo o número de graus de liberdade é igual ao
número de comparações menos o número de frequências alélicas necessárias para calcular os valores do
modelo enquanto no primeiro é 1. Nos casos com 1 grau de liberdade, aplicou-se a correcção de Yates
descrita na secção precedente.
3) Estimadores genéticos
Para cada locus com n alelos de frequências xi, i = 1, ..., n, e na comparação entre as parcelas k
= 1, ..., L, os parâmetros estimados foram:
Identidades genéticas de Nei e GST
Para cada par de populações A e B, obtêm-se identidades genéticas jA = Σi (xiA)2, jB = Σi (xiB)2 e jAB
= Σi (xiAxiB), e a identidade intrapopulacional média JS = Σk (jk)/L, donde se tira HS = 1– JS (nota-se ainda
que (jA)–1 é o número efectivo de alelos nesse locus, Ae, para a população A). Entre todos os pares de
povoamentos k e k' calcula-se a diferenciação entre povoamentos DST = (ΣDkk')/(L)2, com Dkk' = ½(jk +
jk') – jkk' (note-se que Dkk' = Dk' k, portanto cada valor numérico é representado 2 vezes no numerador de
DST). Obtém-se assim o coeficiente de diversidade genética GST = DST/(HS + DST) [Nei 1973, 1987, 1997].
Estatísticas de Gregorius e colaboradores
A partir da diversidade genética ν = [Σi(xi)2]–1, idêntica ao número efectivo de alelos Ae, obtém-se
a diferenciação total no povoamento δT = N(1 – 1/ν)/(N – 1), sendo N o número de indivíduos
observados. Note-se o paralelismo entre δT para uma parcela e HS para o conjunto de parcelas.
A diferenciação de cada povoamento j em relação aos restantes, Dj = ½Σi |xij – xi .|, em que o
segundo membro do módulo, xi . , é a média aritmética das frequências xi nos restantes L – 1
povoamentos. A estatística δ é a média dos L valores Dj, ponderada ou não pela dimensão de cada
população, para servir de referência aos valores Dj [Hattemer 1991].
Estatísticas de Wright (modelo das ilhas)
O coeficiente de fixação FIT = 1 – Ho/He, em que Ho é a frequência (relativa) observada de
heterozigóticos no conjunto dos povoamentos e He = 1 – Σ(xi)2, também referente ao conjunto dos
povoamentos [Wright 1969]. A relação F = 1/(2Ne) para o cálculo de Ne (tamanho efectivo da população)
aplica-se apenas numa situação de neutralidade. Adicionalmente, o valor de referência de F é 0 apenas
se as distribuições de frequência nos gâmetas masculinos e femininos forem idênticas; caso haja
diferenças Δxi entre as frequências nos gâmetas masculinos e femininos, o valor de referência Fesp para
FIT é negativo e dependente do valor dessas diferenças (Apêndice II-C), pelo que a estimativa de Ne
refere-se à diferença ΔF entre o valor observado de FIT e o Fesp.
Coeficiente de fixação FIS = 1 – LHo/Σk Hek, isto é, substituindo o He na fórmula de FIT pela média
aritmética dos He de cada povoamento k. Para que esta estatística seja credível, é necessário assumir um
Ne constante para todos os povoamentos e L grande [Nei 1987, 1997].
FST = (FIT – FIS)/(1 – FIS) é a medida de diferenciação entre povoamentos, ou seja do efeito de
Wahlund [Wright 1965, 1969]. A partir deste valor obtém-se, assumindo que esta diferenciação é
evolutivamente neutral, Nem = (1 – FST)/(4αFST), em que α = L2/(L – 1)2 [Wright 1965, Slatkin 1995,
Berg & Hamrick 1997].
4) Cálculos
Excepto onde indicado explicitamente, todos os cálculos foram realizados com o programa Corel
Quattro Pro, versão 9, em plataforma Windows (32-bit). Cabe especial menção ao programa GENEPOP,
versão 3.4, que permite realizar testes de hipóteses e estimações definindo os intervalos de confiança
com base em cadeias de Markov [Raymond & Rousset 1995]. Os resultados do mesmo são apenas
mencionados no texto onde seja relevante, e incluem-se os valores detalhados no CD anexo.
 Figura 3.5 — Exemplos de registo de resultados no caderno de laboratório. As primeiras
duas linhas são o registo das amostras colocadas em cada gel (Sg e Sg+ são amostras de sangue,
cor. um corante alimentar) seguindo-se do lado esquerdo num esquema-resumo das posições
relativas das bandas observadas e da origem (or.) da electroforese. a) PGM. b) EST.
Figura 3.5 — Exemplos de registo de resultados no caderno de laboratório. As primeiras
duas linhas são o registo das amostras colocadas em cada gel (Sg e Sg+ são amostras de sangue,
cor. um corante alimentar) seguindo-se do lado esquerdo num esquema-resumo das posições
relativas das bandas observadas e da origem (or.) da electroforese. a) PGM. b) EST.